Les éléments passifs : résistance, condensateur et bobine

Dans ce nouvel article de la série « théorie pour néophytes », nous allons nous intéresser aux 3 composants linéaires passifs que sont la résistance, le condensateur et la bobine. Par passif, on veut dire que ces composants consomment ou emmagasine de l’énergie.

Il y a un peu de maths, mais amenés en douceur. À la fin je fais un petit aparté sur la signification du mot linéarité.

Sommaire

1 Éléments passifs non réactifs

Il s’agit de la résistance, de valeur R.

La valeur de la résistance (en ohms de symbole $\Omega$ ) est associée à la perte d’énergie des porteurs de charge (les électrons) dû au matériel que constitue la résistance.

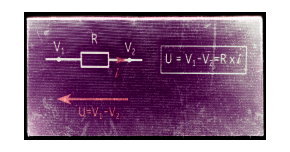
Cette perte d’énergie crée une chute de tension d’autant plus importante que R est grand, comme l’indique le schéma suivant :

Symbole de la résistance. Ses bornes sont à un potentiel différent V1 et V2. La tension ou différence de potentiel à ses bornes est donc U= V1- V2. La loi d'Ohm donnant la relation entre tension et courant est une loi de proportionnalité, ayant pour coefficient de proportionnalité R. — Symbole de la résistance. Ses bornes sont à un potentiel différent V₁ et V₂. La tension ou différence de potentiel à ses bornes est donc U= V₁– V₂. La loi d’Ohm donnant la relation entre tension et courant est une loi de proportionnalité, ayant pour coefficient de proportionnalité R.

Dans un circuit, les différents points ou nœuds qui le constituent sont à un potentiel (ou tension) différent. On peut comparer cela à une carte où les montagnes ont des hauteurs différentes. Entre les diverses montagnes on a des différences d’altitude (vous pouvez lire cet article pour plus de détails).

Et bien dans le circuit c’est pareil, aux bornes de chaque composants nous avons des potentiels différents. Aux bornes de la résistance illustrée ci-dessus, une des borne est au potentiel V₁, l’autre est au potentiel V₂.

La tension aux bornes de la résistance, ou chute de potentiel est U= V₁ – V₂.

Cette chute de tension est d’autant plus grande que la résistance R est grande. On a même une relation de proportionnalité : la tension est proportionnelle au courant qui passe à travers la résistance. Plus R est grand, plus U est grand. On appelle cette relation la loi d’ohms :

$\boxed{U = R\times i}$

Mentionnons également que la puissance P dissipée (sous forme de chaleur) par la résistance est :

$\boxed{P = U \times i = R \times i^2 = \frac{U^2}{R}}$

où nous avons déduit les deux autres relations en remplaçant $U=R\times i$ et $i=\frac{U}{R}$ .

2 Éléments passifs réactifs

Il s’agit du condensateur et de la bobine.

2.1 Le condensateur

Le condensateur est formé de deux plaques métalliques séparées par un isolant. En voilà plusieurs modèles :

Différents modèles de condensateurs. Par Eric Schrader from San Francisco, CA, United States — 12739s, CC BY-SA 2.0, https://commons.wikimedia.org/w/index.php?curid=37625896 — Différents modèles de condensateurs.
Par Eric Schrader from San Francisco, CA, United States — 12739s, CC BY-SA 2.0, https://commons.wikimedia.org/w/index.php?curid=37625896

Lorsqu’on met le condensateur en contact avec un générateur, il va se charger, c’est-à-dire qu’il va emmagasiner des charges négatives (des électrons) sur une des électrodes, en quantité q. L’autre électrode va libérer la même quantité d’électrons et se charger positivement. Cette différence de charge de part et d’autre de l’isolant crée une différence de potentiel aux bornes du condensateur :

Symbole du condensateur. Lorsque le condensateur emmagasine des charges q, une différence de potentiel U apparaît à ses bornes. Le courant i est égal à la variation de la charge q dans le condensateur avec le temps. — Symbole du condensateur, de capacité C. Lorsque le condensateur emmagasine des charges q, une différence de potentiel U apparaît à ses bornes. Le courant i est égal à la variation de la charge q dans le condensateur avec le temps.

Le condensateur est caractérisé par sa capacité C, qui représente la quantité de charge qu’il peut emmagasiner.

Les personnes qui ont lu cet article ont aussi lu : Micro de guitare électrique et perte d'aigus

Il y a une relation entre la quantité de charge q emmagasinée et la tension U crée par l’apparition de charges aux bornes du condensateur:

$\boxed{q=C \times U}$

On voit donc que pour une capacité donnée, plus la charge stockée q dans le condensateur est grande, plus la tension U générée à ses bornes sera grande.

On voit aussi que pour une tension U fixe (lorsque le condensateur est complètement chargé), plus la capacité du condensateur est grande, plus la quantité de charge stockée sera grande. La capacité, c’est un peu comme la taille d’une valise : celle-ci elle a une capacité limitée pour y mettre nos chemises.

Équation du courant

Il y a une autre équation caractéristique du condensateur, qui fait appel à la dérivée du courant i par rapport au temps et qui met donc en relation le courant électrique i, la charge q et le temps t :

$\boxed{i=\frac{dq}{dt}}$

Une dérivée… qu’est-ce que ça peut bien être…?

Je ne vais pas insister ici, vous pouvez aller consulter cet article sur une explication basique de ce que sont les les dérivées si vous êtes curieux.

Mais pour faire simple, la dérivée, c’est la variation de la fonction. Par exemple, si le mois prochain vous gagnez plus que ce mois-ci, la variation est positive. Si vous gagnez moins, la variation est négative. La dérivée nous donne aussi la quantité, c’est à dire si vous avez gagné beaucoup plus ou un peu plus.

L’équation du courant donc…

Revenons à l’équation précédente qui dit que le courant i est la dérivée de la charge q par rapport au temps t.

q est la quantité de charge, on peut aussi dire que c’est la quantité d’électrons, que vous pouvez imaginer comme étant des particules. La variation de la quantité de charge ou d’électron, c’est comme la circulation routière finalement. S’il y a beaucoup de voitures qui passent par seconde, il y a beaucoup de circulation.

Par conséquent, l’équation précédente nous dit que le courant i c’est la circulation d’électrons : le nombre d’électrons qui passent par seconde. Ceci est donc valable pour le condensateur, mais partout en électronique. Dès qu’il y a mouvement d’électrons, il y a courant électrique, logique non ?

Mais pourquoi on s’embête avec la dérivée ? Pourquoi on ne dit pas que i=q/t au lieu de i=dq/dt??

C’est parce que la charge q ne varie pas linéairement avec le temps, on n’a pas une relation de proportionnalité du type q=i x t (équivalent à dire i=q/t) comme la loi d’Ohms vue plus haut par exemple. Mais nous allons revenir à la notion de linéarité dans la 3e partie de cet article, ne vous inquiétez pas !

Les personnes qui ont lu cet article ont aussi lu : Comment fabriquer rapidement vos pédales d’effet pour guitare électrique

Relation courant-tension

En combinant les 2 équations que nous avons vu pour le condensateur, on trouve la relation suivante entre le courant qui « passe » à travers le condensateur et la tension à ses bornes :

$\boxed{i=\frac{dq}{dt} = \frac{d(C\times U)}{dt} =C \frac{dU}{dt} }$

Bon, là c’est sûr, il faut savoir manier l’opérateur dérivée. $\frac{dU}{dt}$ signifie variation de la tension avec le temps.

J’ai mis cette équation car elle nous montre quand même quelque chose d’intéressant : lorsque la variation de tension avec le temps est nulle (autrement dit lorsque la tension est constante), le courant est nul. Le condensateur bloque donc les tensions constantes ou qui varient très lentement. Il se comporte donc comme un fil ouvert pour les basses fréquences et un fil fermé pour les hautes fréquences (lisez cet article si vous voulez une ilustration plus poussée).

2.2 La bobine

Avec la bobine, il y a une histoire de magnétisme. Si un conducteur est enroulé sous forme de spires, comme dans une bobine, la circulation circulaire du courant électrique induit un champ magnétique perpendiculaire au plan du cercle.

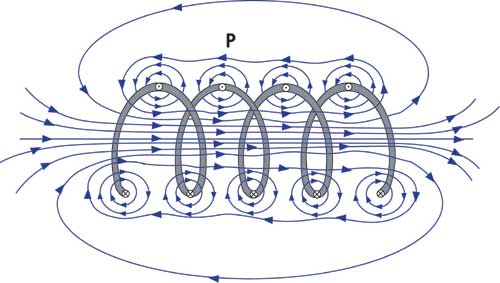
Ligne de champ magnétique autour d'une bobine traversée par un courant. https://www.nde-ed.org/EducationResources/CommunityCollege/EddyCurrents/Physics/selfinductance.htm — Ligne de champ magnétique autour d’une bobine traversée par un courant. https://www.nde-ed.org/EducationResources/CommunityCollege/EddyCurrents/Physics/selfinductance.htm

Plus il y a de courant, plus le flux magnétique va être intense. La constante de proportionnalité entre les deux est L, coefficient d’auto-induction et caractéristique de la géométrie et du matériau de la bobine. L se mesure en Henry (H).

Symbole de la bobine, d’inductance L. La variation de courant avec le temps dans la bobine crée une différence de potentiel à ses bornes.

En passant par les équations de l’électro-magnétisme dont on fera fi ici, on trouve la relation entre tension aux bornes de la bobine et courant qui la traverse :

$\boxed{U=L\frac{di}{dt}}$

Encore une dérivée… désolé. $\frac{di}{dt}$ signifie variation du courant avec le temps.

Ici nous voyons que lorsque le courant varie avec le temps, une tension apparaît aux bornes de la bobine. Sans variation de courant, la tension aux bornes de la bobine est nulle (c’est un fil). Par conséquent, par analogie à ce que l’on a vu avec le condensateur, la bobine se comporte comme un fil pour le courant continu et s’oppose aux variations de courant (en raison du champ magnétique induit donc).

3 Notion de linéarité

Ici on s’est intéressé aux 3 éléments de base qui sont primordial pour étudier tout type de circuit, même non-linéaire.

Ces éléments, résistance, condensateur et bobine sont dit linéaires, car la relation mathématique entre tension et courant fait appel à des opérateurs linéaires : proportionnalité. dérivation, intégration, etc…

Bon, la proportionnalité, tout le monde connaît non ?

Dérivation et son pendant l’intégration sont des opérateurs mathématiques plus complexes, que nous ne traiterons pas ici, comme je l’ai déjà dit plus haut. Mais ce sont des opérateurs linéaires.

Les personnes qui ont lu cet article ont aussi lu : La loi d'Ohm : comprendre simplement les fondements de l'électricité

Mais ça veut dire quoi linéaire ? Regardons la figure suivante :

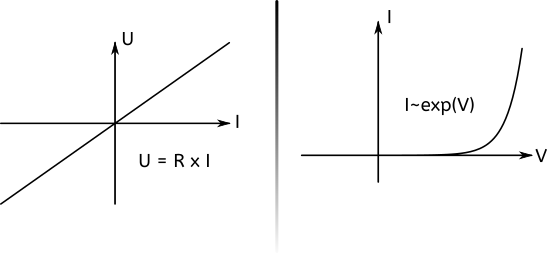
Exemple de loi linéaire à gauche (résistance R), et non linéaire à droite (diode).

C’est très facile : à gauche, c’est linéaire, à droite, c’est pas linéaire ! En électronique, en physique, dans la nature, on va pouvoir trouver des lois linéaires dans un certain contexte comme la loi d’Ohm représentée ci-dessus à gauche. Mais en général les lois sont non linéaires, comme la caractéristique courant-tension représentée à droite.

Comment s’en sort-on ? En travaillant sur une petite échelle de temps, ou d’espace, ou de tension, etc…

Par exemple, la trajectoire de la Terre n’est pas une droite, c’est une ellipse dont l’un des foyer est le Soleil. Par contre, si notre expérience dure par exemple 1h, ce temps étant très court devant sa période de 365 jours, on va considérer que la Terre a bougé sur un segment de droite. On pourra donc appliquer les équations de Newton, valables uniquement lorsque le référentiel est en mouvement rectiligne à vitesse constante (le fameux référentiel Galiléen, ça vous dit quelque chose ?).

En électronique, la majorité des composants n’est pas linéaire comme les diodes, les transistors.

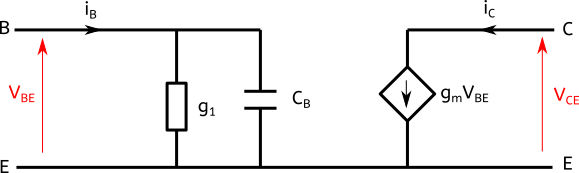
Cependant, sous certaines circonstances et en fonction de la précision voulue, on peut substituer ces composants non linéaires par un modèle de circuit linéaire contenant résistances, condensateurs, bobines et générateurs idéaux. Voici par exemple un schéma équivalent possible de transistor :

Schéma équivalent possible de transistor, faisant intervenir des éléments linéaires, dont un générateur de tension idéal dépendant de la tension VBE en entrée. — Schéma équivalent possible de transistor bipolaire, faisant intervenir des éléments linéaires, dont un générateur de tension idéal dépendant de la tension V_BE en entrée.

Conclusion

Nous avons vu les composants de base passifs que sont la résistance, le condensateur et la bobine et les lois qui régissent courant et tension. Nous allons dans la suite les utiliser pour résoudre différents circuits.

Cet article vous a plu ? N’hésitez pas à le commenter ou à le partager, merci !!

1 Éléments passifs non réactifs