Que sont les dérivées et à quoi servent-elles?

Est-il nécessaire de savoir faire des dérivées ? Ou doit-on les garder comme un mauvais souvenir de lycée ? Tout dépend de ce que l’on veut faire. Lorsqu’on s’intéresse à un circuit, on peut utiliser un simulateur SPICE [1] et voir comment réagit le circuit en faisant varier les valeurs des composants.

Mais si on veut entrer un peu soit-il dans le détail, savoir d’où viennent les formules, il peut être intéressant de connaître quelques fondamentaux sur les dérivées.

Et vu que je parle assez souvent du sujet – des dérivées – dans ce blog, je me suis dit qu’il serait bien de lui consacrer un article.

Cependant, je n’ai pas la prétention d’entrer dans le pur formalisme mathématique. Je tente plutôt de donner une approche pratique qui, j’espère, vous donnera quelques clés pour comprendre davantage le langage mathématique.

Et, peut-être, vous faire goûter à la beauté des maths.

Sommaire

1 Un exemple : calcul de la vitesse

1.1 Vitesse constante

Imaginez que vous partiez de Paris en voiture pour aller à… Épinal (ma ville natale, mais peu importe). Pour faire rond, il y a 400 km, et il faut 4 heures pour faire le trajet.

La vitesse, par définition s’obtient en divisant la distance parcourue par le temps écoulé : v=d/t. Par conséquent v=400/4=100 km/h.

Pour aller de Paris à Épinal on roulerait donc à 100 km/h.

Mais vous savez bien que ceci n’est qu’une sorte de moyenne, car on ne roule pas à la même vitesse en ville que sur autoroute.

Par conséquent, la formule v=d/t n’est vraie que si la vitesse est constante.

1.2 Vitesse définie par segments

Si on sépare le trajet en différentes portions où la vitesse a été constante, on pourra utiliser la formule v=d/t sur chaque portion.

Imaginons qu’il y ait 4 portions de route :

Sortir de Paris : 30 km en 50 min
Autoroute : 305 km en 2 h 20
Route de campagne : 45 km en 30 min
Ville : 20 km en 20 min

Total : 400 km en 4 h (Note : j’ai cherché à utiliser des nombres ronds au détriments d’un certain réalisme…)

Calculons la vitesse sur chacune des portions

Sortir de Paris : v₁=30/50=0,6 km/min=36 km/h
Autoroute : v₂=305/140=2.17 km/min = 130 km/h
Route de campagne : v₃=45/30=1,33 km/min=90 km/h
Ville : v₄=20/20=1 km/min=60 km/h

(Note : pour ceux qui ont remarqué que j’ai dépassé la vitesse réglementaire sur certaines portions de route, nous allégueront que tout ceci se passait avant le 1er décembre 1990)

Je n’ai pu résister à la tentation de représenter ces chiffres su un graphe. Voici le tableau des données avec d la distance parcourue depuis Paris en km et t le temps écoulé depuis Paris en minutes.

	t1, d1	t2, d2	t3, d3	t4, d4	t5, d5
t(min)	0	50	190	220	240
d(km)	0	30	335	380	400

Et voici le graphe de la fonction d(t), on représente d en ordonnées et t en abscisses :

Les personnes qui ont lu cet article ont aussi lu : 3 questions sur l'exponentielle et le logarithme

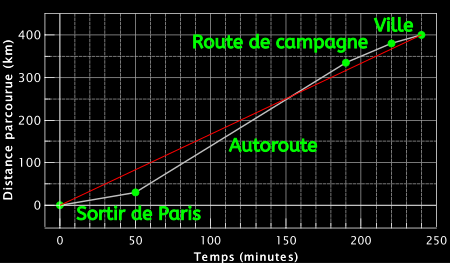
Graphe de la fonction distance parcourue - temps écoulé pour le trajet Paris-Épinal. Les données sont inventées pour illustrer le concept des dérivées.
La vitesse est donnée par la pente de chaque segment de droite. On voit donc bien graphiquement que c'est sur l'autoroute qu'on roule le plus vite. — Graphe de la fonction distance parcourue – temps écoulé pour le trajet Paris-Épinal. Les données sont inventées pour illustrer le concept des dérivées.
La vitesse est donnée par la pente de chaque segment de droite. On voit donc bien graphiquement que c’est sur l’autoroute qu’on roule le plus vite.

L’origine est en (0,0), c’est Paris. L’arrivée est en (240, 400), c’est Épinal. Le graphe obtenu est un graphe constitué de segments de droite. Comment trouve t’on la vitesse graphiquement ?

C’est la pente (ou coefficient directeur) de chacun des segments de droite. En effet, la vitesse est définie par v=d/t et d est placé en ordonnée et t en abscisse.

Et on le voit graphiquement : la pente du segment de droite Autoroute est la plus grande, c’est là où va le plus vite.

1.3 Détermination graphique de la vitesse

Imaginons maintenant le problème inverse, on nous donne le graphique précédent d(t) et on veut calculer la vitesse sur chacune des portions de route.

Recalculons donc graphiquement la vitesse, pour la portion autoroute. Nous devons calculer la pente de ce segment de droite. Pour cela prenons les deux points aux extrêmités :

$\displaystyle v_{autoroute}=\frac{d_2-d_1}{t_2-t_1}=\frac{335-30}{190-50}=\frac{305}{140}\simeq 2.17 km/min =130 km/h$

On retrouve bien 130 km/h à partir du graphique. On pourrait de même calculer la vitesse pour chaque segment de droite.

Ainsi, à la question « à quelle vitesse as tu roulé pour aller de Paris à Épinal ? », la réponse est « ça dépend, de où à où ? ».

1.4 Affinons le modèle

Imaginons maintenant que l’on sache la distance parcourue toutes les minutes : de la 1ère minute à la 2e. de la 2e a la 3e, de la 3e à la 4e, etc…

On nous fournit alors un graphe d(t) avec un segment de droite par minute. En faisant le rapport d/t pour chaque segment de droite on saurait donc la vitesse à laquelle on a roulé résolue à la minute près. On pourrait même tracer la vitesse en fonction du temps et lire que à la minute m on a roulé à la vitesse v.

Puis imaginons que l’on ait une précision sur la seconde, voire sur la milliseconde. Mieux, sur un temps infiniment petit ! On connaîtrait alors la vitesse en chaque point de la route et non sur une portion de route.

Et bien c’est cela le concept de dérivée ! C’est considérer qu’une fonction curviligne est composée de segments de droite juxtaposés et infiniment petits. En calculant leur coefficient directeur on obtient la fonction dérivée de la fonction étudiée.

En électronique, tension U , courant i et charge q peuvent être, selon les composants, reliés par la dérivée. Par exemple, dans un circuit contenant un condensateur il est « facile » de trouver q(t). Sachant que i est la dérivée de q par rapport à t, on en déduit facilement i(t).

2 Définition et notation de la dérivée

2.1 Du point de vue mathématique

Supposons une fonction f(x). Par fonction, nous entendons une quantité qui varie en fonction d’une variable x.

J’ai représenté une fonction f quelconque en rouge sur la figure suivante. On voit que c’est une fonction croissante, qui croît plus au début qu’à la fin et on voit surtout que ce n’est pas une droite.

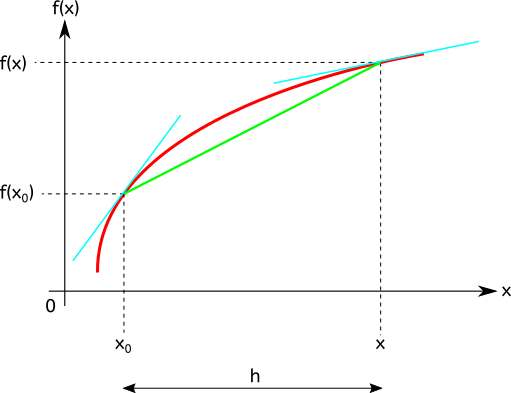
Courbe d'une fonction f(x) quelconque.
Les droites en bleu sont tangentes à la courbe. La dérivée de la fonction en un point c'est la pente de la tangente à la courbe en ce même point. — Courbe d’une fonction f(x) quelconque.
Les droites en bleu sont tangentes à la courbe. La dérivée de la fonction en un point c’est la pente de la tangente à la courbe en ce même point.

J’ai également représenté deux abscisses, x₀ et x, ainsi que leurs images par la fonction, f(x₀) et f(x).

On veut calculer le coefficient directeur k (ou pente) de la droite en vert. On utilise pour cela la définition du coefficient directeur, il est donné par le rapport entre l’écart en ordonnée f(x) – f(x₀) et l’écart en abscisse x – x₀ :

$\displaystyle k=\frac{f(x)-f(x_0)}{x-x_0}$

Très bien. Cependant dans le cas d’une courbe ce coefficient directeur ne nous sert pas à grand chose. Il est un peu équivalent à la vitesse moyenne calculée dans le paragraphe 1.1.

Et comme pour les vitesses sur les différentes portions de route, on voit qu’au début de la courbe, en x₀, la tangente à la courbe (représentée en bleu) est plus inclinée et en x elle l’est moins.

Les personnes qui ont lu cet article ont aussi lu : Notation scientifique et notation ingénieur

Comment peut on calculer le coefficient directeur de la droite bleue en x₀ ?

C’est très simple, on va rapprocher x de x₀. Plus x sera proche de x₀ , plus le coefficient directeur de la courbe verte sera proche de celui de la courbe bleue.

Pour définir la dérivée, on dit qu’on fait tendre x vers x₀ , cela s’appelle un calcul de limites en maths. On le note $\displaystyle \lim_{x\to x_0} machin$ , qui se lit limite quand x tend vers x₀ de machin. Et dans notre cas, machin est le coefficient directeur de la droite verte, soit k.

Voilà, on peut donc définir mathématiquement la dérivée de f en x₀. On la note soit f'(x), soit df/dx en x₀ :

$\displaystyle f'(x)=\frac{df}{dx}=\lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}$

Parfois, on utilisera la quantité h représentée sur la figure du dessus, avec h=x- x₀ .On trouve alors pour la définition de la dérivée :

$\displaystyle f'(x)=\frac{df}{dx}=\lim_{x\to x_0} \frac{f(x_0+h)-f(x_0)}{h}$

Ces définitions formelles servent à calculer la dérivée des fonctions usuelles x², 1/x, sin(x), exp(x), etc… Mais une fois qu’on connaît la forme des dérivées usuelles, on peut oublier la définition formelle de la dérivée.

Exemple de calcul de dérivée de fonction usuelle

Soit la fonction f(x)=x². Calculons sa dérivée grâce à la définition vue plus haut :

$\displaystyle f'(x)=\frac{df}{dx}=\lim_{x\to x_0} \frac{f(x_0+h)-f(x_0)}{h}$

On a que f(x)= x² donc f(x₀)= x₀ ² et f(x₀+h)= (x₀+h) ² = x₀² + 2x₀h + h²

Par conséquent :

$\displaystyle f'(x)_{|x=x_0}=\lim_{h\to 0} \frac{ (x_0+h)^2- x_0^2 }{h}= \lim_{ h\to 0 } \frac{ x_0^2 + 2x_0h + h^2 - x_0^2 }{h} = \lim_{ h\to 0 } \frac{ 2x_0h + h^2 }{h}= \lim_{ h\to 0 } \frac{ h(2x_0+ h) }{h}= \lim_{ h\to 0 } 2x_0 + h = 2 x_0$

car h tend vers 0, on peut l’annuler à la fin du calcul.

Nous venons de démontrer que la dérivée de x² par rapport à x est 2x.

Cliquez sur le bouton pour charger le contenu de docs.google.com.

Charger le contenu

2.2 Du point de vue de l’électronicien

L’électronicien doit connaître ce que sont basiquement les dérivées, et la forme de la dérivée de quelques fonctions usuelles.

Notations

En électronique, très souvent la variable sera le temps t, et non le x abstrait des maths. Et les fonctions sont les tensions, le courant, la quantité de charge, etc.

Par conséquent, les fonctions qui varient avec le temps se noteront U(t), i(t), q(t), etc. et la fonction dérivée sera par rapport à t. On notera donc dU/dt, di/dt, dq/dt,…

Fonctions usuelles et leurs dérivées

La définition de la dérivée nous permet de calculer les dérivées suivantes, en prenant U(t) pour l’exemple :

Fonction	Dérivée	Commentaires
U(t)= a	0	a est une constante, sa dérivée est nulle
U(t)=t	1	t est la variable
U(t)=at	a	On garde la constante multiplicative, que l’on multiplie par 1, la dérivée de t
U(t)=at+b	a
U(t)=sin(t)	cos(t)
U(t)=cos(t)	-sin(t)	Attention au signe –
U(t)= U₀ sin(t)	U₀ cos(t)	U₀ est une constante multiplicative, on la garde telle quelle.
U(t)=sin(at+b)	a cos(at+b)	L’intérieur du sinus est une fonction de t. On la dérive et on la multiplie par la dérivée de sin.
U(t)= U₀ sin(at+b)	a U₀ cos(at+b)
U(t)=exp(t)	exp(t)	Fonction exponentielle, sa dérivée est elle même
U(t)= U₀ exp(at+b)	a U₀ exp(at+b)	Pour les mêmes arguments que vus plus haut : on multiplie l’intérieur de la fonction exponentielle et on le multiplie par la dérivée de l’exponentielle qui est l’exponentielle elle même.

L’article suivant explique la fonction exponentielle.

3 Exemples pratiques de dérivées en électronique

Nous avons rencontré des dérivées à plusieurs reprises dans ce blog. Par exemple, dans l’article sur les résistances, condensateurs et bobine ou la résistance d’entrée et de sortie.

Maintenant que nous en savons plus, nous allons pouvoir les commenter.

3.1 Définition du courant

Le courant, en ampère (A) est défini comme la quantité de charges électriques qui passent à travers une section en un temps donné. C’est un peu comme le nombre de km par heure, mais ici c’est le nombre de charges par secondes.

Par conséquent, si vous avez bien lu le paragraphe nº1, vous comprendrez que le courant i est défini par le rapport entre la quantité de charge q et le temps passé t :

Les personnes qui ont lu cet article ont aussi lu : Les nombres complexes : bases

$\displaystyle i=\frac{q}{t}$

Maintenant, vous me direz que cela est vrai si le courant est constant avec le temps. S’il ne l’est pas, on doit utiliser la dérivée. Le courant est alors défini comme précédemment, mais avec des segments de droites infinitésimaux :

$\displaystyle i(t)=\frac{dq}{dt}$

Nous remarquons donc que si q(t)=constante, sa dérivée est nulle (voir le tableau précédant). Par conséquent i est nul.

Par conséquent il y a courant s’il y a variation de la quantité de charges dans le temps.

3.2 Déphasage induit par un condensateur

Supposons le circuit de la figure suivante :

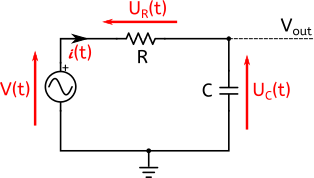
Circuit RC. Le condensateur entraîne un déphasage du courant sur la tension.

Ce circuit simple est composé d’une source de tension alternative, d’une résistance R et d’un condensateur de capacité C. La source délivre une tension sinusoïdale : la tension délivrée V est telle que V=V₀sin(ωt).

Le générateur va

d’une part provoquer une accumulation de charges q alternativement sur une armature du condensateur puis sur une autre, donnant lieu à une différence de potentiel aux bornes du condensateur U_C = q/C. On a donc q = C x U_C.
de surcroît imposer (au bout d’un certain temps dépendant de R et de C) son régime sinusoïdal. Par conséquent, U_C est de la forme U_C=U_C0sin(ωt). Ceci signifie que la tension aux bornes du condensateur est sinusoïdale, d’amplitude U_C0 et de même fréquence (ou pulsation) que V.

Connaissant U_c(t), calculons i(t)

Nous avons vu que le courant i est défini par une variation de charge dans le temps. On applique la formule de i vue dans le paragraphe précédant et on trouve que :

$\displaystyle i(t)=\frac{dq}{dt}=\frac{d(C\times U_c)}{dt} =C \frac{dU_c}{dt}$

Que s’est-il passé ? J’ai remplacé q par C x U_C dans la dérivée. Or, nous avons vu dans le tableau précédant que l’on peut sortir les constantes multiplicatives d’une dérivée. La capacité C est constante avec le temps, U_C ne l’est pas. Je peux donc sortir C de la dérivée.

Calculons la dérivée de U_C par rapport au temps :

$\displaystyle \frac{d U_c}{dt}=\frac{d(U_{C0}sin(\omega t))}{dt}=U_{C0}\frac{d (sin(\omega t))}{dt}= U_{C0} \times \omega \times cos (\omega t)$

où on a sorti U_C0 de la dérivée car l’amplitude est constante. Et pour le calcul de la dérivée du sinus on peut se référer au tableau vu plus haut où j’ai remplacé la constante a par ω.

Par conséquent, revenons à l’expression de i :

$\displaystyle i(t)=\frac{dq}{dt}=C \frac{dU_c}{dt} = C U_{C0} \omega cos (\omega t)$

On trouve que le courant a une amplitude CU_C0ω et qu’il est également sinusoïdal. Remplaçons finalement le cosinus par un sinus, sachant qu’ils sont déphasés de 90º c’est-à-dire π/2 en radians (cos(x)=sin(x+ π/2)). On trouve donc pour i :

$\displaystyle i(t)= C U_{C0} \omega sin (\omega t + \frac{\pi}{2})$

En notant i₀= CU_C0ω :

$\displaystyle i(t)= i_0 sin (\omega t + \frac{\pi}{2})$

Conclusion sur le déphasage entre U_C(t) et i(t)

Le calcul des dérivées nous montre que le condensateur conduit à :

un déphasage de 90º entre courant et tension
le courant est en avance sur la tension. Ceci signifie que le courant atteint son maximum avant la tension.

Voyons cela sur une figure :

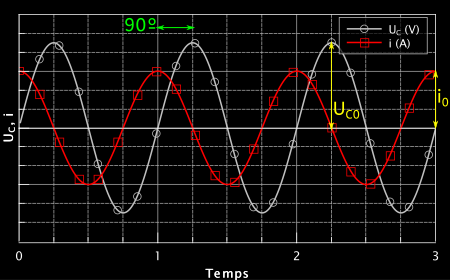
Représentation graphique de Uc(t) et i(t). Ils n'atteignent pas leur maximum en même temps. Le courant (en rouge) est en avance d'un quart de motif. Ce résultat s'explique par la présence d'une dérivée.
Les amplitudes sont représentées en jaune. — Représentation graphique de Uc(t) et i(t). Ils n’atteignent pas leur maximum en même temps. Le courant (en rouge) est en avance d’un quart de motif. Ce résultat s’explique par la présence d’une dérivée.
Les amplitudes sont représentées en jaune.

On peut faire la même chose avec la bobine et montrer le comportement inverse :

$\displaystyle U_L=L\frac{di}{dt}$

Par conséquent on peut montrer avec les dérivées qu’une bobine conduit à :

un déphasage de 90º entre courant et tension
le courant est en retard sur la tension. Ceci signifie que le courant atteint son maximum après la tension.

3.3 Un dernier mot sur le sens graphique des dérivées

Regardons la figure précédente, et souvenons nous que la dérivée n’est rien d’autre que le coefficient directeur de la tangente à la courbe en chaque point.

Vu que le courant est la dérivée de la tension, nous pouvons observer une cohérence entre la définition de la dérivée et sa représentation graphique :

Lorsque l’on gravite une montagne et que l’on est au sommet, que vaut la pente ? Zéro ! Lorsque l’on atteint le maximum on ne monte plus et on amorce la descente, la pente est donc nulle.

Regardons un maximum pour la tension : on voit que le courant s’annule ! La même chose se produit aux minimums de tension : sur tous les maximums et tous les minimums de U, le courant s’annule !

2. Lorsque la tension augmente, sa pente est positive donc le courant est positif.

3. Lorsque la tension diminue, sa pente est négative, donc le courant est négatif.

C’est beau non ??

Conclusion

Dans cet article j’ai fait une sorte de grande introduction aux dérivées, en tentant de montrer ce qu’elles sont et à quoi elle servent. J’ai abordé rapidement le comment, c’est-à-dire le côté technique du calcul pour ne pas surcharger . En tout cas j’espère que cet article vous aura donné envie d’en savoir plus sur les dérivées et de pratiquer le calcul dans des circuits types.

Avez vous aimé cet article ? Avez vous compris quelque chose ? N’hésitez pas à me le dire dans les commentaires !

Références

[1] https://fr.wikipedia.org/wiki/SPICE_(logiciel)

Cet article a 6 commentaires

GABER 11 décembre 2021 Répondre

Bonjour,
Merc pour cette présentation limpide et pédagogique
Bravo
1. fais-tes-effets-guitare.com 14 décembre 2021 Répondre
  
  Bonjour, merci pour votre commentaire ! 😊
  Si vous voulez que j’aborde d’autres thèmes sur les maths n’hésitez pas à me demander !
Bernard 15 novembre 2021 Répondre

Bonjour Olivier,

J’ai 65 ans et je viens découvrir ton site en faisant des recherches sur des cours de maths.
Je voulais te remercier pour ton approche non conventionnelle mais terriblement efficace de notions pas évidentes, surtout pour moi pour qui les cours de maths commencent à dater.
Alors merci et j’attends la suite avec impatience, il s’avère que j’ai été un peu gratteux en orchestre de variétés et comme l’électronique m’intéresse encore, je vais m’amuser avec certains de tes montages
Un grand bravo pour ce site original.

Un peu de pub pour le mien https://tabar57.blog4ever.com/

Bernard
1. fais-tes-effets-guitare.com 16 novembre 2021 Répondre
  
  Salut Bernard,
  merci beaucoup pour ton commentaire, ravi de pouvoir aider et content que tu trouves l’approche originale ! 🙂
  À bientôt !
Nathalie 15 mai 2021 Répondre

Bonjour
Je trouve votre site remarquable, vous avez une maniere d’expliquer les choses incroyablement simple et claire, je suis fan!
Juste une question, un point que je n’ai pas compris dans l’article sur les dérivées: pourquoi dit-on que le courant est la dérivée de la tension? Est-ce que ça vient de la lecture des 2 courbes à l’oscilloscope , ou est-ce qu’il y a une autre façon de l’expliquer?
Merci beaucoup!
1. fais-tes-effets-guitare.com 17 mai 2021 Répondre
  
  Bonjour Nathalie,
  
  tout d’abord merci tout plein pour votre commentaire sur le site ! 🙂
  
  Pour répondre à votre question, le courant est la dérivée de la tension, mais pas n’importe quelle tension, la tension aux bornes du condensateur. Par exemple ceci est faux pour la tension aux bornes d’une résistance car on a la loi d’Ohm, qui dit que courant et tension sont proportionnels, la constante de proportionnalité étant R.
  
  Maintenant pourquoi le courant est la dérivée de la tension aux bornes du condensateur ? C’est parce que le courant est défini par une variation de charge dans le temps. Si les charges ne bougent pas, il n’y a pas de courant. Je ne vais pas refaire l’explication de l’article qui explique que la dérivée est l’outil qui permet de traduire mathématiquement une variation. Mais donc cela signifie que le courant est donné par la dérivée de la charge (la quantité d’électrons) par rapport au temps. Et comme la tension aux bornes du condensateur est proportionnelle à la charge accumulée dedans (q = C x Uc), une variation de tension conduit à une variation de charge, donc une variation de courant. Par conséquent, le courant est défini par la dérivée de la tension. Plus exactement, i = dq/dt = C x d(Uc)/dt.