Micro de guitare électrique et perte d'aigus

Dans cet article nous allons voir comment en branchant la guitare à l’ampli, nous créons inéluctablement un filtre passe-bas qui filtre nos aigus.

L’article précédent traitait de l’effet des résistances d’entrée/sortie sur l’amplitude du signal transmis, nous avons vu que pour que toute la tension de la source se retrouve sur la charge, il faut que la résistance de la charge soit très grande devant celle de la source.

Dans cet article nous avions également introduit le terme d’impédance, qui nous permet de regarder comment varie l’amplitude du signal avec la fréquence.

Ici, nous définirons un peu mieux ce qu’est l’impédance. Nous pourrons alors affiner le modèle du micro de guitare en introduisant une bobine, et voir son effet sur la tonalité du son, dans le cas d’une guitare passive.

Les 2 premières parties se lisent facilement, il n’y a pas de maths. En revanche, dans la 3e partie j’ai introduit la démonstration mathématique de ce qui est dit. Ce sont des maths un peu poussés, mais nécessaires pour aller en profondeur dans les problèmes en électronique. Mais rassurez vous, je compte écrire quelques articles dédiés aux mathématiques appliquées bientôt (dérivées et nombre complexes prochainement).

Sommaire

1 Rappels sur le concept d’impédance

L’impédance se note Z. Comme la résistance, elle traduit l’opposition au passage du courant. Cependant, pour certains composants elle varie avec la fréquence et elle introduit un déphasage du signal (fréquence et phase sont définis dans cet article).

L’impédance est définie en régime alternatif sinusoïdal. Voyons un peu plus en détail sa dépendance en fréquence.

1.1 Résistance

La valeur de résistance d’une résistance ne varie pas avec la fréquence du signal qui le parcourt.

Ceci veut dire qu’une résistance de 10 kohms vaudra toujours 10 kohms que le signal ait une fréquence de 10 Hz ou de 10 kHz.

1.2 Condensateur

Condensateurs et bobines vont s’opposer au passage du signal alternatif d’une manière qui va dépendre de la fréquence de celui-ci.

En effet, je vous ai déjà parlé de cela pour le condensateur (voir l’article comment sonne un condensateur). Nous avons vu que, étant composé d’un isolant, il ne laisse pas passer le courant continu. Il transmet le courant alternatif car celui-ci provoque un mouvement d’électron. Cette onde électronique se transmet d’une armature du condensateur à l’autre , d’une quantité qui va dépendre de la fréquence f du signal, de la valeur C de la capacité et de la valeur R de la résistance qu’on doit introduire dans le circuit.

Les personnes qui ont lu cet article ont aussi lu : Résistance d'entrée/sortie et effet sur l'amplitude du signal transmis

Nous avons alors vu qu’un condensateur est équivalent à :

un interrupteur ouvert à basse fréquence
un interrupteur fermé à haute fréquence

1.3 Bobine

Une bobine de cuivre a un caractère inductif.

Ceci signifie que le mouvement des électrons provoqué par le signal alternatif va induire (créer) un champ magnétique dans la bobine. Et ce champ électrique va créer une force électromotrice qui va s’opposer au mouvement des électrons [1].

Plus la fréquence du signal est grande, plus la force électromotrice induite est grande et s’opposera au passage du courant. L’impédance de la bobine est donc grande à haute fréquence et petite à basse fréquence.

Comme nous l’avons fait avec le condensateur, la bobine peut se modéliser par :

un interrupteur fermé à basse fréquence
un interrupteur ouvert à haute fréquence

Nous remarquons finalement que le modèle de la bobine est qualitativement inverse à celui du condensateur.

2 Le micro guitare : 2e approche

Nous allons ici nous intéresser au micro d’une guitare électrique. Celui-ci est composé d’une bobine de fil de cuivre (ou parfois deux !).

Modèle du micro de guitare électrique

Nous pouvons donc affiner le modèle du micro guitare vu en 1ère approche dans l’article précédant Nous le modèliserons comme un générateur de tension sinusoïdal en série avec une bobine et une résistance interne.

Voici à gauche le circuit d’un micro guitare connecté à la résistance d’entrée R_IN d’un ampli :

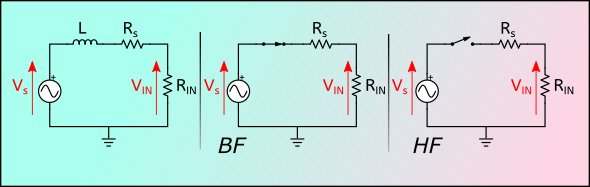
À gauche : circuit de la guitare connectée à l'entrée de l'ampli. Au milieu et à droite, simplification à basse fréquence (BF) et à haute fréquence (HF). — À gauche : circuit de la guitare connectée à l’entrée de l’ampli. Au milieu et à droite, simplification à basse fréquence (BF) et à haute fréquence (HF).

Au milieu, j’ai représenté le circuit à basse fréquence (BF). La bobine est alors équivalente à un fil. Et si on rempli la condition R_IN >> R_s on est dans le cas idéal et alors V_IN = V_s (vous ai-je dis de relire l’article précédent ?).

À droite, c’est le cas d’un signal haute fréquence (HF). La bobine est équivalente à une interrupteur ouvert. Aucun courant ne circule dans le circuit, et donc V_IN=0.

Notion de fréquence de coupure

Nous voyons donc un effet très intéressant : lorsque vous branchez votre guitare à l’ampli vous créez d’emblée un filtre passe bas – un filtre qui va virer tous vos aigus – et ceci avant même d’entrer dans la section préampli et équalisation de l’ampli.

Voici la figure type d’un filtre passe-bas, montrant l’amplitude du son (le gain) en fonction de la fréquence du signal :

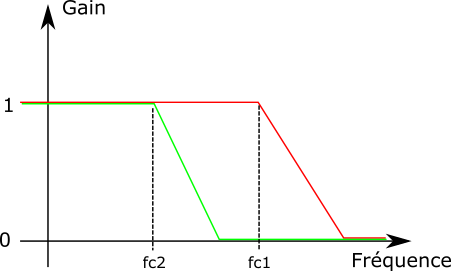
Gain du circuit en fontion de la fréquence d'un circuit passe bas. Les hautes fréquences sont filtrées à partir de la fréquence fc. Les basse fréquence sont transmises sans atténuation. — Gain du circuit en fontion de la fréquence d’un circuit passe bas. Les hautes fréquences sont filtrées à partir de la fréquence fc. Les basse fréquence sont transmises sans atténuation. Le filtre vert coupe davantage d’aigus que le filtre rouge.

f_c signifie fréquence de coupure. À gauche, le gain vaut 1 donc tout le signal passe. À droite le signal transmis décroît, jusqu’à devenir négligeable. J’ai mis deux exemples de fréquence de coupure, que j’ai appelé f_c1 et f_c2.

Les personnes qui ont lu cet article ont aussi lu : Calcul de résistance équivalente

Par le calcul on peut montrer que f_c diminue lorsque la résistance d’entrée de l’ampli (ou de la 1ère pédale) R_IN diminue. Par conséquent si R_IN est insuffisamment grand, la fréquence de coupure est trop petite et la diminution d’aigus de notre son non négligeable.

Ceci explique pourquoi il faut que notre amplificateur de guitare ait une impédance d’entrée élevée de 1 Mohm. D’une part pour que la chute de potentiel aux bornes de la résistance de sortie soit négligeable. D’autre part pour ne pas être gêné par le filtre passe-bas.

La formule qui donne la fréquence de coupure f_c en fonction de la résistance d’entrée R_IN et l’inductance du micro L est la suivante :

$\displaystyle f_c=\frac{R_{IN}}{2\pi L}$

D’ailleurs, nous allons la démontrer dans un instant, mais auparavant, faisons une petite application numérique.

Application numérique

L’inductance d’un micro guitare est compris entre 1 et 15 H [2]. Supposons un micro single coil d’inductance L=2 H et une résistance d’entrée de 1 Mohms. Prenons également en compte le potentiomètre de volume de la guitare, typiquement 500 kohms. La résistance de charge équivalente est constituée de ces deux résistances en parallèle, on trouve une résistance équivalente de 333 kohms. Calculons la fréquence de coupure :

$\displaystyle f_c=\frac{333^3}{2\pi \times 2} \simeq$ 26 kHz

Ceci est raisonnable, au dessus de la limite du spectre audible.

Prenons maintenant un micro humbucker, dont l’inductance est plus grande, prenons 10 H.

$\displaystyle f_c=\frac{333^3}{2\pi \times 10} \simeq$ 5 kHz

On trouve une bonne différence tonale.

Imaginez maintenant que l’on branche la guitare a un ampli de résistance d’entrée bien plus faible, ou à une vieille pédale d’effet dont la valeur de résistance d’entrée est faible car ce n’était peut-être pas la préoccupation première de l’époque… vous commencez à comprendre si ce n’était pas le cas que le set entier a une influence sur la tonalité !!

3 Maths : filtre LR

Ce paragraphe est un peu technique. Il n’est pas nécessaire à la compréhension de cet article, il sert juste de démonstration pour calculer la fréquence de coupure dans le cas d’un filtre LR et retrouver le résultat donné plus haut.

Il fait appel au fait que l’impédance est un nombre complexe. Et oui, ce n’est pas un nombre réel. La valeur de l’impédance renseigne sur la valeur de la résistance du composant mais aussi sur le déphasage du signal audio auquel elle conduit.

L’impédance complexe est définie à partir d’une onde sinusoïdale. Dans le cas d’une bobine, on trouve que l’impédance Z_L vaut :

$Z_L=j\omega L$

avec j le nombre complexe tel que j²=-1 et ω la pulsation. La pulsation et la fréquence sont liées par la formule ω=2πf_c.

Résolution en utilisant l’impédance équivalente

Le circuit micro guitare + entrée ampli est représenté à gauche :

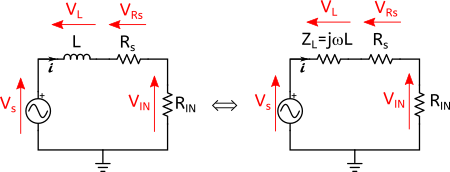
À gauche : circuit du micro guitare connecté à l'entrée de l'ampli. À droite : résolution par la méthode des impédances équivalentes. — Circuit du micro guitare connecté à l’entrée de l’ampli (à gauche). Résolution par la méthode des impédances équivalentes (à droite).

À droite j’ai remplacé la bobine par une résistance d’impédance jωL. Pour obtenir le gain de ce circuit en fonction de la fréquence, on cherche d’abord à définir la fonction de transfert H(jω) du circuit. H(jω) est définie par :

Les personnes qui ont lu cet article ont aussi lu : Quizzz #1 : unités et éléments passifs

$\displaystyle H(j\omega)=\frac{V_{IN}}{V_s}$

et le gain G en fonction de la fréquence est défini par le module de H(jω) :

$\displaystyle G(\omega)=\left| H(j\omega) \right|$

Calcul de la fonction de transfert H (jω)

Calculons H(jω) : d’une part on applique la loi d’Ohm en V_IN pour trouver une expression de i :

$\displaystyle V_{IN}=i \times R_{IN}$ . Donc $\displaystyle i=\frac{V_{IN}}{R_{IN}}$ .

D’autre part on applique la loi des mailles dans le circuit et la loi d’Ohm :

$\displaystyle V_s=V_{IN}+V_{Rs}+V_L=i \times (R_{IN}+R_s+j\omega L)$

En injectant l’expression de i trouvée auparavant dans cette équation on trouve :

$\displaystyle V_s=\frac{V_{IN}}{R_{IN}}\left(R_{IN}+R_s+j\omega L\right)$

Et cette équation nous permet de trouver H(jω) que l’on a défini plus haut :

$\displaystyle H(j\omega)=\frac{V_{IN}}{V_s}=\frac{R_{IN}}{R_{IN}+R_s+ j\omega L }$

En divisant en haut et en bas par R_IN et en supposant que la résistance d’entrée R_IN est très grande devant R_s cette équation devient :

$\displaystyle H(j\omega) =\frac{1}{1+ j\omega \frac{L}{ R_{IN} } }$

En posant $\displaystyle \omega_c=\frac{R_{IN}}{L}$ on obtient l’équation généralisée d’un filtre LR :

$\displaystyle H(j\omega) =\frac{1}{1+ j\frac{ \omega }{ \omega_c } }$

Déduisons la formule du gain et la fréquence de coupure

Par conséquent on trouve pour le gain G :

$\displaystyle G(\omega)=\left| H(j\omega) \right|= \frac{1}{\sqrt{1+ \left(\frac{ \omega }{ \omega_c }\right)^2} }$

Soit en exprimant G en fonction de la fréquence :

$\boxed{\displaystyle G(f)= \frac{1}{\sqrt{1+ \left(\frac{ f }{ f_c }\right)^2} } }$

On retrouve donc bien l’expression de la fréquence de coupure vu plus haut :

$\boxed{\displaystyle f_c=\frac{R_{IN}}{2\pi L}}$

Représentation graphique du gain

Voyons ce qui se passe pour différentes valeurs de fréquence en regardant l’expression de G(f):

pour f<<f_c, f/f_c ~ 0 et donc G=1
pour f>>f_c : G tend vers 0
f=f_c : G=1/ √ 2~0.707

J’ai tracé sur la figure suivante l’allure du gain en fonction de la fréquence avec l’équation G(f) établie plus haut :

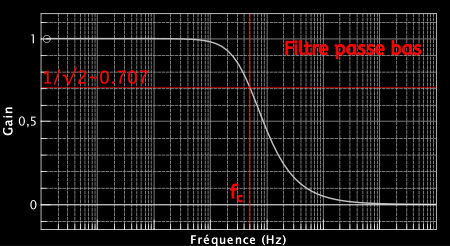
Le gain du filtre LR vu ici passe de l'unité à 0. Au delà d'une certaine fréquence fc le gain chute. On a donc un filtre passe-bas. — Le gain du filtre LR vu ici passe de l’unité à 0. Au delà d’une certaine fréquence fc le gain chute. On a donc un filtre passe-bas.

4 Résumé et perspectives

Dans cet article nous avons modélisé le micro d’une guitare électrique par une générateur de tension sinusoïdal, une bobine et une résistance interne.

Les conséquences sont les suivantes :

En branchant la guitare à l’ampli on forme un circuit passe-bas qui coupe les aigus de notre son
La fréquence de coupure dépend de l’inductance de la bobine et de la résistance d’entrée de l’ampli
Si la résistance d’entrée de l’ampli est trop basse, la fréquence de coupure diminue et plus d’aigus sont filtrés.

Et nous comprenons qu’en branchant une guitare passive sur une table de mixage, la faible résistance d’entrée de celle-ci va nous faire perdre du gain mais aussi des aigus. On peut résoudre cela en utilisant une DI, mais à mon goût ceci est bien mais pas top.

Dans le prochain article de cette série nous irons encore plus loin en matière de « tone sucking » : qu’est-ce ? Comment y remédier ?? Qu’est-ce qu’un « buffer » ???

Vous avez aimé cet article ? n’hésitez pas à le commenter, merci !!

Références

[1] https://fr.wikipedia.org/wiki/R%C3%A9actance_(%C3%A9lectricit%C3%A9)
[2] Denton J. Dailey, Electronics for Guitarists, ed. Springer