Le pont diviseur de tension

Dans cet article nous allons voir ce qui se cache derrière le concept de pont diviseur de tension.

Nous avons déjà rencontré le pont diviseur de tension dans ce blog, par exemple dans l’article sur l’alimentation d’un amplificateur opérationnel en alimentation simple. Les résistances du pont sont alors choisies afin de réduire la tension d’alimentation de 9 V à 4,5 V.

Nous l’avons également rencontré pour comprendre le fonctionnement des filtres (voir filtre RC et RAT).

Ce circuit est composé d’au moins 2 résistances en série, l’objectif étant de réduire une tension donnée à une tension voulue :

Voyons plus en détails quelle est l’influence des résistances R_A et R_B de la figure ci-dessus sur la tension de sortie U_A.

1 Un exemple

Regardons le pont diviseur de tension dans un cas concret :

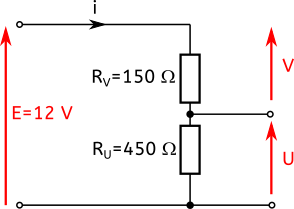
Ce circuit est constitué de 2 résistances en série de 150 et 450 ohms. Aux bornes de ce circuit on applique une tension constante de 12 V qui est celle qu’on dispose (donnée par notre générateur par exemple).

Ce circuit permet de faire chuter la tension aux bornes de R_V et donc d’obtenir une tension plus petite que 12 V en R_U.

Imaginons que nous ayons besoin d’une tension de 8 V. Voyons si ce circuit permet d’obtenir cette tension.

Calcul du courant dans le circuit

Pour cela on va calculer le courant qui passe dans le circuit. Nous savons que la résistance équivalente à 2 résistances en série est donnée par la somme des 2 résistances.

Par conséquent la résistance équivalente R du circuit vaut 150 + 450 = 600 ohms.

La loi d’Ohm nous dit qu’aux bornes d’une résistance la tension et le courant sont proportionnels : E=R×i. Nous connaissons E, et nous venons de calculer R. Nous pouvons donc déduire i :

i=E/R=12/600=0.02 A=20 mA.

Rappelons que le courant se mesure en ampères dont le symbole est A. Pour désigner un courant plus petit, on utilise le milliampère de symbole mA (vous pouvez consulter l’article sur les unités pour plus de détails).

Parfait, nous avons donc calculé que dans notre circuit, en appliquant une tension de 12 V, on a un courant de 20 mA qui circule.

Calcul de la tension U

La question maintenant est : quelle est la tension U aux bornes de la résistance R_U ?

C’est très simple ! On va encore utiliser la loi d’Ohm, non sur tout le circuit mais juste sur la résistance R_U.

Nous avons donc que U=R_U×i. On cherche U, on laisse donc la formule comme ça et on trouve :

U = 450 × 0,02 = 9 V.

On trouve qu’avec les résistances du circuit tel que présenté, on n’a pas 8 V comme on le voulait, mais 9 V.

Cependant, on comprends bien qu’en changeant les valeurs des résistances, on va pouvoir obtenir 8 V ou n’importe quelle tension comprise entre 0 V et 12 V.

Voyons comment faire cela dans un cas général.

2 Le pont diviseur de tension

Penchons nous sur le cas général pour déterminer les résistances du pont diviseur de tension. Partons donc de la figure suivante :

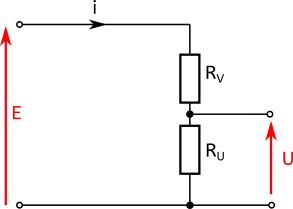
L’idée est toujours la même : nous voulons faire chuter l’excès de tension sur la résistance R_V afin d’obtenir la tension désirée aux bornes de R_U.

Nous allons reprendre les étapes du calcul de l’exemple précédant.

Calculons le courant $i$ qui circule dans le circuit en appliquant la loi d’Ohm. La résistance totale vaut $R_U + R_V$ et la tension appliquée vaut $E$.

Par conséquent, $E=(R_U+R_V)\times i$.

Nous déduisons $i$ :

$i=\frac{E}{R_U+R_V}$.

Voilà, nous avons une expression pour $i$. Nous la gardons de côté car nous allons l’utiliser dans un instant.

Calculons maintenant la tension $U$ aux bornes de $R_U$, toujours avec notre amie la loi d’Ohm : $U=R_U \times i$.

Injectons dans cette expression la formule que nous avons trouvé pour $i$ :

$U=R_U \times i = R_U \times \frac{E}{R_U+R_V}$

Que l’on peut réécrire :

$$U=E \times \frac{R_U}{R_U+R_V}$$

Ça y est, on a l’expression du pont diviseur de tension !!

Que signifie cette expression ? Que $U$ est une fraction de $E$. En effet, on voit que $U$ c’est $E$ multiplié par $\frac{R_U}{R_U+R_V}$ qui est compris entre 0 et 1.

Si $R_V=0$, on n’a pas de pont diviseur de tension et $U=E$. Si on augmente la valeur de $R_V$, le dénominateur devient plus grand que le numérateur et $U<E$.

Notons également que cette formule fait apparaître la tension désirée $U$, la tension donnée $E$ et les 2 résistances du pont diviseur de tension $R_U$ et $R_V$.

3 Retour sur l’exemple du début

Nous voulions une tension de 8 V aux bornes de R_U, mais nous avions trouvé 9 V avec les résistances proposées. Supposons que R_U soit imposée et que l’on ait le choix sur R_V. Calculons la résistance R_V à placer pour obtenir U=8 V.

Rappelons l’expression du pont diviseur de tension :

$U=E \times \frac{R_U}{R_U+R_V}$

Alors soit on connaît ses maths et on trouve l’expression de R_V, soit on fait varier R_V dans un tableur et on regarde pour quelle valeur de R_V on a U=8V.

Déterminons R_V par dichotomie

Voici par exemple un tableau calculé dans Excel :

RV (ohms)	100	150	200	250	300	350	400	450
U (V)	9.81	9	8.31	7.71	7.2	6.75	6.35	6

Ce tableau montre que pour obtenir U=8 V il faut que R_V soit compris entre 200 et 250 ohms. Ensuite on peut affiner pour trouver une valeur plus précise de R_V.

C’est une manière tout à fait valide de trouver R_V qui évite de se prendre la tête avec les équations. Cependant, je préfère trouver mathématiquement l’expression de R_V car ensuite le calcul est immédiat.

Déterminons R_V par le calcul

On cherche à isoler $R_V$ de l’expression précédente pour trouver une expression du type $R_V=…$

Partons de l’expression du pont diviseur de tension :

$U=E \times \frac{R_U}{R_U+R_V}$

Je fais passer $(R_U+R_V)$ à gauche :

$U \times (R_U+R_V)=E \times R_U$

Je développe à gauche :

$U \times R_U+ U \times R_V=E \times R_U$

Je fais passer $U \times R_U$ à droite pour ne garder que les termes qui contiennent $R_V$ à gauche :

$U \times R_V=E \times R_U -U \times R_U$

Puis on isole $R_V$ en passant le $U$ de gauche à droite, c’est-à-dire en divisant tout par $U$ :

$R_V=\frac{E}{U }\times R_U -R_U$

Que l’on peut réécrire plus joliment en factorisant par $R_U$ à droite :

$R_V=R_U\left(\frac{E}{U }-1 \right)$

Remplaçons alors $E=12 V$, $U=8 V$ et $R_U=450 \Omega$ :

$R_V=450 \left(\frac{12}{8 }-1 \right)=225 \Omega$.

Voilà, nous venons de calculer qu’il faut une résistance R_V de 225 ohms pour avoir 8 V aux bornes de R_U.

À votre tour, si on veut U=6 V, quelle valeur doit-on choisir pour R_V ? Mettez votre résultat dans les commentaires !

4 Limites du pont diviseur de tension

Pour terminer cet article, je dois tout de même mentionner que le pont diviseur de tension n’est pas efficace pour alimenter des circuits à charge variable. Regardez la figure suivante :

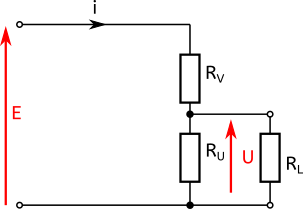
J’ai branché le circuit sur une résistance de charge R_L. Le fait d’ajouter une résistance en parallèle diminue la valeur de la résistance équivalente du circuit. Par conséquent le courant augmente, ce qui augmente la chute de tension en R_V et diminue la tension en R_U.

Si R_L est très grande devant R_U, peu de courant est dévié vers elle. Par conséquent il n’y a pas de grosse influence de R_L sur le circuit et l’expression du pont diviseur de tension reste valable.

Maintenant si R_L est trop petite, la résistance équivalente à R_U et R_L diminue ce qui diminue significativement la tension aux bornes de R_U.

De plus, si R_L varie, U variera aussi ce qui rend ce montage inefficace pour ce qui est de stabiliser la tension.

Pour éviter cet inconvénient, on a recours à d’autres types de montages (à base de diode Zener par exemple) qui permettent d’obtenir une tension constante même quand le courant absorbé par la charge varie. Mais ce sera l’objet d’un nouvel article !

Vous avez des questions ? N’hésitez pas à les laisser en commentaire !