Filtre RC et RAT

Nous parlons de manière récurrente de filtres dans ce blog. En effet, ils sont présent dans toute une variété de pédales d’effet, car ils permettent de sculpter le son, voir par exemple la Moogerfooger MF-101 ou la Pralines de Glou-Glou. En studio, ils permettent de faire coexister différents instruments ou d’atténuer les fréquences non désirées. Un autre exemple de pédale d’effet sont les pédales wha-wha qui sont composées d’un filtre dont on change les caractéristiques avec le pied.

Mais qu’est-ce qu’un filtre ?

C’est un circuit qui permet de choisir quelles fréquences vont passer et quelles fréquences sont bloquées. Mais pourquoi parle t’on de fréquences, pourquoi y en a t’il plusieurs ?

Pour comprendre cela, nous avons abordé le thème des spectres dans un article précédant. Nous y avons vu que le signal audio peut être décrit comme une somme infinie de sinusoïdes. À l’aide d’un filtre, nous allons choisir quelle(s) partie(s) du spectre nous allons laisser passer voire amplifier, et quelle(s) partie(s) nous voulons atténuer. Avec les filtres on va donc pouvoir jouer sur le spectre du son et exalter notre exploration sonore !

Dans cet article, nous allons mettre en équation le comportement d’un filtre. Pour cela nous allons considérer un cas simple, un circuit RC passif. C’est d’ailleurs le circuit que l’on trouve dans la RAT. Auparavant nous allons voir quelques exemples de filtres pour se faire une idée pratique de ce qu’ils font.

1 Quelques exemples de filtres dans les pédales

Commençons par voir quelques exemples de filtres dans des circuits.

1.1 Proco RAT : Filtre RC

Voici la partie filtre de la RAT (la pédale de distorsion archi-connue) :

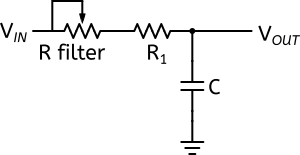
On voit que ce filtre est très simple, il ne contient que 3 composants : une résistance variable en série avec une résistance et un condensateur. Notons que ce dernier est relié à la masse.

Voici une manière très rapide de comprendre ce qui se passe : nous savons qu’un condensateur se comporte comme un interrupteur ouvert pour les basses fréquences et un interrupteur fermé pour les hautes fréquences.

Par conséquent, les basses fréquences voient une grande résistance tandis que les hautes fréquences voient un fil et sont court-circuitées.

Il en suit que les basse fréquence continuent le chemin audio comme si de rien était, tandis que les hautes fréquences sont envoyées vers la masse (chemin de moindre résistance oblige). À « l’arrivée », on ne trouve donc que les basses fréquences. On appelle donc ce filtre un filtre passe-bas et voici son allure :

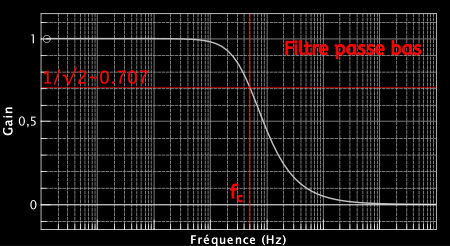
La fréquence de coupure $f_c$ est la fréquence à partir de laquelle on considère que le filtre « agit ». Dans le cas du filtre de la RAT, elle est contrôlable par le musicien par l’intermédiaire du potentiomètre. Nous allons y revenir.

1.2 Gargletron : Filtre MFB

Et voici un autre exemple de filtre, bien plus compliqué quant au nombre de composants et aux maths qu’il y a derrière :

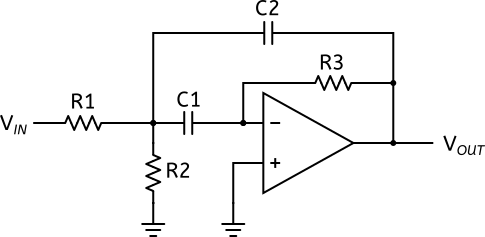
Ce filtre s’appelle un filtre MFB, pour Multiple FeedBack. Nous avons rencontré ce type de filtre dans l’article Ré-création DIY #1 : Gargletron.

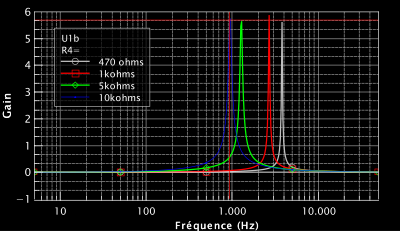
Ce filtre est dit « actif », car l’amplificateur opérationnel qui le compose nécessite d’être alimenté. En sortie, il ne laisse passer qu’une fenêtre en fréquence, c’est donc un filtre passe-bande. Et vous vous en doutiez, on définit les caractéristiques du filtre par les valeurs de R1, R2, R3, C1 et C2.

Voici l’allure de ce filtre :

2 Le filtre RC : maths

Nous allons étudier le filtre de la RAT en équations. Pour cela, nous allons utiliser le formalisme des nombres complexes.

2.1 Passons aux impédance complexe

Pour cela, la 1ère étape est de convertir tous les éléments passifs en leur équivalent complexe. Rappelons que :

• une résistance reste une résistance
• l’impédance complexe d’un condensateur est $\Large \frac{1}{j\omega C}$
• l’impédance complexe d’une bobine est $j\omega L$

Nous obtenons donc le circuit équivalent suivant :

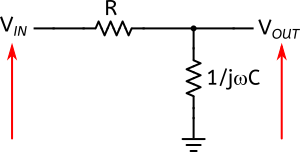
Nous avons remplacé le condensateur par une impédance complexe de valeur $\Large \frac{1}{j\omega C}$ et pour la résistance, nous avons juste sommé les deux résistances en série : $R=R_{filter}+R_1$. L’impédance du condensateur dépend de la fréquence, celle de la résistance est fixe.

Ce qu’on cherche, c’est la tension de sortie $V_{OUT}$. Celle-ci aura une valeur soit égale à la tension d’entrée $V_{IN}$, soit inférieure, car tous les éléments qui composent ce filtre sont passifs. Nous verrons en particulier que $V_{OUT}$ dépend de la fréquence du signal.

Notons qu’il existe également des filtres actifs, qui en plus d’atténuer amplifient aussi le signal aux fréquences souhaitées et requierent donc un apport d’énergie en échange.

2.2 1ère expression de $V_{OUT}$

Calculons l’expression de $V_{OUT}$ en fonction de $V_{IN}$ et des impédances présentes dans le circuit. Pour cela on remarque que ce circuit n’est rien d’autre qu’un pont diviseur de tension. Je rappelle son expression :

Cette formule nous donne la tension $U_A$ en $R_A$ en fonction de la tension totale $E$ et de $R_B$. On voit par cette formule que $U_A$ est plus petit que $E$ car on multiplie $E$ par $\Large \frac{R_A}{R_A+R_B}$ qui est plus petit que 1. En effet, on a nécessairement $R_A<R_A+R_B$.

Nous allons appliquer cette formule dans le cas du filtre de la RAT. Pour cela, on remarque que $E$ c’est $V_{IN}$, $R_B$ c’est $R$, $R_A$ c’est $\Large \frac{1}{j\omega C}$ et $U_A$ c’est $V_{OUT}$. Par conséquent :

$V_{OUT}=V_{IN}\times \Large \frac{\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}}$

où nous avons gentiment remplacé les résistances qui sont des nombres réels par les impédances qui sont des nombres complexes. Il va donc falloir faire le calcul dans l’ensemble des nombres complexes. J’ai écrit un article qui donne quelques bases, suffisantes pour comprendre cet article. Vous pouvez les lire ici.

2.3 Module de $V_{OUT}$

$V_{IN}$ est un signal alternatif périodique puisque c’est un son. Son amplitude étant fixe, c’est la quantité $\Large \frac{\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}}$ de l’expression précedante qui va nous donner l’évolution de $V_{OUT}$ avec la fréquence. Cette quantité va réduire l’amplitude d’entrée c’est à dire l’atténuer et induire un déphasage.

Réécrivons « mieux » cette quantité en multipliant en haut et en bas par la quantité $j\omega C$ :

$
\Large \frac{\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}} = \frac{1}{1+j\omega R C}
$

Pour calculer l’atténuation on calcule le module de $\Large \frac{R}{R+\frac{1}{j\omega C}}$. En mathématiques, le module se note entre deux barres verticales :

$
\begin{array}{|c|cc}
\Large \frac{\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}} & = & \Large \frac{1}{\sqrt{1+(\omega R C)^2}}
\end{array}
$

Nous allons appeler $\omega_c$ la quantité $\Large \frac{1}{RC}$. L’expression précédante devient :

$
\begin{array}{|c|cc}
\Large\frac{\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}} &=& \Large \frac{1}{\sqrt{1+\left(\frac{\omega}{\omega_c}\right)^2}}
\end{array}
$

$\omega_c$ s’appelle la pulsation de coupure du filtre. On lui associe $f_c$ que l’on appelle la fréquence de coupure. $f_c$ est égal à $\Large\frac{\omega_c}{2\pi}$ et correspond à la fréquence à laquelle on considère que le filtre « agit », c’est à dire ne laisse plus passer le signal.

Nous pourrions également calculer le déphasage, mais nous le ferons dans une étude plus poussée sur les filtres.

Par conséquent, nous trouvons en remplaçant la pulsation par la fréquence que :

$$V_{OUT}=V_{IN}\times \frac{1}{\sqrt{1+\left(\frac{f}{f_c}\right)^2}}$$

2.4 Évolution de $V_{OUT}$ avec la fréquence

Afin de se faire une idée plus précise de ce que signifie cette expression, nous allons tracer $V_{OUT}$ en fonction de la fréquence $f$. Auparavant, regardons le comportement de $V_{OUT}$ aux valeurs extrêmes de $f$ :

• lorsque $f$ est très petit devant $f_c$, $\frac{f}{f_c}\simeq 0$ par conséquent $V_{OUT} \simeq V_{IN}$ : les basses fréquences passent.
• lorsque $f$ est très grand devant $f_c$, $\frac{f}{f_c}$ est très grand. Par conséquent, $1+\left(\frac{f}{f_c}\right)^2$ est très grand et $\frac{1}{\sqrt{1+\left(\frac{f}{f_c}\right)^2}}$ tend vers 0, c’est-à-dire est très petit. Donc $V_{OUT} \simeq 0$ : les hautes fréquences ne passent pas.
• enfin, lorsque $f=f_c$, on trouve que $V_{OUT} = \frac{V_{IN}}{\sqrt{2}}$. Ce nombre prends une signification lorsque l’on parle de gain en décibels, ce dont on ne parlera pas ici.

Voici l’allure du graph :

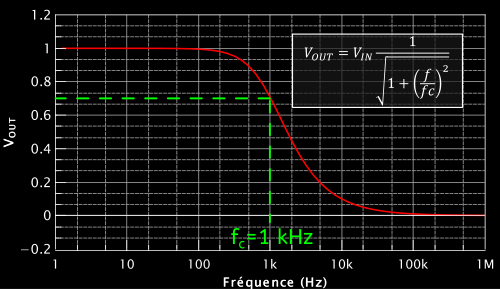
Sur ce graph j’ai choisi arbitrairement une fréquence de coupure de 1kHz. L’axe des abscisses est en échelle logarithmique, qui permet de voir l’évolution sur une grande plage de fréquences (ici de 1 Hz à 1 MHz).

En pratique, pour avoir 1 kHz, on choisit R et C de manière à ce que $\frac{1}{2\pi RC}$=1000. Par exemple si C=100nF, on choisira R~1,5kohms.

2.4 Revenons au cas de la RAT

Si on veut faire bouger la fréquence de coupure, on utilisera pour $R$ un potentiomètre monté en résistance variable, comme dans le cas de la RAT.

On peut s’amuser à calculer les fréquences de coupures extrêmes, c’est à dire lorsque la résistance du potentiomètre vaut 0 ohm, et lorsqu’elle vaut 100 kohms.

Rappelons que nous avons aussi une résistance fixe que j’ai appelé $R_1$ sur la figure vue plus haut, $R_1$=1,5 kohms. De plus, $C$=3,3 nF.

Et de ce que nous avons vu plus haut, la formule de $f_c$ est :

$$ f_c=\frac{1}{2\pi R C}$$

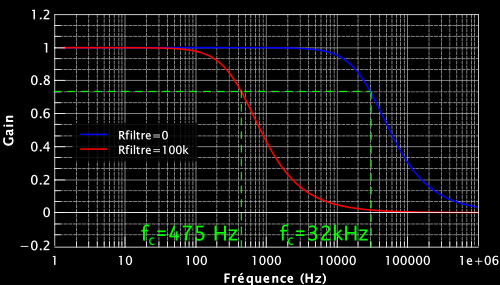
Pour $R_{filtre}$=0 :

$f_c=\Large \frac{1}{2\times 3,14 \times (0+1,5k)\times 3,3n}=$32 kHz

Pour $R_{filtre}$=100 kohms :

$f_c=\Large \frac{1}{2\times 3,14 \times (100k+1,5k)\times 3,3n}$=475 Hz

Par conséquent, lorsque $R_{filtre}$ est nul, on laisse passer tous les aigus possibles. Lorsque $R_{filtre}$ est maximal, on ne laisse passer que les fréquences inférieures à 475 Hz. On filtre donc beaucoup d’aigus !

Voici le graph qui correspond au calcul :

3 Mise en pratique : montage d’un filtre RC passif

Vous pouvez consulter une vidéo sur le montage pas-à-pas du filtre RC sur protoboard en cliquant ici.

4 Concusion et perspectives

Dans cet article nous avons abordé l’étude formelle d’un filtre RC passif, que l’on peut inclure facilement dans une pédale d’effet.

Le circuit de la RAT contient également un transistor en sortie du filtre, qui est monté en drain commun. Il agit comme un buffer, et on peut le considérer comme faisant partie du circuit filtrage. Il aide à ce que le filtre agisse comme on le prédit par le calcul, en adaptant l’impédance en sortie.

Une étude systématiques des filtres se fait en regardant leur gabarit, leur fonction de transfert et leur diagramme de Bode. Ainsi on détermine les différentes fréquences de coupure, la bande passante, la qualité du filtre, son ordre, la réponse en gain et en fréquence, etc…

Vous avez des questions ? N’hésitez pas à les poser en commentaires !