Les nombres complexes peuvent paraître une fantaisie inventée par les mathématiciens. Mais il n’en n’est rien : en contrôlant cet outil, la résolution dans notre cas de circuit électriques est beaucoup plus facile.
Par exemple, pour résoudre un simple filtre passe haut, composé d’une résistance et d’un condensateur, vous pouvez utiliser les nombres « réels » qui sont ceux que l’on utilise dans la vie de tous les jours. Il faut alors utiliser des fonctions sinus, cosinus et tout devient compliqué (voir l’article sur la réactance et alternative aux nombres complexes).
Ou vous pouvez franchir le pas, apprendre ce formalisme, et la résolution se fait alors en quelques lignes (voir par exemple l’article sur la perte d’aigus du micro guitare).
Dans cet article, je vais donner des bases sur les nombres complexes. Ces bases sont suffisantes pour comprendre l’étude de filtres que nous verrons ailleurs. Je proposerai également un article plus poussé sur les nombres complexes prochainement, histoire d’y aller pas à pas.
Attention : cet article n’a pas la prétention d’être rigoureux du point de vue mathématique, je fais volontairement pas mal de raccourcis pour aller au but.
Sommaire
1 Définition générale des nombres complexes
1.1 Définition de $j$
La notion de nombres s’est enrichie au cours des siècles. Un exemple de nombres « spéciaux » sont les entiers naturels. Ils regroupent les nombres entiers positifs et zéro : 0, 1, 2, 3… On appelle tous ces nombres un ensemble [1], celui-ci s’appelle donc l’ensemble des entiers naturels et se note $\mathbb{N}$.
D’autres exemples : l’ensemble des entiers relatifs (noté $\mathbb{Z}$) regroupe les nombres entiers positifs, négatifs et nul : …-3, -2, -1, 0, 1, 2, 3…
L’ensemble des nombres réels (noté $\mathbb{R}$ ) regroupe en plus les nombres décimaux, par exemple 2,356 ; $\pi$; $\sqrt{2}$,…).
Les nombres complexes sont un ensemble encore plus large : celui-ci regroupe les nombres dont le carré est négatif !
Pourquoi les a t’on inventé ? Ils ont été entrevus au XVIe siècle pour la résolution d’équations. Au XVIIIe siècle, Leonhard Euler désigne le nombre complexe dont le carré vaut -1, il l’appelle $i$. Ainsi : $i^2=-1$. $i$ est le nombre imaginaire.
En électronique cependant, vu qu’on utilise $i$ pour désigner le courant, on utilise la lettre $j$ et on a donc $j^2=-1$.
1.2 Écriture d’un nombre complexe
Un nombre complexe $z$ peut s’écrire de plusieurs manières. La manière la plus simple est de l’écrire sous la forme $z=a+j\times b$. $a$ et $b$ sont des réels quelconques, $j$ est le nombre complexe tel que $j^2=-1$. Dans la suite, on omettra le symbole $\times$ entre $j$ et $b$.
Par conséquent, on voit que si $b=0$, $z=a$ et donc $z$ est un nombre réel car $a$ est un nombre réel.
Si maintenant $a=0$, $z=jb$. $z$ n’a plus de partie réelle et $z$ est maintenant ce qu’on appelle un imaginaire pur (ou complexe pur).
La forme $z=a+jb$ s’appelle la forme algébrique.
Retenons (et admettons) jusqu’ici que :
- Il existe un ensemble appelé ensemble des nombres complexes, noté $\mathbb{C}$ qui contient l’ensemble des nombres réels $\mathbb{R}$.
- Les mêmes règles de calcul sont valables que dans $\mathbb{R}$
- Dans $\mathbb{C}$, il existe un nombre $j$ tel que $j^2=-1$
- Tout nombre complexe $z$ peut s’écrire sous la forme unique $z=a+jb$ avec $a$ et $b$ des nombres réels. $a$ s’appelle la partie réelle de $z$, $b$ s’appelle la partie imaginaire de $z$.
1.3 Représentation géométrique d’un nombre complexe
Avec la représentation géométrique, tout va s’éclairer davantage ! En regardant la forme algébrique de $z$, on voit que $z$ est défini par deux composantes, la composante réelle et la composante imaginaire. On peut donc le représenter sur la feuille (ou l’écran), en dessinant deux axes. L’axe des abscisses porte la partie réelle, et l’axe des ordonnées la partie imaginaire.
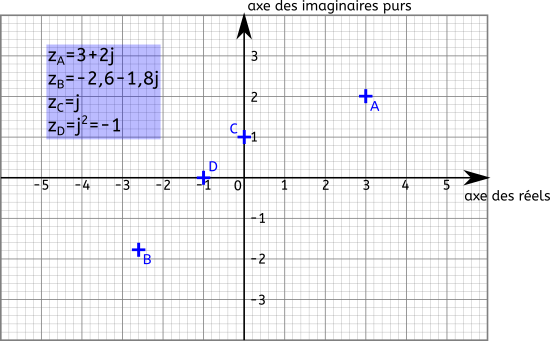
Sur ce graph nous avons placé 4 points. Le point $A$ représente le nombre complexe $z_A=3+2j$. On le place donc de manière a ce qu’il ait une abscisse de 3 et une ordonnée de 2.
Le point $B$ représente le nombre complexe $z_B=-2,6-1,8j$. Vu que sa partie réelle et sa partie imaginaire sont négatives, il se trouve à l’opposé du point $A$.
Les points $C$ et $D$ sont des cas particuliers. $z_C=j$, $z_C$ est donc un imaginaire pur, c’est même le nombre imaginaire. Ses coordonnées sont donc (0;1).
Le point $D$ est tel que $z_D=j^2$ or $j^2=-1$ donc $z_D=-1$. Par conséquent, les coordonnées du nombre $j^2$ sont (-1;0). $j^2$ est un nombre réel négatif.
Voilà, je pense qu’à travers ces exemples vous voyez un peu mieux ce qu’est un nombre complexe. C’est un nombre à deux dimensions, qui englobe l’axe des nombres réels (l’abscisse de la figure ci-dessus) auquel on a rajouté une 2e dimension.
Avant de voir à quoi nous servent les nombres complexes, nous devons voir quelques règles de calcul.
2 Règles de calcul sur les nombres complexes
On peut ajouter, soustraire, multiplier et diviser des nombres complexes (dans ce dernier cas, on s’assurera que le nombre complexe du dénominateur n’est pas nul).
2.1 Propriétés
Soit $z$ et $z’$ deux nombres complexes tel que $z=a+jb$ et $z’=a’+jb’$. Alors :
$
\begin{array}{lll}
z+z’ &=& a+jb+a’+jb’ \\
&=& a+a’ + j(b+b’)
\end{array}
$
On remarque que l’on range ensemble les nombres qui ne portent pas de $j$ et ceux qui portent un $j$. La partie réelle de $z+z’$ est $a+a’$, sa partie imaginaire est $b+b’$.
$
\begin{array}{lll}
z \times z’ &=& (a+jb)(a’+jb’) \\
&=& aa’ + jab’ + jba’ + j^2bb’ \\
&=& aa’ – bb’ +j(ab’+ba’)
\end{array}
$
$
\begin{array}{lll}
kz &=& k(a+jb) \\
&=& ka + jkb
\end{array}
$
Par conséquent, une opération sur deux nombres complexes donne un nouveau nombre complexe. En factorisant par $j$, on met en évidence quelle est la partie réelle du nouveau nombre complexe, et quelle est sa partie imaginaire.
2.2 Inverse d’un nombre complexe et quantité conjuguée
Interessons nous maintenant à l’inverse d’un nombre complexe. Pour cela, on définit la quantité conjuguée d’un nombre complexe notée avec une barre : $\bar{z}$. Si $z=a+jb$, alors $\bar{z}=a-jb$. La quantité conjuguée se définit en prenant l’opposé en signe de la partie imaginaire.
Si on multiplie un nombre complexe par sa quantité conjuguée, on trouve un nombre réel (il n’y a plus de $j$) :
$
\begin{array}{lll}
z\times \bar{z} &=& (a+jb)(a-jb) \\
&=& a^2 +jab -jba -j^2b^2 \\
&=& a^2 +b^2
\end{array}
$
Revenons alors à l’inverse d’un nombre complexe :
$
\begin{array}{lll}
\displaystyle \frac{1}{z} &=& \displaystyle \frac{1}{a+jb}\\
&=& \displaystyle \frac{a-jb}{(a+jb)(a-jb)} \\
&=& \displaystyle \frac{a-jb}{a^2+b^2}
\end{array}
$
On a multiplié en haut et en bas par $\bar{z}$, ce qui permet de faire disparaître $j$ au dénominateur, et donc de trouver que la partie réelle de $ \displaystyle \frac{1}{z}$ vaut $ \displaystyle \frac{a}{a^2+b^2} $ et la partie imaginaire vaut $ \displaystyle \frac{-b}{a^2+b^2} $.
2.3 Une autre propriété intéressante
$
\begin{array}{lll}
\displaystyle \frac{1}{j} &=& \displaystyle \frac{j}{j^2} \\
&=& \displaystyle \frac{j}{-1} \\
&=& -j
\end{array}
$
On a multiplié en haut et en bas par $j$ pour l’éliminer dans le dénominateur. On trouve donc que $ \displaystyle \frac{1}{j}=-j$.
3 Module et argument d’un nombre complexe
Soit $z$ un nombre complexe tel que $z=a+jb$ avec $a$ et $b$ deux nombres réels quelconques. Plaçons le point $M$ associé au nombre complexe $z$ :
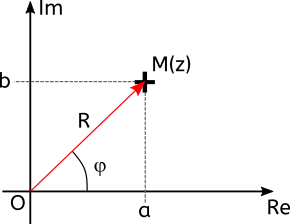
Le point $M$ a donc pour coordonnées ($a$;$b$). On peut aussi définir les coordonnées du point $M$ par sa distance $R$ avec l’origine $O$ et l’angle $\varphi$ que fait le vecteur $\overrightarrow{OM}$ avec l’axe des abscisses. $R$ s’appelle le module de $z$ et se note $|z|$. On appelle $\varphi$ l’argument de $z$, que l’on note $arg(z)$.
Il est donc possible d’exprimer un nombre complexe en fonction de son module et de son argument. En utilisant le théorème de de pythagore et la formule de la tangeante, on trouve que :
$$
R=\sqrt{a^2 + b^2} \\
\tan \varphi=\frac{b}{a}
$$
Un exemple :
Si $z=-5+3j$, $R=|z|=\sqrt{(-5)^2+3^2}=\sqrt{34}$. Et $\tan \varphi=arg(z)=\frac{3}{-5}$ donc $\varphi=arctan(\frac{3}{-5})\simeq-31º$
En pratique, le module sera associé à l’amplitude d’un signal et l’argument à son déphasage.
4 Définition de l’impédance complexe
Nous avons vu dans l’article sur la réactance que lorsque l’on est en régime alternatif, un condensateur ou une bobine vont empêcher le courant de passer, en raison de leur réactance. La réactance est un nombre réel qui dépend de la fréquence du signal. Rappelons qu’en régime sinusoïdal la réactance vaut $\displaystyle \frac{1}{\omega C}$ pour un condensateur et $\omega L$ pour une bobine.
Or, les calculs d’impédance équivalente avec les nombres réels sont assez compliqués, il faut prendre en compte les déphasages. Cependant en utilisant les nombres complexes, l’information sur le déphasage est présente dans ce nombre. Nous n’allons pas expliquer pourquoi ici, nous y reviendrons dans un prochain article plus poussé sur les nombres complexes. Mais on peut avoir une intuition de cela : les nombres réels ont une seule dimension, alors que les nombres complexes en ont deux. Un nombre complexe peut donc contenir l’information sur deux quantités comme l’amplitude et le déphasage d’une onde sinusoïdale.
Supposons que notre signal est sinusoïdal. Avec les nombres complexes on définit les impédances complexes, pour une capacité :
$$ z_C= \frac{1}{j\omega C} $$
et pour une inductance :
$$ z_L= j \omega L $$
On voit qu’on a des formes très proches des réactances, mais ce sont des nombres complexes car il y a le nombre $j$.
Dans l’article sur le micro de guitare électrique et la perte d’aigus, le 3e paragraphe donne un exemple d’utilisation de l’impédance complexe en modélisant le micro de la guitare par une bobine. Le calcul permet de trouver la fréquence de coupure du filtre que forment la bobine et la résistance d’entrée de l’ampli, et donc de savoir quelles fréquences aiguës sont coupées.
5 Conclusion et perspectives
Dans cet article, bien qu’ayant effleuré les bases sur les nombres complexes, nous avons pu voir un bon aperçu de ce qu’ils sont. Ces bases vont nous servir à calculer par exemple la fonction de transfert d’un filtre pour calculer le gain en tension et le déphasage du signal de sortie.
D’autres notions sont intéressantes comme la notation trigonométrique ou exponentielle, qui permettent de faciliter le maniement des nombres complexes dans les calculs en utilisant les propriétés mathématiques des puissances. Mais, ce sera pour une prochaine fois !
Vous avez aimé cet article ? N’hésitez pas à le partager !
Références
[1] https://fr.wikipedia.org/wiki/Ensemble_de_nombres