
Cet article est un peu velu et je m’en excuse. Ce que j’ai voulu faire, c’est expliquer les filtres, l’impédance, la réactance sans faire appel aux nombres complexes. Que sont les nombres complexes ? C’est un outil mathématique extrêmement utile. Ce sont des nombres qui ont deux dimensions : une partie réelle et une partie imaginaire, ou un module et un angle.
Cependant, comprendre les nombres complexes requiert un certain investissement en temps [1]. On peut alors obtenir facilement beaucoup de choses, comme le gain d’un filtre, son évolution en fréquence, et bien plus.
En général, dans les livres ou sur le net, même pour un circuit simple comme le circuit RC série, la résolution se fera en utilisant les nombres complexes. Ou alors on donnera les formules d’impédance et de réactance sans justification. En fait je n’ai pas pu trouver d’explication sur l’origine de ces formules autre que par l’utilisation des nombres complexes.
Et je me suis dit qu’il serait intéressant d’aborder les circuits simple en régime alternatif avec des maths que l’on voit au collège : dans cet article vous pourrez lire les noms de Pythagore, Chasles, et les mots vecteurs, trigonométrie, colinéarité, même s’il y a aussi une dérivée à un moment.
Et au final ça marche, on obtient les même résultats qu’en utilisant les nombres complexes (heureusement !). Cependant, même si les concepts mathématiques sont de niveau collège, la lecture de cet article pourra sembler fastidieuse, donc accrochez vous !
Avec le diagramme de Fresnel, vous pourrez étudier des circuits simples sans faire appel aux nombres complexes, je pense donc qu’il est utile de connaître leur construction.
Notons finalement que je ne résous ici que le cas du circuit RC, vu que l’article est déjà long.
Sommaire
1 Contexte
Lorsque le signal de la guitare passe à travers une pédale, il sort avec une amplitude différente et pourra également être déphasé (si la pédale est allumée bien entendu !).
Le signal de la guitare est un signal complexe, que l’on peut décomposer en une somme de sinusoïdes (cela s’appelle faire une transformée de Fourrier).
Nous allons donc supposer que le signal S de la guitare est composée d’une seule sinusoïde, de fréquence f et d’amplitude A. S varie avec le temps, on le note donc S(t).
S(t) est donc de la forme : $S(t) = A \sin(2\pi f t )$.
Rappelons que pour un signal sinusoïdal, l’amplitude est donnée par le facteur multiplicatif devant le sinus, et la fréquence est dans l’argument du sinus.
Notons également que lorsque l’on utilise les fonctions trigonométrique, on aime parler en pulsation plutôt qu’en fréquence. La pulsation se note $\omega$, et la fréquence et la pulsation sont liées par la relation $\omega=2\pi f$. Par conséquent :
$\displaystyle S(t)=A \sin(\omega t)$.
Imaginons maintenant que le signal de sortie S’ ait une amplitude différente, que l’on note A’ et soit déphasée par rapport au signal d’entrée d’une quantité $\phi$. Sa pulsation est conservée.
Physiquement, le déphasage signifie que la nouvelle sinusoïde atteint son maximum à un autre moment que la première. Le déphasage est un angle et entre donc dans l’argument de la fonction sinus. Par conséquent, le signal de sortie est de la forme :
$\displaystyle S'(t)=A’ \sin(\omega t + \phi)$.
Voici un exemple de représentation graphique des deux fonctions :
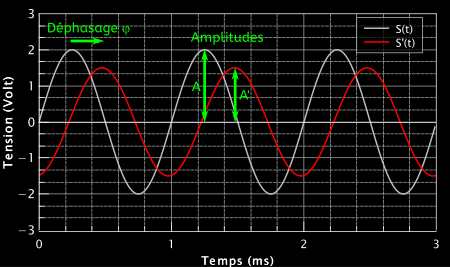
L’objectif est de connaître les caractéristiques du signal de sortie A’ et φ connaissant celles d’entrée A et f.
2 Là où ça se complique
2.1 Circuit RC simple
Supposons que notre guitare est un générateur de tension sinusoïdal, et qu’elle est connectée à une pédale qui contient une résistance et un condensateur en série.
Ce genre de circuit est un filtre RC. Voici le schéma électrique :
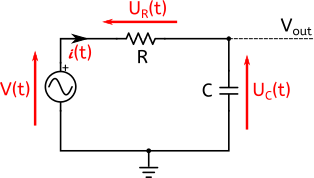
V(t) est le signal d’entrée, connu. Supposons que son amplitude soit Vm et sa pulsation ω.
$\displaystyle V(t)=V_m sin (\omega t)$
Or, puisque nous avons un régime sinusoïdal forcé (par le générateur), on peut montrer qu’au bout d’un certain temps (qui n’est pas nécessairement grand) les tensions et le courant oscilleront de manière sinusoïdale à la fréquence du générateur.
Vout est la tension de sortie du filtre. C’est également la tension Uc aux bornes du condensateur. Soit Ucm son amplitude et φ le déphasage crée. Par conséquent :
$\displaystyle U_c(t)=U_{cm} sin (\omega t + \phi)$
Nous cherchons à déterminer Ucm et φ connaissant V(t), R et C.
2.2 Détermination du courant i(t)
Nous avons déjà fait ce calcul dans ce blog, mais nous allons le refaire ici. Si vous avez des difficultés, vous pouvez consulter cet article sur les dérivées.
Le courant est défini par la variation de charge dans le temps :
$\displaystyle i=\frac{dq}{dt}$
Et dans un condensateur, la quantité de charge stockée dépend de la tension à ses bornes Uc et de sa capacité C :
$\displaystyle q=C\times U_c$
En utilisant ces deux équations on obtient que :
$\displaystyle i(t)=\frac{dq}{dt}=C \frac{dU_c}{dt} =C \omega U_{cm} \cos (\omega t + \phi)$
Or on sait que cos x = sin (x+ π/2) ( π est un angle de 180º. Par conséquent un tour, soit 360º correspondent à 2 π, et π /2 correspond à 90º).
On peut donc remplacer le cosinus de i(t) par un sinus et on trouve :
$\displaystyle i(t)= \omega C U_{cm} \sin \left(\omega t + \phi + \frac{\pi}{2}\right)$
On voit apparaître un déphasage de +90º entre le courant i(t) et la tension aux bornes du condensateur Uc. Le courant est donc en avance de 90º sur la tension.
2.3 Détermination de UR(t)
Ici, c’est facile. R est une résistance, on applique la loi d’Ohm :
$\displaystyle U_R(t)=R\times i(t)$
Et on remplace i(t) par l’expression que l’on a trouvé :
$\displaystyle U_R(t)=R \omega C U_{cm} \sin \left(\omega t + \phi + \frac{\pi}{2}\right) $
2.4 Loi des mailles
On peut dès lors appliquer la loi des mailles, et obtenir une équation pour trouver Ucm et φ.
La loi des mailles nous dit que :
$\displaystyle V(t)=U_c(t)+U_R(t)$
Jusque là, tout va bien.
Là où ça se gâte, c’est que les tensions dépendent du temps, selon une sinusoïde. Remplaçons chacune des tensions par leur expression :
$\displaystyle V_m sin (\omega t) = U_{cm} sin (\omega t + \phi) + R C \omega U_{cm} \sin \left(\omega t + \phi + \frac{\pi}{2}\right) $
On a bien une expression qui nous donne nos deux inconnues, Ucm et φ en fonction de tous les autres paramètres (connus), mais il est compliqué de les sortir de là par le calcul.
Il est donc temps d’appeler un ami… Et cet ami, c’est Monsieur Fresnel.
3 Représentation de Fresnel
3.1 Définition des vecteurs
Le problème de l’équation précédente réside dans les déphasages qui se trouvent dans l’argument du sinus.
Lorsque l’on ne travaille qu’avec des résistances, aucun déphasage n’est induit et nous n’avons qu’une seule inconnue. Même si le régime est sinusoïdal, on peut factoriser par les sinus et le calcul se fait plutôt bien.
Mais ici, nous avons deux inconnues, l’amplitude et la phase. Nous avons cependant un outil mathématique très utile pour nous aider : les vecteurs.
À chaque grandeur sinusoïdale nous allons lui associer un vecteur dont:
- le module est l’amplitude de la sinusoïdale.
- l’angle avec une droite de référence – l’axe des abscisses par exemple – est la phase de la sinusoïdale.
3.2 Représentation vectorielle de V(t), Uc(t), UR(t) et i(t)
Nous allons représenter vectoriellement V(t), Uc(t), UR(t) et i(t). Nous avons posé que :
- $\displaystyle V(t)=V_m sin (\omega t)$
- $\displaystyle U_c(t)=U_{cm} sin (\omega t +\phi)$
Et nous avons trouvé que :
- $\displaystyle i(t)= \omega C U_{cm} \sin \left(\omega t + \phi + \frac{\pi}{2}\right)$
- $\displaystyle U_R(t)= \omega R C U_{cm} \sin \left(\omega t + \phi + \frac{\pi}{2}\right) $
Ainsi :
- à V(t) on associe un vecteur $\vec{V}$ de module Vm et colinéaire avec l’axe des abscisses.
- à Uc(t) on associe un vecteur $\vec{U_c}$ de module Ucm faisant un angle φ avec l’axe des abscisse.
- i(t) est associé à un vecteur $\vec{i}$ de module ωCUcm faisant un angle φ + π /2 avec l’axe des abscisses.
- à UR(t) on associe un vecteur $\vec{U_R}$ de module ωRCUcm faisant un angle φ + π /2 avec l’axe des abscisses.
$\vec{U_R}$ et $\vec{i}$ sont donc colinéaires et il y a un angle droit entre $\vec{U_c}$ et $\vec{i}$
Voilà la représentation des vecteurs $\vec{i}, \vec{U_c}$ et $\vec{U_{R}}$ :
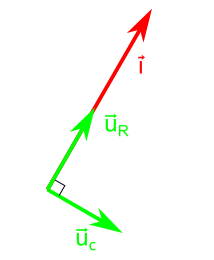
On considère que ces vecteurs tournent autour de l’origine à la pulsation ω, ce qui revient à les considérer fixes sur le papier.
Cas de V(t)
Il ne nous reste plus qu’à représenter le vecteur $\vec{V}$, qui va nous aider à trouver φ et Ucm.
En effet, nous savons par la loi des mailles que :
$\vec{V} = \vec{U_c} + \vec{U_R} $
En appliquant la relation de Chasles [2], nous pouvons donc représenter tous les vecteurs. Pour rendre les choses plus faciles, nous allons mettre le courant horizontal. Voici ce que donne le diagramme, en complétant la construction de la figure du dessus :
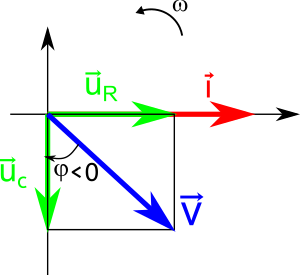
3.3 Résolution du problème : expressions de Ucm et de φ
Il ne reste maintenant plus qu’à utiliser nos « vieilles » formules de collège : théorème de Pythagore [3] et trigonométrie [4] !
Avec le théorème de Pythagore nous allons travailler sur le module (la longueur) des vecteurs. Le module, que l’on note entre deux barres verticales, est donné par tout ce qu’il y a devant le sinus. Ainsi :
$|\vec{V}|=V_m$
$|\vec{U_c}|=U_{cm}$
$|\vec{U_R}|=\omega R C U_{cm} $
$|\vec{i}|= \omega R C U_{cm} $
On utilise le théorème de Pythagore :
$\displaystyle V_m^2=U_{cm}^2+ (\omega R C U_{cm} )^2$
$\displaystyle \Rightarrow V_m^2=U_{cm}^2(1 + (\omega R C )^2 )$
$\displaystyle \Rightarrow V_m=U_{cm} \sqrt{(1 + (\omega R C )^2 )}$
Et on réécrit ça pour trouver l’expression de Ucm :
$\displaystyle \boxed{ U_{cm} =\frac{V_m}{\sqrt{(1 + (\omega R C )^2 )}} }$
Voici son évolution avec la fréquence :
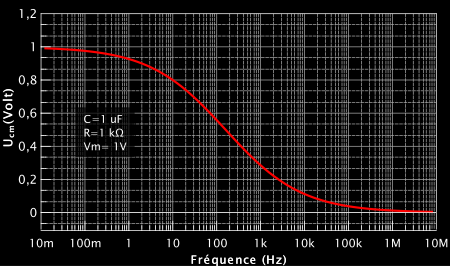
On constate que la tension aux bornes du condensateur est égale à la tension du générateur à basse fréquence, et tend vers 0 à haute fréquence. Nous avons donc crée un filtre passe-bas.
Notons que l’on comprends cela intuitivement, car vu que le condensateur se comporte comme un fil à haute fréquence, la tension à ses bornes est nulle !
Il nous reste à trouver la phase. Pour cela on utilise l’expression de la tangente qui est égale au rapport entre le côté opposé et le côté adjacent [4] :
$\displaystyle \tan \phi =-\frac{\omega RCU_{cm}}{U_{cm}}$
$\displaystyle \Rightarrow \tan \phi =-\omega RC$
Le signe « – » est dû au fait que φ est négatif. Par conséquent, en utilisant la fonction réciproque de la tangente on trouve :
$\displaystyle \boxed{ \phi =\arctan(-\omega RC)}$
4 Définition de la réactance
4.1 Réactance d’un condensateur
Si on note im l’amplitude de i(t), on trouve que :
$i_m= \omega C U_{cm} $
C’est à dire :
$\displaystyle U_{cm}= \frac{1}{\omega C} i_m $
En comparant avec la loi d’Ohm, nous identifions la quantité $\displaystyle \frac{1}{\omega C}$ comme étant équivalente à une résistance. On l’appelle la réactance et on la note souvent Xc ou Rc. Son unité est l’ohm.
$\displaystyle \boxed{X_c=\frac{1}{\omega C}}$
Pour un circuit capacitif, la réactance sera donc l’équivalent de la résistance pour un circuit résistif.
On voit de plus que la réactance dépend de la pulsation de la fréquence d’entrée. Plus la pulsation est grande, plus la réactance sera petite.
Par conséquent, cela signifie qu’un condensateur réagit à la circulation du courant alternatif, en opposant une réactance d’autant plus grande que la fréquence est faible.
Dans le cas d’une tension continue, la fréquence est nulle, et par conséquent la réactance est infinie. On retrouve bien qu’un condensateur ne laisse pas passer le courant continu.
Sur la figure suivante, j’ai représenté la réactance d’un condensateur de 1 uF de capacité :
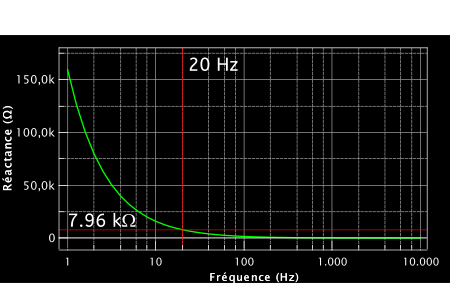
On peut calculer la réactance du condensateur à 20 Hz par exemple :
$\displaystyle X_c=\frac{1}{\omega C}=\frac{1}{2\pi \times 20 \times 1000\times 10^{-9}}\simeq 7,96 k\Omega$
4.2 Réactance d’une bobine
On peut de même trouver l’expression de la réactance XL d’une bobine d’inductance L à l’aide de l’expression reliant courant et tension UL de la bobine :
$\displaystyle U_L=L \frac{di}{dt}$
On trouve que :
$\displaystyle \boxed{X_L=\omega L}$
On peut également démontrer que le vecteur $\vec{U_L}$ pointe vers le haut.
Je vous laisse le démontrer, c’est exactement les mêmes calculs que ceux vus plus haut. S’il y a un problème, dîtes le moi dans les commentaires !
5 Expression de l’impédance totale du circuit
En utilisant la représentation de Fresnel, on n’a plus à utiliser tout le formalisme précédant. On représente pour un circuit série le courant horizontal vers la droite. Le module des vecteurs est celui de la résistance ou de la réactance. Et en fonction du composant la flèche pointera vers le bas, le haut ou la droite.
En sommant les vecteurs, on trouve un nouveau vecteur. Son module est l’impédance totale du circuit, l’angle qu’il fait avec le composant de sortie est la phase. On déduit aussi la tension de sortie.
Rappelons que impédance est le terme général qui tient en compte les résistances et les réactances, et s’exprime donc également en ohms.
Voici la représentation de Fresnel du circuit RC en impédance :
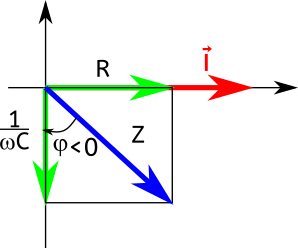
On applique le théorème de Pythagore dans le triangle rectangle qui contient φ et on trouve :
$\displaystyle Z^2=R^2+\left(\frac{1}{\omega C}\right)^2$
On trouve donc l’expression de l’impédance Z :
$\displaystyle \boxed{Z=\sqrt{R^2+\left(\frac{1}{\omega C}\right)^2}}$
Note : On voit que Z n’est pas la somme de R et de Xc. Encore une fois, ceci est dû au déphasage causé par le condensateur.
6 Résolution simplifiée du problème
On utilise alors la formule du pont diviseur de tension pour trouver la tension de sortie et retrouver les résultats vus plus haut.
$\displaystyle V_{out}=U_{cm}=V_i\times\frac{X_c}{Z}=V_i\times \frac{\frac{1}{\omega C}}{\sqrt{R^2+\left(\frac{1}{\omega C}\right)^2}}$
Donc :
$\displaystyle V_{out} = V_i\times \frac{1}{\sqrt{1+(\omega RC)^2}}$
Et la phase est négative, on met donc un signe « – » et on a :
$\displaystyle \tan \phi = -\frac{R}{\frac{1}{\omega C}}=-\omega RC$
Donc :
$\phi=\arctan(-\omega R C)$
Si ce qui nous intéresse est l’étude de ce filtre, on représentera le gain (égal au rapport entre tension de sortie et tension d’entrée) et la phase en fonction de la pulsation. On déterminera également la fréquence de coupure.
Résumé et perspectives
Dans cet article, nous avons vu le formalisme mathématique qui nous permet de justifier une représentation en vecteurs et leur orientation. À l’aide du diagramme de Fresnel, nous pouvons trouver les caractéristiques de la tension aux bornes du composant voulu et sa phase par rapport à la tension d’entrée.
Ceci est très utile pour l’étude de filtres par exemple. Le circuit RC du début est un filtre passe bas. Il nous resterait à étudier son gain en fréquence et sa fréquence de coupure.
Une fois l’outil de la représentation de Fresnel connu, on peut l’appliquer à d’autres circuits simples comme les circuits CR, RL, LR, RLC.
Pour des circuits plus compliqués il faudra utiliser les nombres complexes. Ce sont des nombres à deux dimensions, qui sont donc comparables à l’utilisation des vecteurs, avec le formalisme des puissances en plus. C’est un outil qui demande de l’investissement en temps mais qui facilite énormément la tâche pour l’analyse de circuits ensuite. La résolution d’un circuit RL utilisant les nombres complexes a déjà été traité dans l’article sur le micro de guitare. Nous y reviendrons prochainement !
Si vous avez des questions, n’hésitez pas à les poser en commentaires !
Références
[1] P. Horowitz and W. Hill, The art of electronics p.31, Cambridge University Press
[2] https://fr.wikipedia.org/wiki/Vecteur
[3] https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_de_Pythagore
[4] https://fr.wikipedia.org/wiki/Trigonom%C3%A9trie

Ping : Les nombres complexes : bases - Fais-tes-effets-guitare.com