Résistance d'entrée/sortie et effet sur l'amplitude du signal transmis

Vous avez peut-être lu ou entendu dire que la résistance d’entrée de votre ampli doit être bien plus grande que la résistance de sortie de votre source (le micro de votre guitare en l’occurrence). Pire, on vous a parlé d’impédance. Mais pourquoi ? Que se cache derrière ces concepts barbares ? Et surtout, quelle conséquences ont ils sur notre son ?

La motivation de cet article est également de répondre aux questions que m’a posé l’un de vous. Chers lecteurs, merci pour votre intérêt ! 🙂

Je vais donc vous expliquer tout cela, en plusieurs articles, parce qu’il y a beaucoup à dire, et comme ça je peux expliquer les choses tranquillement.

Dans un premier temps, nous nous assurerons de bien comprendre ce qu’est le signal audio.

Puis nous modéliserons le micro de la guitare et l’amplificateur par des résistances et des sources de tension. Ce modèle simple permettra de comprendre l’effet des résistances d’entrée/sortie sur l’amplitude du signal.

Finalement le concept d’impédance sera introduit. Nous aborderons intuitivement comment l’impédance du micro de la guitare en conjonction avec l’impédance d’entrée qui le suit est un circuit qui bouffe les aigus.

Sommaire

1 Du micro au haut-parleur : histoire d’onde

Que fait un micro guitare ? Il transforme la vibration d’une corde en vibration électrique.

La vibration d’une corde, en physique on appelle cela une onde de type mécanique.

Par conséquent, un micro transforme une onde mécanique en onde électrique.

Fréquence de l’onde

Micro Humbucker Gibson — Micro humbucker.

Le micro va essayer au maximum de reproduire électriquement les caractéristiques de l’onde mécanique. Si vous jouez un « la 440 » à la guitare, la corde vibre essentiellement à 440 Hz. Cela veut dire que la corde fait 440 oscillations par seconde (on néglige les harmoniques produites).

Plus le nombre d’oscillations par seconde est grand, plus la fréquence est grande et plus la note est aiguë.

Par conséquent, le son produit par un moustique au vol nous indique qu’il bat des ailes plus vite qu’un bourdon…

Notre micro guitare doit transmettre ce « la 440 » de manière électrique. Les 440 oscillations par seconde de la corde de la guitare vont se transformer en 440 oscillations par seconde de la tension aux bornes du micro, comme l’illustre la figure suivante :

Un "la" 440, représenté sur la portée correspond à 440 battements par seconde. On l'a représenté ici par une onde de forme sinusoïdale. — Un « la 440 », représenté sur la portée correspond à 440 battements ou oscillations par seconde. On l’a représenté ici par une onde de forme sinusoïdale.

Par conséquent, il faut bien comprendre qu’un signal audio est un signal électrique alternatif : qui oscille autour d’une valeur nulle. Ce n’est pas un signal continu (de valeur constante)

En branchant un câble au micro et en le reliant à un amplificateur, l’oscillation électrique va se propager jusqu’à l’ampli. L’ampli va, je vous le donne en mille, amplifier ce signal. Le but est de mettre en mouvement la membrane du haut parleur qui va mouvoir l’air ambiant à 440 oscillations par seconde. Le résultat est qu’on retrouve une onde mécanique, mais beaucoup plus intense que celle crée à la guitare.

Autrement dit, on entend de nouveau un « la », mais bien plus fort.

Amplitude de l’onde

L’autre aspect important à considérer est l’amplitude du son. Lorsqu’on joue fort à la guitare, le micro traduit cela par une onde électrique de plus grande amplitude.

2 Modélisation simple : résistance d’entrée et de sortie d’une source et d’un amplificateur

2.1 Cas de la source : signal de la guitare

Vous l’avez compris, le signal audio est un signal électrique alternatif.

Les personnes qui ont lu cet article ont aussi lu : Tone sucking et buffers

Pour modéliser le signal de la guitare, on va considérer que l’oscillation est de forme sinusoïdale (voir l’article les générateurs de tension, courant et formes du signal pour plus de détails sur les différentes formes de signal). En réalité la forme du son est plus complexe, mais nous n’en avons pas besoin ici.

On modélise donc simplement le signal de la guitare par un générateur de tension sinusoïdal.

Mais si on veut savoir quelle quantité de signal entre réellement dans l’ampli, on va devoir considérer également la résistance interne ou de sortie du micro. Je l’appelle ici Rs (le « s » va pour source).

Voici donc le modèle du micro guitare que l’on va considérer en 1ère approche :

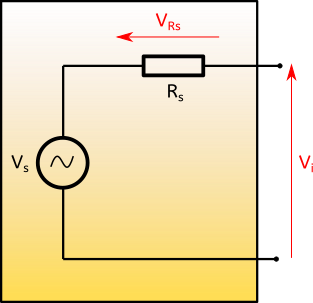
1ère approximation d'un micro de guitare électrique. Vs est la tension alternative sinusoïdale délivrée par le micro guitare, Rs est la résistance interne du micro et Vi est la tension que l'on mesure aux bornes du micro. — 1ère approche d’un micro de guitare électrique. Vs est la tension alternative sinusoïdale délivrée par le micro de la guitare, Rs est la résistance interne du micro et Vi est la tension que l’on mesure aux bornes du micro.

La tension que le micro délivre est V_s, mais la tension envoyée à l’ampli est V_i, inférieure, car on ne peut faire fi de la résistance interne R_s. Celle-ci fait chuter la tension d’une quantité que l’on va déterminer dans la suite.

2.2 Modèle de l’amplificateur

Lorsque vous branchez la guitare à l’ampli, le micro de votre guitare va voir une résistance de charge, concrètement celle de la résistance d’entrée de votre ampli.

La valeur de la résistance de sortie du micro et celle d’entrée de l’ampli vont avoir deux conséquences :

une sur la quantité de signal qui va entrer dans l’ampli
une sur la réponse tonale de l’ensemble guitare + ampli, que nous verrons succinctement à la fin, et plus en détails dans un autre article.

Afin de voir l’effet de ces deux résistance, on va modéliser un ampli de la façon suivante. C’est un modèle simple, mais largement suffisant pour expliquer ce qui suit.

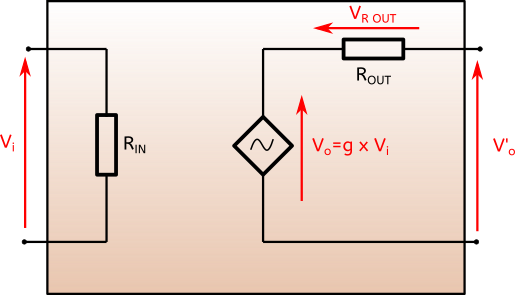
Modèle de l'amplificateur. Rin symbolise sa résistance d'entrée, Rout sa résistance de sortie. L'amplificateur amplifie en interne la tension qu'on lui soumet d'un facteur g. Il délivre donc en interne une tension qui vaut g x Vi, mais en raison de la présence d'une résistance interne de sortie Rout, la tension délivrée à l'extérieur est plus petite, elle est notée V'o. — Modèle de l’amplificateur. Rin symbolise sa résistance d’entrée, Rout sa résistance de sortie. L’amplificateur amplifie en interne la tension qu’on lui soumet d’un facteur g. Il délivre donc en interne une tension qui vaut g x Vi, mais en raison de la présence d’une résistance interne de sortie Rout, la tension délivrée à l’extérieur est plus petite, elle est notée V’o.

Ce modèle est très simple : R_IN représentante la résistance d’entrée de l’ampli. Cette résistance d’entrée dépend du circuit utilisé pour l’amplification. Par exemple, ce ne sera pas la même chose si on a en entrée un buffer dont le rôle est d’adapter l’impédance, ou un transistor monté en émetteur commun par exemple. Mais ne nous affolons pas, retenons juste que notre ampli a une résistance d’entrée, due au circuit qui le compose.

La sortie de l’ampli est un générateur de tension dont l’amplitude vaut la tension d’entrée V_i, multipliée par g, le facteur d’amplification de l’ampli. Ce générateur est représenté par un losange, car c’est un générateur dont l’amplitude dépend de ce qu’il y a en entrée. Je l’ai représenté ainsi par souci de rigueur, mais retenons qu’en sortie, l’amplificateur est un générateur de tension g x V_i relié à une résistance interne de sortie R_OUT.

Eh, mais je connais ce schéma de sortie me direz vous ! Oui, c’est le même que celui du micro guitare vu plus haut, un générateur en série avec une résistance interne.

3 Préambule sur le pont diviseur de tension

Avant d’aller plus loin, je vais vous expliquer ce qu’est un pont diviseur de tension. Nous allons raisonner un moment en régime continu, mais le résultat s’applique aussi en régime alternatif. Considérons la figure suivante :

Circuit utilisé pour expliquer le pont diviseur de tension. — Circuit utilisé pour expliquer le pont diviseur de tension formé par Ra et Rb.

Nous avons une source continue de tension E et 2 résistances R_A et R_B. Aux bornes de R_A la tension vaut U_A et aux bornes de R_B la tension vaut U_B. Un courant continu i circule dans le circuit.

On veut connaître la tension aux bornes de U_A connaissant E, R_A et R_B. Je vous donne vite fait le calcul, il faut utiliser la loi d’Ohm et la loi des mailles. On verrons plus en détails les techniques de résolution de circuit dans un autre article. La compréhension du calcul n’est pas nécessaire, vous pouvez essayer de le suivre ou vous pouvez aller directement au résultat encadré quelques lignes plus bas.

La loi d’Ohm nous dit que :

$U_A=R_A \times i$

La loi des mailles combinée à la loi d’Ohm nous dit que :

$E=U_A+U_B=R_A \times i + R_B \times i = i (R_A + R_B)$

Par conséquent :

$\displaystyle i=\frac{E}{R_A + R_B}$

Finalement, en remplaçant cette expression de i dans l’expression de U_A :

$\boxed{\displaystyle U_A=\frac{R_A}{R_A + R_B}E}$

Que signifie cette expression ? Les résistances R_A et R_B divisent la tension en deux, la valeur de la tension en chacune des résistances dépend de leur valeur, un peu comme une balance qui penche plus d’un côté ou de l’autre en fonction du poids que l’on met sur chacun des deux plateaux. Au plus, on peut avoir E, la valeur de la tension du générateur aux borne d’une résistance, et au moins on aura une tension nulle.

Les personnes qui ont lu cet article ont aussi lu : Comment obtenir un filtre passe-bande avec 2 cellules RC

Regardons les cas extrêmes :

si R_B=0 :

$\displaystyle U_A=\frac{R_A}{R_A + 0}E =\frac{R_A}{R_A}E=E$

Et oui, si R_B=0 on a un fil à la place, et donc toute la tension se retrouve en R_A.

si R_A=0 :

$\displaystyle U_A=\frac{0}{0 + R_B}E =0$

Fastoche, si R_A=0, on mesure la tension aux bornes d’un fil, et la tension aux bornes d’un fil vaut 0 V.

Lorsque ni R_A ni R_B sont nuls, U_A va être compris entre 0 et E.

4. Revenons à nos moutons : requis sur la résistance d’entrée et la résistance de sortie

Maintenant que nous connaissons la formule du pont diviseur de tension, nous allons pouvoir calculer facilement quelle quantité de signal se transfère à l’entrée de l’ampli et en sortie de l’ampli.

4.1 Du micro à l’ampli

Sur la figure suivante j’ai représenté la source (le micro guitare et sa résistance de sortie) et l’entrée de l’ampli (de résistance d’entrée R_IN).

Raccordement du micro de la guitare de résistance interne Rs à l'amplificateur de résistance d'entrée Rin. — Raccordement du micro de la guitare de résistance interne Rs à l’amplificateur de résistance d’entrée Rin.

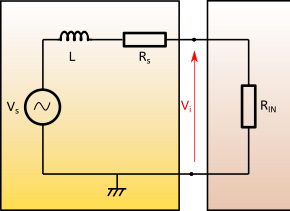
Calculons la tension V_i aux bornes de R_IN en utilisant la formule du diviseur de tension vue plus haut.

Je rappelle que V_s est la tension délivrée par le micro. À l’extérieur, aux bornes du micro on va mesurer une tension V_i inférieure en raison de la chute de potentiel aux bornes de la résistance interne du micro R_s.

On trouve pour V_i :

$\displaystyle V_i=\frac{R_{IN}}{ R_{IN} + R_s}\times V_s$

Nous allons maintenant procéder à un truc que les physiciens aiment bien faire, au grand dam des mathématiciens les plus rigoureux…

Nous allons dire que si R_IN >> R_s (lire R_IN très grand devant R_s), on peut considérer que R_IN + R_s ~ R_IN. A t’on le droit de faire ça ? On fait ça tous les jours non ? 99,99 euros c’est 100 euros non ?

Ce que cela signifie est qu’en faisant de « justes » approximations on va pouvoir tirer des conclusions relevantes. En effet, l’art du physicien réside à savoir ce qui compte et ce qui ne compte pas…

En faisant cette approximation très honnête, on trouve pour V_i :

$\displaystyle V_i=\frac{R_{IN}}{ R_{IN} + R_s}\times V_s \simeq \frac{R_{IN}}{R_{IN}}\times V_s =V_s$

Par conséquent, la résistance interne ne nous dérange pas si la résistance d’entrée de l’ampli est très grande devant elle. Typiquement, on parle au moins d’un facteur 10.

En revanche, si on a R_s >> R_IN, une grande partie de la tension se retrouve sur R_s et donc V_i sera très petit.

Un exemple concret :

Si R_s = 10 ohms, R_IN = 10 kohms et V_s = 3 V :

$\displaystyle V_i=\frac{10000}{ 10000 + 10}\times 3 \simeq 2,997... \simeq 3$

On trouve bien que V_i ~ V_s

En revanche, si R_s = 10 kohms, R_IN = 10 kohms et V_s = 3 V :

$\displaystyle V_i=\frac{10000}{ 10000 + 10000}\times 3 \simeq \frac{3}{2}$

La tension que le micro délivre à l’ampli est la moitié de ce qu’il délivre en interne, car la moitié chute aux bornes de la résistance interne.

Un autre cas extrême, si R_s = 10 kohms, R_IN = 10 ohms et V_s= 3 V :

$\displaystyle V_i=\frac{10}{ 10 + 10000}\times 3 \simeq 0.00099...$

On trouve que si R_s >> R_IN, V_i ~ 0 V.

C’est pour cela que la résistance d’entrée des amplis de guitare est typiquement de 1 Mohms (1 mega ohms =1000000 ohms) car les bobines qui constituent les micro guitare ont une résistance élevée dû au grand nombre de spires. Cette résistance est typiquement de 5-10 kohms.

4.2 En sortie de l’amplificateur

En sortie de l’amplificateur, on a le même schéma : une source qui a amplifié le signal du micro, une résistance de sortie, et une résistance de charge sur laquelle on va brancher l’ampli.

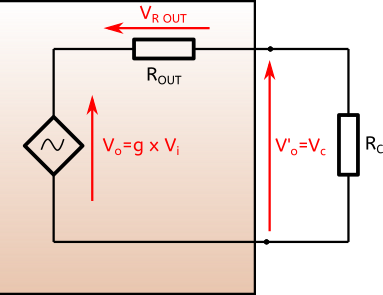
Raccordement de l'amplificateur de résistance de sortie Rout à une résistance de charge Rc. — Raccordement de l’amplificateur de résistance de sortie Rout à une résistance de charge Rc.

Nous avons parlé jusque là d’amplificateur de guitare, mais l’amplificateur représenté ci-dessus peut-être aussi bien une pédale de boost par exemple. Dans ce cas, la résistance de charge sera la résistance d’entrée de la pédale suivante, ou la résistance d’entrée de l’amplificateur de guitare. Dans le cas de l’amplificateur de puissance de l’ampli guitare, alors la résistance de charge sera la résistance du haut parleur.

Adaptation d’impédance en tension

Dans la majorité des cas, en audio, nous cherchons comme précédemment à ce que toute la tension délivrée par l’ampli se retrouve aux bornes de la résistance de charge [1, 2].

Appliquons la formule du pont diviseur de tension pour exprimer la tension V_c aux bornes de la charge :

$\displaystyle V_c=\frac{R_c}{ R_c + R_{OUT}}\times V_o$

Et de même, on va faire une approximation sur les résistances. Si R_c >> R_OUT on a :

$\displaystyle V_c=\frac{R_c}{ R_c + R_{OUT}}\times V_o \simeq \frac{R_c}{ R_c}\times V_o = V_o$

On aura donc une tension maximale aux bornes de la charge si la résistance de sortie de l’ampli est très petite devant la résistance de charge.

Adaptation d’impédance en puissance

Dans certains cas, on cherche à transmettre toute la puissance de la source à la charge au lieu de toute la tension. On parle alors d’adaptation d’impédance en puissance.

Les personnes qui ont lu cet article ont aussi lu : Modélisation d'une diode et simulation SPICE

On peut démontrer que cela est possible lorsque la résistance de charge est égale à la résistance de sortie de l’ampli.

Je vous donne le calcul, il peut sembler un peu compliqué car il fait appel aux dérivées. Vous pouvez passer à la partie suivante si vous voulez.

Nous connaissons la relation entre puissance, courant et tension : P= U x I ou P= U²/ R (voir cet article).

La puissance P_c transférée à la charge est :

$\displaystyle P_c=\frac{{V_c}^2}{R_c}=\frac{ {V_o}^2 R_c }{ ({R_c + R_{OUT}})^2 }$

Jusqu’ici tout va bien. On a l’expression de P_c, la puissance transférée à la charge et en supposant que la résistance de sortie R_OUT est fixe, on veut savoir pour quelle valeur de R_c la puissance transférée est maximale.

Et qui dit maximum dit…?? …Dérivées.

Et oui, on a une fonction, comme une fonction f(x) en maths, sauf que ici f c’est P_c et x c’est R_c. On va donc calculer la dérivée de P_c(R_c), l’annuler et trouver la valeur de R_c correspondante. Tout un programme !

Bon c’est des maths niveau première – terminale S. Si vous n’êtes pas familier avec cela, ne vous inquiétez pas, j’écrirai un article sur les dérivées prochainement.

C’est parti pour le calcul de la dérivée de P_c :

$\displaystyle \frac{dP_c}{dR_{c}}=\frac{V_o^2}{(R_{c}+R_{OUT})^2}+ V_o^2 R_c \frac{-2( R_c+R_{OUT} )}{ (R_c+R_{OUT} )^4}$

= $\displaystyle \frac{V_o^2}{(R_c+R_{OUT})^2}\left(1-\frac{2 R_c}{ R_c+R_{OUT} }\right)$

$\displaystyle = 0$ pour $\displaystyle 1-\frac{2 R_c}{ R_c+R_{OUT} } =0$

soit $\displaystyle R_c+R_{OUT}=2R_c$

donc $\displaystyle R_c=R_{OUT}$

La puissance transférée est donc maximale pour R_c = R_OUT et elle vaut :

$\displaystyle P_{c_{max}}= \frac{V_0^2}{4R_c}$

L’efficacité de transfert $\eta$ est défini comme le quotient entre la puissance transférée à la charge P_c et la puissance dissipée par la source, en l’occurence l’ampli, P_o :

$\displaystyle \eta=\frac{P_c}{P_o}=\frac{V_c \times i}{V_o \times i}= \frac{V_c}{V_o}=\frac{R_c}{R_c+R_{OUT}}$

Dans le cas où R_c=R_OUT, on trouve pour l’efficacité de transfert :

$\displaystyle \eta=\frac{R_c}{R_c+R_{OUT}}= \frac{R_c}{R_c+R_c}=\frac{1}{2}$

Par conséquent, nous venons de démontrer que nous obtiendrons un transfert de puissance maximal lorsque R_c=R_OUT et l’efficacité de transfert est de 50 %.

5 Et l’impédance dans tout cela ?

Dans tout ce qu’on a vu jusque là, on a parlé de résistance. On a certes parlé d’adaptation d’impédance à la fin, mais en utilisant des résistances.

Or la résistance est un composant dont la valeur ne varie pas avec la fréquence du signal.

Cette simplification nous a permis de comprendre que pour que toute la tension de la source se retrouve sur la charge, il faut que la résistance de la charge soit très grande devant la source.

Mais nous ne voyons pas comment évolue la tension de charge avec la fréquence du signal.

Dans un monde idéal, toutes les fréquences produites par la guitare sont amplifiées de manière égale. On a une réponse plane du spectre sur l’ensemble du système audio, des cordes au haut-parleur.

Or dans le monde réel, certaines fréquences sont filtrées.

Pour tenir compte de cela, il faut introduire un concept plus général que la résistance qui est l’impédance. Celle-ci, comme la résistance, exprime l’opposition qu’exerce un composant au passage du courant alternatif sinusoïdal, et sa valeur varie avec la fréquence du signal.

Les condensateurs et les bobines ont un comportement qui varie avec la fréquence, on parlera donc d’impédance.

Dans le cas d’un condensateur, l’impédance diminue lorsque la fréquence augmente.

Et dans le cas d’une bobine, l’impédance augmente lorsque la fréquence augmente.

Notons que dans les deux phrases précédentes j’utilise le mot impédance pour désigner son module, j’espère que vous me pardonnerez cet abus de langage.

Que va t’il se passer au niveau d’un micro de guitare électrique ? Considérons le cas d’un micro à bobine de type simple bobinage (« single coil ») ou double bobinage (« humbucker »). Si on rajoute une bobine dans notre modèle, comme on l’a dit à l’instant l’impédance interne du micro augmente avec la fréquence, et il arrivera inéluctablement un moment où elle ne sera plus suffisamment petite devant l’impédance de la charge qui suit.

Par conséquent, si vous avez bien compris tout ce qui a été dit avant, vous comprendrez que les aigus de la guitare sont filtrés. Ils seront d’autant plus filtrés que l’impédance d’entrée qui suit est petite.

Les détails de cette affaire dans le prochain article…

Vous avez aimé cet article ? Merci de le partager !!

Références

[1] http://hyperphysics.phy-astr.gsu.edu/hbase/Audio/imped.html

[2] https://www.electronicdesign.com/technologies/communications/article/21796367/back-to-basics-impedance-matching-part-1