Dans cet article, comme bien des fois, je vais m’étendre sur une question que m’a posé l’un de vous. Cette question est : peux t’on fabriquer un filtre passe-bande à partir de 2 cellule RC ? En effet, vous savez peut-être qu’en combinant une résistance électrique (R) et un condensateur (C) on peut soit virer des aigus, soit virer des graves. Cela dépendra de comment on agence ces 2 composants. On aura donc dans un cas un filtre RC dit passe-haut, et dans l’autre un filtre RC dit passe-bas.
La question est donc légitime, si en combinant ces 2 types de filtres j’enlève les aigus et les graves, je me retrouve avec le son medium et on doit donc se retrouver là avec un filtre dit passe-bande.
Mais est-ce que ça fonctionne bien ? Si on met des potentiomètres pour faire varier la résistance, est-ce qu’on peut fabriquer un égaliseur pour guitare [1] ?
Et la réponse est : ça dépend de ce que vous voulez 😝. Mais j’y vois surtout là l’occasion de revoir des bases et d’apprendre des choses, donc allons-y, développons !
Sommaire
1 Rappels sur le filtre passe-bas et le filtre passe-haut
Nous avons déjà traité ce genre de circuits, vous pouvez consulter par exemple mon article qui vous explique le filtre RC sans calculs.
Ou vous pouvez aussi continuer la lecture de ce paragraphe !
Un filtre RC c’est tout simple, c’est un circuit qui met en jeu une résistance et un condensateur, et on prend le signal résultant (la tension) entre les 2 composants.
Si on a mis la résistance en 1er, on a un filtre passe-bas, et si on a mis le condensateur en premier, on a un filtre passe-haut.
Voyons ceci en images.
1.1 Filtre passe-bas
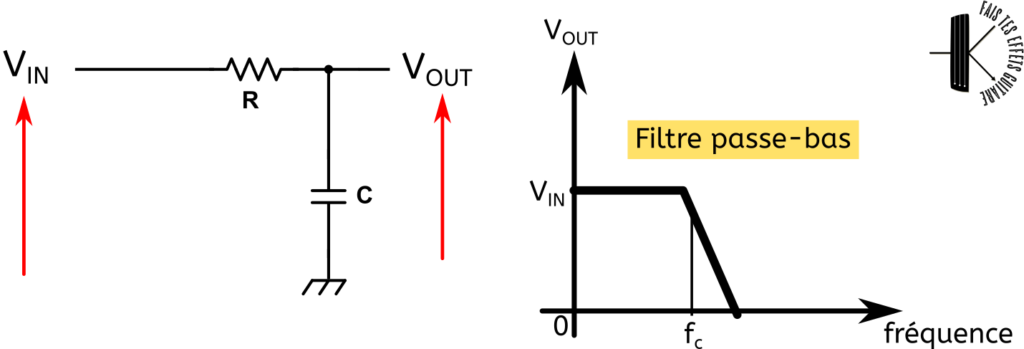
Sur la figure de gauche on voit tout à gauche VIN la tension de notre signal (de guitare ou autre). On relie le signal à une résistance puis à un condensateur qui va à la masse.
En prenant la tension entre ces 2 composants, on va retrouver VIN mais seulement pour les fréquences graves. L’effet de l’association de R et de C est de filtrer les aigus, c’est-à-dire d’annuler la tension des hautes fréquences.
On voit concrètement cela sur la figure de droite où j’ai représenté la tension de sortie du circuit VOUT (son amplitude) en fonction de la fréquence. À basse fréquence, donc dans les graves du spectre audio, on conserve la tension du signal d’entrée. Mais au delà d’une certaine fréquence, la tension de sortie s’annule.
On appelle cette fréquence caractéristique la fréquence de coupure du circuit RC. Sa valeur dépend des valeurs de R et de C :
$$f_c=\frac{1}{2\pi RC}$$
Avec $f_c$ la fréquence de coupure (si le pourquoi de cette formule vous intéresse vous trouverez le calcul ici).
Par exemple si R=10 kohms et C=10 nF, on trouve pour $f_c$ :
$$f_c=\frac{1}{2\pi \times 10.10^3 \times 10.10^{-9}}\simeq 1590 Hz=1,59 kHz$$
Cela signifie que en dessous de 1,59 kHz le signal est conservé, au dessus il est atténué jusqu’à valoir 0.
Notez que j’ai utilisé la notation scientifique pour transformer les kohms et les nF (pour un rappel sur les unités cliquez ici).
1.2 Filtre passe-haut
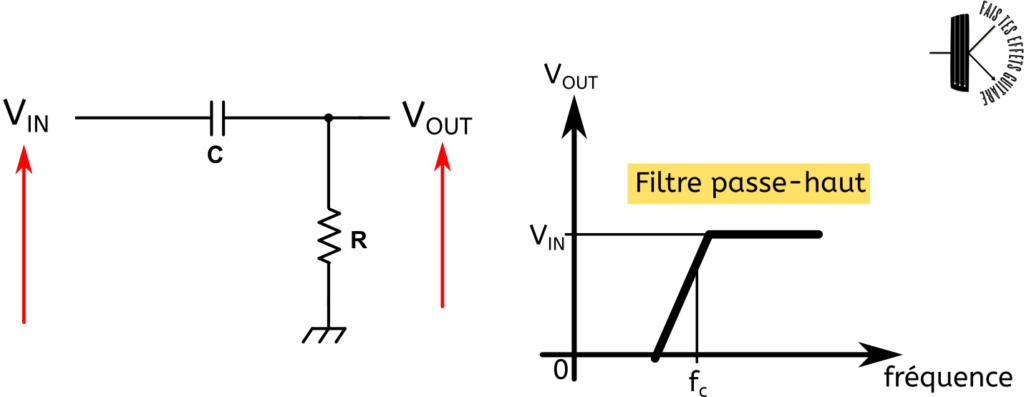
Le filtre passe-haut c’est comme le filtre passe-bas mais on permute R et C comme on peut le voir sur la figure ci-dessus à gauche. On collecte toujours la tension de sortie VOUT au milieu.
À droite, on voit que maintenant ce sont les graves du spectre audio qui sont filtrés et au delà de la fréquence de coupure le signal d’entrée est inchangé soit VOUT=VIN.
2 Filtre passe-bande RC
Que se passe t’il maintenant si l’on monte ces 2 circuits en série ? Est-il possible de filtrer les basses et les aigus ? Un tel circuit peut-il être utilisé pour changer la tonalité de notre son ?
Essayons de répondre à tout cela.
2.1 Circuit du filtre passe-bande RC
Voici le montage que l’on souhaite réaliser :
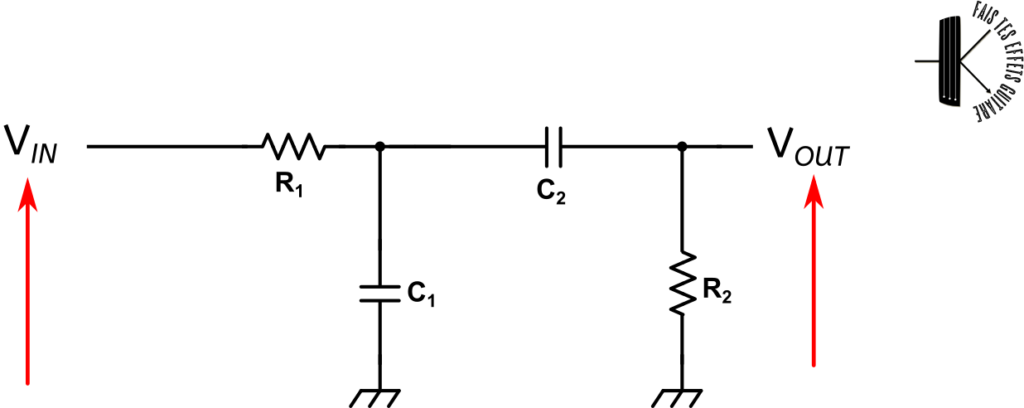
On a donc 2 cellules RC avec R et C permutés pour la 2e cellule. On commence donc par le filtre passe-bas puis on applique le filtre passe-haut.
2.2 Allure de la tension de sortie attendue en fonction de la fréquence
Voici l’allure de l’amplitude de la tension de sortie à laquelle on s’attend, en fonction de la fréquence du signal :
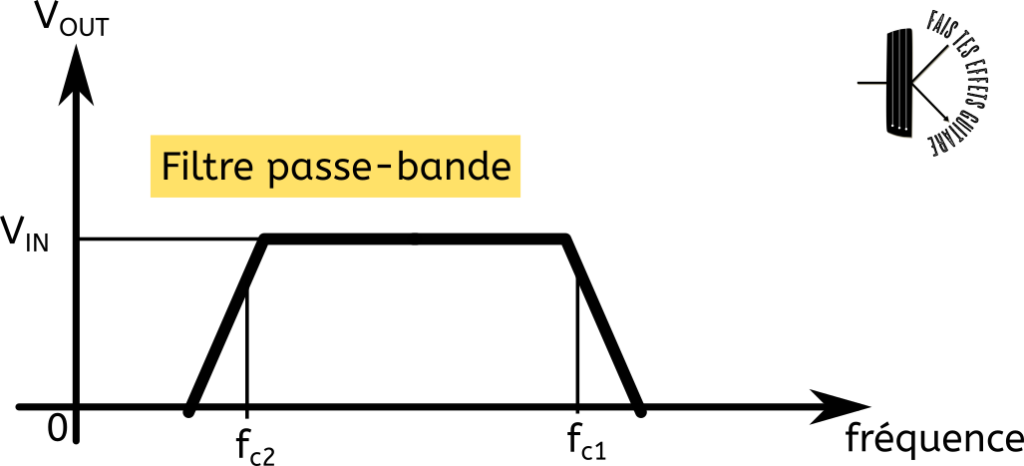
Comme représenté sur la figure ci-dessus, on s’attend à conserver le signal d’entrée, soit VOUT=VIN sur une plage de fréquence comprise entre fc1 et fc2. En dessous et au dessus, la tension de sortie est nulle.
Notez que la fréquence de coupure de la 1ère cellule notée fc1 correspond à un filtre passe-bas et est plus grande que fc2, fréquence de coupure de la 2nde cellule (comme vous l’aurez deviné).
3 Calcul des Fréquences de coupure et Largeur de bande
3.1 Fréquence de coupure
La formule pour la fréquence de coupure est la même que précédemment, sauf que vu qu’on a 2 couples RC, on a 2 fréquences de coupure.
Comme dit plus haut, notons fc1 la fréquence de coupure de la 1ère cellule et fc2 celle de la seconde :
$$f_{c1}=\frac{1}{2\pi R_1C_1}$$
$$f_{c2}=\frac{1}{2\pi R_2C_2}$$
Au passage, on peut également définir la largeur de bande du filtre passe-bande (bandwidth en anglais). Elle correspond à l’intervalle de fréquence pour lequel on conserve notre signal.
En gros, c’est la largeur de notre montagne. Appelons là B:
$$B=f_{c2}-f_{c1}$$
Ça va, celle-là elle était facile ! 😀
3.2 Fonction de transfert et gain du filtre passe-bande RC
Ça par contre c’est un peu plus compliqué. Voici pour ceux que ça intéresse la formule du gain $G$ en fonction de la fréquence $f$, directement :
$$G(f)=\frac{1}{\sqrt{\left(1+\frac{f_{c2}}{f_{c1}}+\frac{R_1}{R_2}\right)^2+\left(\frac{f}{f_{c1}}-\frac{f_{c2}}{f}\right)^2}}$$
Je n’utiliserai pas cette formule ici et je détaillerai dans le prochain article comment je l’ai obtenue.
4 Proposition d’un circuit pratique pour l’audio
Voici ce qu’on veut obtenir concrètement :
- On veut travailler dans le domaine audio donc de 20 Hz à 20 kHz
- On veut pouvoir bouger les fréquences de coupure
Pour le 1er point, il suffit de bien appliquer la formule de la fréquence de coupure.
Pour le 2nd, on doit faire varier soit R, soit C. En pratique, il est plus facile de faire varier R avec un potentiomètre. Voici ce qui devrait se passer si on bouge R2 :
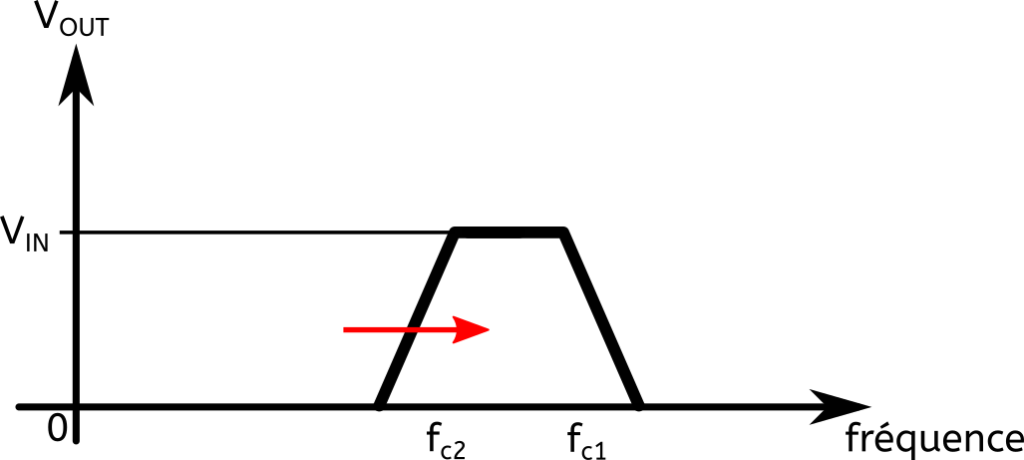
En faisant varier R2 on fait varier la valeur de fc2. Plus concrètement, puisque R2 est au dénominateur dans la formule, en diminuant R2 on augmente fc2. On diminue alors la largeur de bande.
De même en faisant varier R1 on déplace fc1. Si on augmente R1, fc1 se déplace à gauche :

Et si on fait varier simultanément R1 et R2, on aimerait avoir ça :
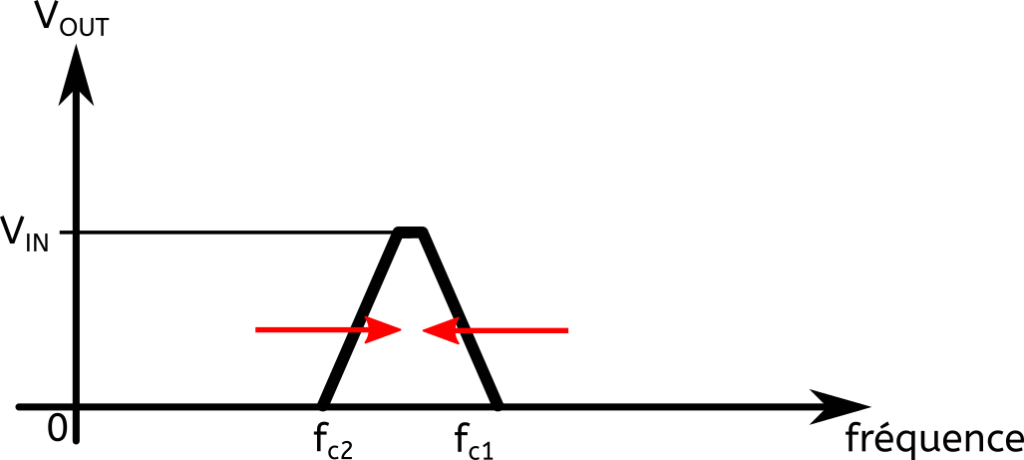
Il faut donc choisir fc1, fc2, puis R1, R2, C1 et C2. Les possibilités sont grandes, il va donc falloir faire des choix.
Ce choix est aussi régit par les valeurs courantes de capacités et de potentiomètre que l’on peut trouver dans les boutiques d’électronique.
Enfin j’ai aussi fait au mieux pour que les courbes montrées dans la partie résultat soient claires (souci de pédagogie quoi !).
J’ai finalement choisi fc1 qui vaut quelques centaines de Hz et fc2 environ 1 kHz. En tenant compte des valeurs disponibles pour R et C j’ai :
- fc2 balaie de 15 Hz à 530 Hz
- fc1 balaie de 1,4 kHz à 48 kHz
On a ainsi un filtre qui au plus large laisse passer de 15 Hz à 48 kHz ce qui s’inscrit bien dans le spectre audible.
Voici comment obtenir les fréquences de coupures, avec les couples :
- C2 = 20 nF et R2 balaie de 15 kohms à 500 kohms
- C1= 2,2 nF et R1 balaie de 1,5 kohms à 50 kohms.
On pourra vérifier que pour fc2 :
| C2=20 nF | |
| R2=15 kohms | fc2=530 Hz |
| R2=500 kohms | fc2=15 Hz |
Et pour fc1 :
| C1=2,2 nF | |
| R1=1,5 kohms | fc1=48 kHz |
| R1=50 kohms | fc1=1,4kHz |
On aura donc besoin d’un potentiomètre de 50 kohms et d’un autre de 500 kohms. Et pour que la valeur minimale de résistance soit de 1,5 kohms ou de 15 kohms, il suffit de leur ajouter une résistance en série (ceci change de manière insignifiante la fréquence de coupure calculée dans les tableaux).
Voici donc suivant tous les arguments présentés jusqu’ici le schéma de circuit que l’on veut étudier :
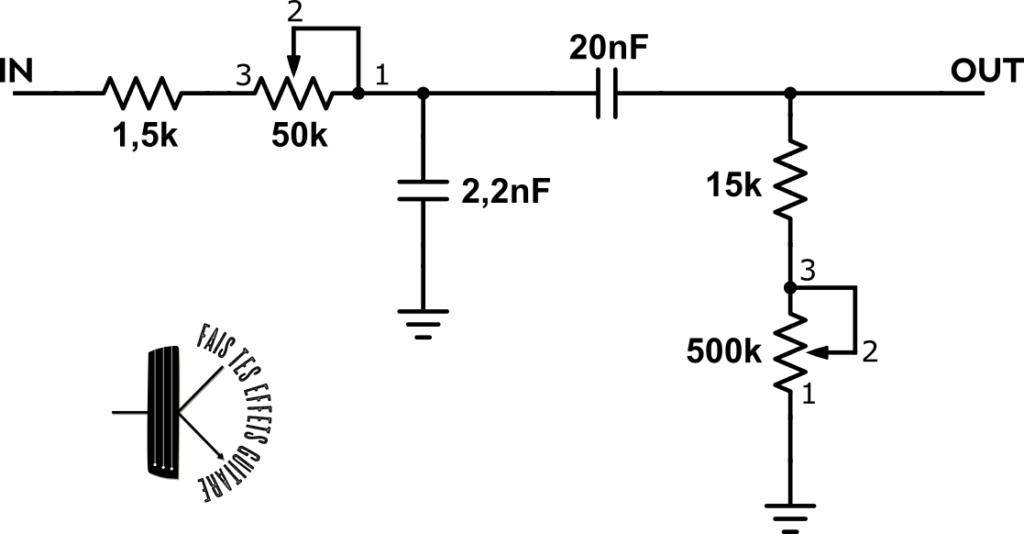
Dans la suite je vais nommer P1 le potentiomètre de la 1ère cellule et P2 le potentiomètre de la seconde.
5 Comportement du filtre passe-bande RC : Simulations
5.1 Faisons varier $f_{c2}$
Regardons la figure suivante, elle nous montre le gain (qui est proportionnel à l’amplitude de la tension de sortie) en fonction de la fréquence. Regardons d’abord la courbe cyan :
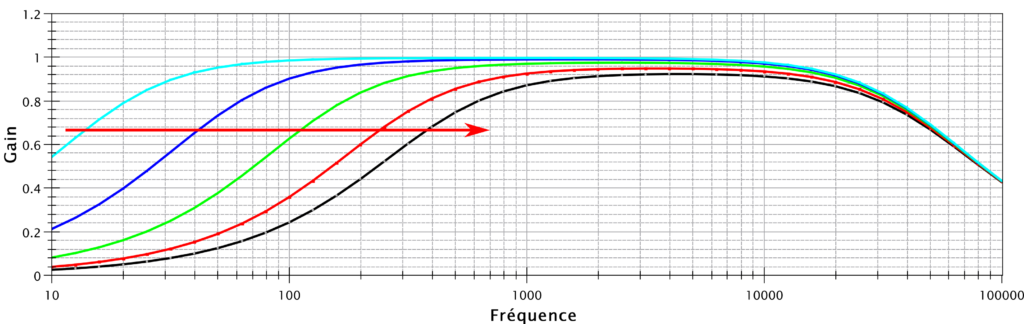
On voit que sur la courbe cyan le gain vaut 1 de 100 Hz à 10 kHz.
En fait, à la fréquence de coupure le gain est un peu plus petit. Il vaut 0,7 (cela correspond aux -3 dB commentés plus haut).
Par conséquent si on regarde les fréquences pour lesquelles le gain vaut 0,7 on trouve 15 Hz à gauche et un peu moins de 50 kHz à droite, ce qui correspond bien à ce qu’on a défini plus haut.
Sur cette même figure, j’ai ensuite fait varier le potentiomètre P2 en allant de 500 kohms à 0. On voit que fc2 se déplace vers la droite car la résistance diminue. On va donc filtrer des basses tout en gardant des aigus.
Top !
5.2 Faisons varier $f_{c1}$
Maintenons fixe fc2 en laissant P2=500k et faisons varier P1 de 0 à 50 kohms :
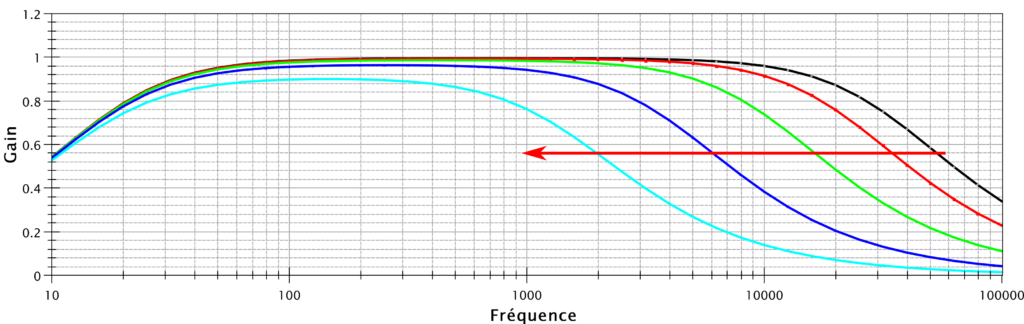
Là c’est pareil, mais on voit qu’on filtre cette fois-ci les aigus tout en conservant les graves du spectre.
Re-top !
Notons toutefois une légère perte de gain lorsque le spectre se rétrécit.
5.3 Plaçons nous au milieu
Cette fois-ci, conservons la courbe cyan de la dernière figure. On a P1=50 kohms et P2=500 kohms.
Nous venons de voir que pour cette valeur de P1 les aigus sont mangés.
Diminuons maintenant la valeur de P2 tout en maintenant P1=50 kohms (je sais ça fait un peu de gymnastique mentale !).
Ceci aura pour effet de filtrer des basses tout en ayant déjà filtré des aigus.
Voyons donc c’que donne la simul’ :
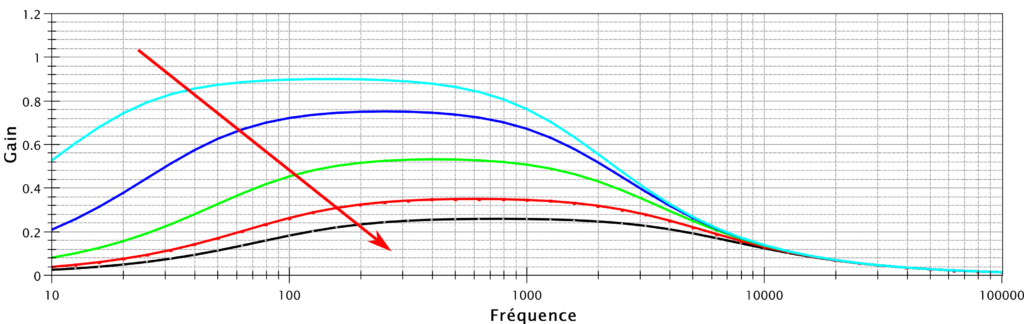
Et oui, là c’est un peu le drame. Certes on voit bien qu’on diminue les graves et donc qu’on fait apparaître une montagne dans les médiums, ce qui est ce qu’on voulait. Mais on voit qu’on perd un facteur 5 sur le gain.
Ça, c’est pas top…
On s’attendait quand même à ça, puisque les 2 filtres se « chevauchent ». Forcement si on filtre tout il ne reste plus rien.
Mais il y a plus que ça en fait…
En fait le problème de ce montage est que la 2e cellule charge la 1ère vu qu’un courant non négligeable s’échappe du 1er vers le 2e circuit. Les 2 cellules ne fonctionnent donc pas de manière indépendante. Ainsi, la réponse de la 1ère cellule va dépendre également de comment la 2e cellule agit dessus.
Le circuit est assez complexe en fait. Pour des fréquences bien éloignées on comprend le comportement du circuit comme étant équivalent à 2 cellules RC indépendantes.
Mais lorsque les fréquences de coupures sont proches, le raisonnement ne tient plus.
On peut cependant simplifier l’appréhension du circuit en considérant le générateur de Thévenin équivalent à la 1ère cellule.
Bon, excusez moi pour le gros mot. Je ne vais de toute façon pas expliquer le théorème de Thévenin ici, mais ce qui en sort est qu’on peut voir la 1ère cellule comme une source de tension qui dépend de la fréquence du signal, en série avec une résistance de source qui est égale à R1 mise en parallèle à C1.
Admettons cela. La conséquence est que dans le présent montage, cette résistance de source fait chuter une bonne partie de la tension du signal. C’est pour cela qu’il ne reste plus beaucoup de tension en sortie. Donc le gain est très faible lorsque les 2 fréquences de coupure sont proches.
6 Amélioration avec un buffer
Cependant, il est possible d’améliorer le circuit. Cela devrait aussi nous éclairer sur la précédente explication.
Regardons ce qu’il se passe si on isole les 2 cellules. On fait cela avec un buffer.
Un buffer, c’est un circuit qui a la propriété d’avoir une impédance d’entrée très grande et une impédance de sortie très faible.
En mettant un buffer à la sortie de la 1ère cellule, aucun courant ne va pouvoir s’échapper car le buffer a une impédance très grande.
Voici à quoi ressemblerait ce circuit, où j’ai inséré un amplificateur opérationnel en configuration suiveur qui a la fonction de buffer :
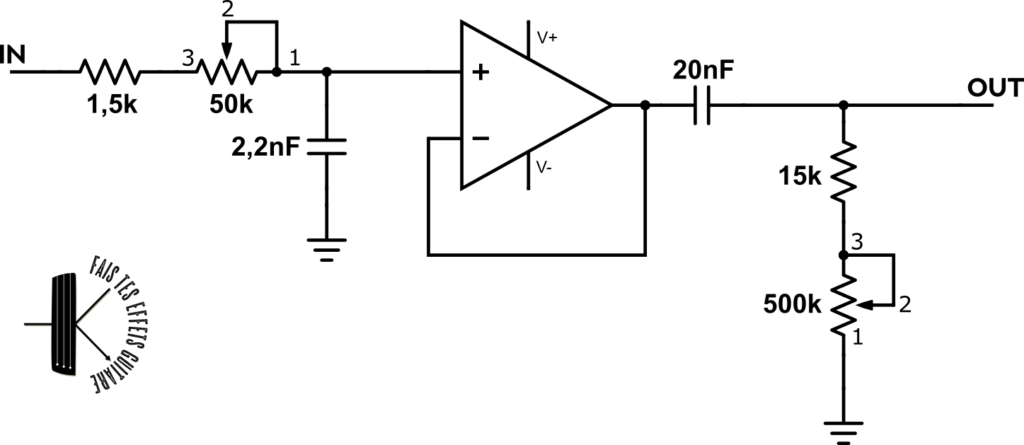
On branche donc la sortie de la 1ère cellule sur l’entrée + de l’amplificateur opérationnel. On boucle l’entrée – avec la sortie pour obtenir un gain de 1 (un buffer n’amplifie pas). Et on branche la sortie de l’amplificateur opérationnel sur l’entrée de la 2e cellule. Les entrées V+ et V- sont les broches pour alimenter l’amplificateur (je n’ai pas représenté les alimentations pour des raisons de clarté).
Voici ce que donne la simulation avec les même paramètres que pour la précédente simulation :
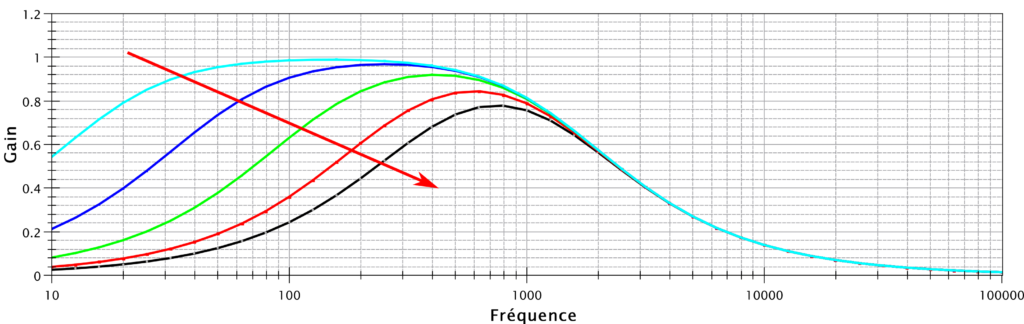
On voit bien le même rétrécissement du spectre, comme on voulait, mais la baisse de gain est beaucoup moins importante (20% contre 50%).
Donc ça c’est mieux !
Par contre le gros désavantage est que le circuit n’est plus passif. Il faut l’alimenter car l’amplificateur opérationnel est un composant actif…
7 Conclusion
Je tiens à remercier ce cher lecteur pour sa question parce que ce genre de questions permet de se creuser les méninges. On a vu que le circuit de base fonctionne si on n’approche pas trop les fréquences de coupure.
On a aussi vu qu’on peut améliorer le circuit en isolant les 2 cellules RC par un buffer. Cependant le filtre devient actif. Ce n’est pas un problème en soit, c’est juste qu’il faut l’alimenter donc c’est un peu une autre histoire.
J’espère que cet article vous a plu. Si vous avez des questions n’hésitez pas à les poser dans les commentaires !!
Références
[1] https://fr.wikipedia.org/wiki/Égaliseur

ok cest cool, mais du coup on a envi de piger le cutoff et la resonance? menfin cest deja super de piger ça! cimer
Bonjour,
je ne crois pas qu’on puisse parler de résonance ici, contrairement à par exemple un circuit RLC série. Celui-ci est aussi passe-bande, mais il montre une réponse maximale pour une fréquence bien déterminée.
Dans le présent cas, c’est juste qu’on atténue à gauche et à droite.
En tout cas merci pour ton intérêt !
Merci Olivier!
Merci ! ☺️
Salut Olivier! Un immense bravo pour cette article, qui répond avec précision et clarté à cette épineuse question !
Merci Pierre ! 😊