
L’autre jour j’ai reçu un courrier de l’un d’entre vous qui me demandait comment fonctionne un filtre RC. C’est-à-dire, on sait qu’en disposant une résistance et un condensateur d’une certaine manière cela va filtrer des aigus ou des graves de notre signal, on connaît la formule, très bien. Mais qu’y a t’il derrière cette formule ? Le but de cet article est donc de voir le problème du filtre RC que j’ai abordé plusieurs fois dans ce blog mais sous un point de vue un peu différent et peut être plus amusant. Je vais adopter un point de vue plus physique et vous expliquer comment fonctionne un filtre RC sans calculs. On ne va pas manier d’équations, mais plutôt des concepts.
Sommaire
1 Exemples d’association R et C
Regardons par exemple la schématique de filtre suivante (qui au passage est le filtre utilisé dans la pédale de distorsion RAT [1]) :
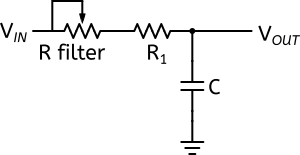
Nous voyons à gauche VIN qui représente la tension d’entrée du circuit et à droite VOUT qui est vous l’avez compris la tension de sortie de ce circuit.
Au milieu, nous avons un potentiomètre monté en résistance variable et une résistance R1 montée en série connectée à la sortie. Nous voyons de plus la présence d’un condensateur qui connecte R1 et la sortie à la masse.
La résistance variable est là pour faire varier la résistance totale, celle-ci étant donnée par Rfilter + R1 (soit la somme des 2 résistances, vous pouvez consulter l’article sur le calcul de résistance équivalente pour plus de détails). Donc grosso modo, on associe une résistance et un condensateur, avec ce dernier qui est connecté à la masse :
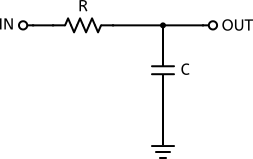
Nous avons vu maintes fois dans ce blog, par exemple dans l’article filtre RC et RAT que cette association résistance et condensateur, soit RC pour faire plus court, forme un filtre.
Rappel sur filtre passe-haut et passe-bas
Ce filtre sera dit passe-bas lorsqu’il laisse passer les graves du signal qu’on lui injecte à gauche, et passe-haut lorsqu’il laisse passer les aigus.
Autrement dit, un filtre passe-bas filtre les aigus, et un filtre passe-haut filtre les graves.
Et on aura un filtre passe-bas dans le cas de la figure ci-dessus, comme illustré ci-dessous :
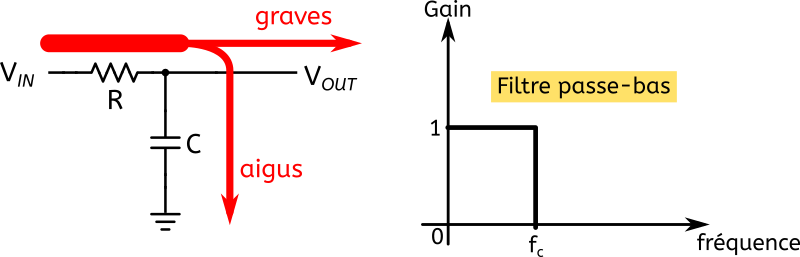
Comment obtenir un filtre passe-haut ? Il suffit d’inverser R et C !
Nous pouvons calculer la fréquence à partir de laquelle le filtre coupe dépend des valeurs de R et de C (vous trouverez le détail du calcul ici). Plus concrètement, on trouve que pour calculer la fréquence dite de coupure que l’on note fc on fait le produit des valeurs de R et de C, on multiplie le tout par 2 π ( avec π=3,14159…). On trouve donc 2 x π x R x C. Puis on prends l’inverse de cette valeur, soit 1/(2πRC).
Considérons un cas un peu plus compliqué
Considérons maintenant le cas d’un amplificateur opérationnel, doté de quelques condensateurs et résistances :
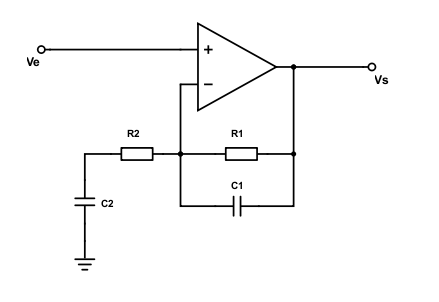
On peut montrer que R1 et C1 forment un filtre passe-bas et R2 et C2 forment un filtre passe-haut. Et on calcule leur fréquence de coupure fc en appliquant la formule vue plus haut, c’est à dire en calculant l’inverse de 2 x π x R x C.
2 D’accord on a la formule, mais comment ça fonctionne ?
En effet, dans le cas de l’amplificateur opérationnel, les résistances et les condensateurs ne sont pas disposés comme dans le cas du filtre RC simple vu au début de cet article.
Par conséquent, on peut se demander pourquoi l’association d’une résistance et d’un condensateur constitue un filtre ??
L’explication « avec les mains » c’est de dire qu’un condensateur c’est comme un interrupteur. Il laisse passer un courant électrique alternatif, c’est-à-dire une variation d’électrons avec le temps. Par contre, si le flux d’electrons est constant, le condensateur bloque ce flux.
Donc en gros, on peut dire que le condensateur est un interrupteur fermé pour un signal à haute fréquence, et un interrupteur ouvert à basse fréquence.
Et ce sont les valeurs de R et de C qui déterminent à partir de quelle fréquence l’interrupteur s’ouvre ou ferme.
La formule nous dit donc combien vaut la fréquence de coupure, mais pas ce qui se cache derrière tout cela. Et pour comprendre la physique qu’il y a derrière tout cela, il faut considérer ce qui se passe dans le temps 😲.
3 Régime transitoire
Considérons tranquillou le circuit suivant :

Il y a une pile, un interrupteur ouvert, une résistance et un condensateur en série. L’interrupteur est ouvert, la pile ne peut donc pas débiter de courant. Il n’y a donc pas de courant électrique dans ce circuit.
Soudainement, fermons l’interrupteur :
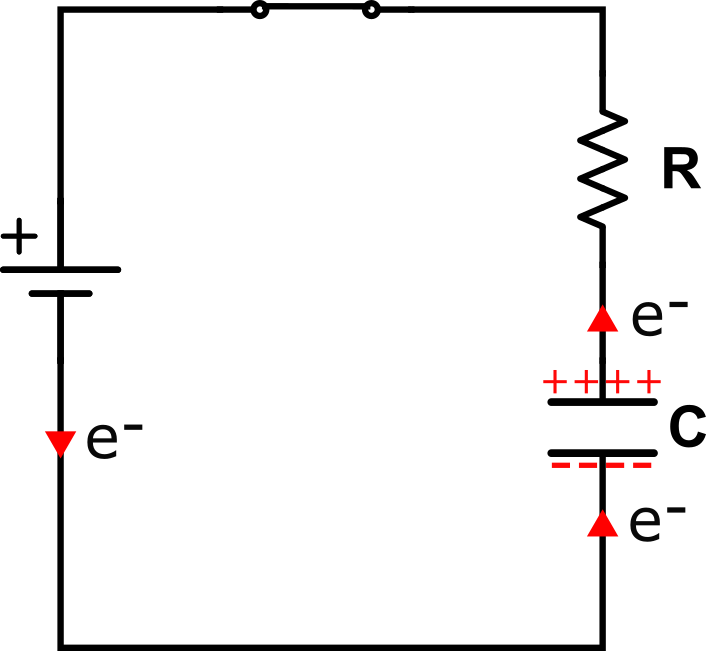
Cette fois-ci, l’interrupteur est fermé. On ferme donc le circuit et un courant d’électrons (donc électrique) doit exister et circuler dans le circuit.
Or, la pile donne un courant constant. Et nous avons vu plus haut que le condensateur bloque les signaux constants, le condensateur devrait donc être équivalent à un interrupteur ouvert ?
Et la réponse est oui, mais après un certain temps.
Regardons le courant en fonction du temps
Pour comprendre cela, imaginons que l’on mesure le courant qui circule dans le circuit en fonction du temps, en prenant pour origine des temps le moment où on ferme l’interrupteur. C’est très facile à faire avec l’instrumentation adéquate et on obtient la figure suivante :
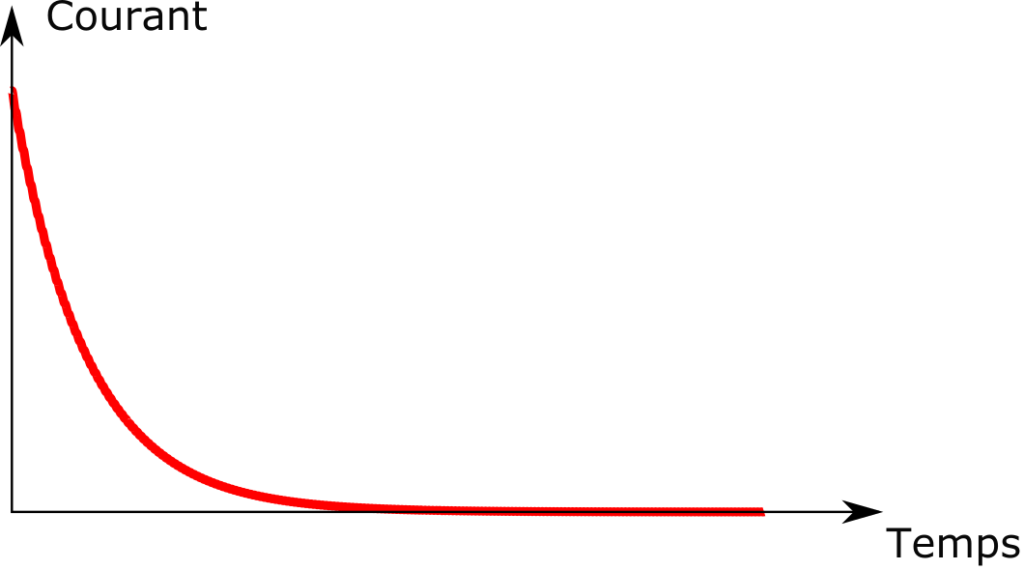
On voit que à t=0, le courant dans le circuit n’est pas nul, il vaut une certaine valeur, puis il décroît avec le temps, jusqu’à valoir 0.
Explication physique
Physiquement, voici ce qu’il se passe. Je rappelle qu’un courant électrique ce n’est ni plus ni moins qu’une circulation d’électrons. S’il y a mouvement d’électrons, il y a un courant électrique. Si les électrons sont bloqués, le courant est nul.
En fermant l’interrupteur du circuit précédant, la pile va débiter des électrons (ils sortent par la borne « moins »). Lorsqu’ils voient le condensateur, ils vont s’accumuler sur les armatures de celui-ci. Vu que les électrons ont une charge négative, j’ai dessiné des « moins » sur l’armature du bas du condensateur.
L’armature supérieure, elle, va libérer des électrons, attirés par la borne positive de la pile. Vu que cette armature aura moins de « moins », elle aura plus de « plus », j’ai donc dessiné des plus sur cette armature (vous me suivez ?).
Par conséquent, durant les premiers instants après avoir fermé l’interrupteur, ont a un mouvement d’électrons qui viennent s’accumuler dans le condensateur, on a donc bien un courant électrique.
Cependant, le condensateur a une place limitée, par conséquent, lorsqu’il n’y a plus de « place » pour les électrons, ceux-ci ne peuvent plus circuler dans le circuit et le courant devient nul.
On constate donc bien que le courant passe d’une certaine valeur à 0 au cours du temps.
Par conséquent, un condensateur bloque un signal continu, oui, après un certain temps (très court en pratique).
Et si on substitue la pile par un générateur de tension alternative ?
Mais que se passe t’il si au lieu d’une pile qui délivre une tension constante on met un générateur de tension alternative, c’est-à-dire dont la tension varie au cours du temps ? 🤔
Disons qu’il délivre par exemple +5V puis -5V, puis +5V et ainsi de suite.
Si le changement de tension se fait rapidement, très rapidement, de manière à ne pas laisser le temps au condensateur de se charger complètement, celui-ci sera successivement en train de se charger et de se charger. Ceci implique qu’il y a toujours mouvement d’électron dans le circuit, donc il y a toujours un courant. De plus, la fréquence de ce courant suit la fréquence du générateur.
Conclusion : le condensateur laisse passer un signal à haute fréquence.
Il nous reste maintenant à comprendre l’influence des valeurs de R et de C dans cette histoire.
4 Temps caractéristique
On a vu qu’une fois l’interrupteur fermé, un courant apparaît et décroit très vite. On veut savoir comment R et C affectent ce temps de décroissance.
Appelons Tau le temps au bout duquel il n’y a plus de courant, c’est-à-dire le temps au bout duquel le condensateur est chargé. Voyons l’effet de R, pour cela, revenons à la figure précédente que je remet ici pour des raisons de commodité :

Nous savons que la résistance s’oppose au passage du courant. Par conséquent, plus R est grand, moins il y aura de courant. Et s’il y a moins de courant, le condensateur aura besoin de plus de temps pour être complètement chargé.
Donc il est censé de supposer que tau est proportionnel à R : plus R est grand, plus tau est grand.
Voyons maintenant l’effet de la capacité C du condensateur. Cette capacité traduit la place disponible pour les électrons. Plus C est grand, plus le condensateur peut contenir des charges. C’est comme dire plus un tiroir est grand, plus il peut contenir de chaussettes.
Par conséquent, si C est grand il faut plus de temps pour « remplir » le condensateur et donc on déduit que tau est également proportionnel à C.
En résumé, on trouve que tau est proportionnel à R et à C, soit tau = k R C, avec k une constante de proportionnalité.
Un instant, cette formule vous rappelle quelque chose …?
La fréquence de coupure…?
Bien vu !
Tau est un temps, fc est une fréquence. Voyons déjà quelle relation il y a entre temps et fréquence.
Relation temps – fréquence
Imaginons que vous attendiez le bus et vous regardez les horaires. Vous avez le temps, vous vous occupez en faisant des calculs, comme tout le monde. Si le bus passe toutes les 20 minutes, il passe 3 fois par heure. S’il passe toutes les 10 minutes il passe 6 fois par heure. Et si maintenant il passe toutes les 5 minutes, il passe 12 fois par heure. On voit donc que plus le temps entre chaque passage est petit, plus la fréquence de passage est grande.
On voit donc que la période de passage (le temps entre chaque passage) et la fréquence sont inversement proportionnels.
Conclusion sur tau et fc
Par conséquent, tau et fc sont inversement proportionnels. Puisque tau = k R C, on retrouve que fc est égal à l’inverse du produit R C !!
Conclusion
En conclusion, un condensateur mets un certain temps à se charger. Le temps de charge est proportionnel au produit R C.
Étant donne que le temps et la fréquence sont inversement proportionnel, on trouve que l’association R C introduit une fréquence de coupure dont la valeur dépend des valeurs de R et de C et qui est inversement proportionnelle au produit R C.
Si la fréquence du signal est plus grande que la fréquence de coupure, le signal passe. Ceci revient à dire si la période du signal est plus petite que le temps caractéristique de charge du condensateur, le signal passe.
Voici donc une explication un peu plus physique et sans équations de comment fonctionne un filtre RC sans calculs. Si le calcul vous intéresse, je ferai ça dans un autre article !
Si vous aimez les articles un peu physique/maths avec les mains sans calculs comme ici dîtes le moi en commentaire en bas de cet article !
Merci d’ailleurs au lecteur qui m’a poussé à écrire cet article et qui certainement reconnaîtra des éléments de nos échanges ici.
Références
[1] https://www.nytimes.com/2012/12/02/magazine/who-made-that-rat-distortion-pedal.html

Bonjour Olivier. C’est tellement agréable de lire tes articles ! On sent la passion pour l’électronique mais aussi la passion de faire comprendre, y compris aux grands débutants et ça ça n’a pas de prix.
Je m’appuie également sur le livre « principe d’électronique » de Albert Paul Malvino et David Bates qui est très intéressant mais qui parfois saute des étapes, comme si ça coulait de sens… heureusement qu’il y a ton site qui me permet de comprendre ce que je n’avais pas compris dans mon livre! (🤫)
Et en plus tu proposes plein de shema faciles à réaliser qui permettent de passer rapidement de la théorie à la pratique et à la magie quand ça fonctionne !
J’ai également découvert Tim Escobedo et son immense travail grâce à toi
Bref tout ça est passionnant, un grand grand merci à toi.
Je mets un commentaire par jour, désolé mais je ne m’attendais pas à découvrir cette mine d’or qu’est ton site après pas mal de déceptions de ne rien comprendre, alors là, ma passion enfouie pour l’électronique et d’arriver à y comprendre quelque chose est complètement débridée 😅
Bonjour Étienne,
oh merci ça me fait vraiment plaisir de te lire. Je suis content de savoir que le site vous aide. Et oui c’est bien de consulter plusieurs sources, de revenir, de persévérer. Personnellement je suis assez lent, j’ai besoin de lire et relire pour que ça rentre 😅. Mais ça fini par rentrer !
N’hésite pas à commenter les articles et à poser des questions, si je peux y répondre c’est avec plaisir.
Bonne continuation ! 😊
Merci ! Enfin quelqu’un qui explique vraiment l’électronique… C’est lumineux.
Ah bah merci ça me fait super plaisir !!!
Excellentes explications. Merci
Merci beaucoup ! 🙂
Je ne ferai pas l’affront de parler de π 😉
Bon… très bon article en tout cas, qui me permet enfin de comprendre physiquement le condensateur en situation de filtrage. Est-ce qu’on peut résumer tout ça en disant que plus on ralenti le remplissage ou plus le truc à remplir est vaste (et à fortiori dans ces deux condition), il y a toujours du mouvement de remplissage-vidage (or mouvement = courant), alors que si au contraire on rempli très vite ou que la boite est très petite, les mouvement de remplissages-vidage durent très peu de temps (par rapport à la période d’oscillation) et donc il n’y a quasiment pas de mouvement (donc de courant), ou en tout cas c’est très bref : faut bien qu’il se charge avant d’être saturée condensateur, quand même, non ?!
J’avoue que sur ce dernier point je bloque un peu :
– je comprends que si la fréquence est très élevée, même avec un courant fort et un capacité faible (le condensateur se rempli rapidement), c’est pas bien grave car on ne rempli jamais le condensateur et le courant ne cesse jamais de circuler.
– je comprends, dans la même configuration, que si la fréquence est basse, le petit condensateur vite chargé sera tout de suite saturé et il n’y aura plus de courant l’essentiel du temps.
MAIS, je bloque sur un point : on parle ici de courant, alors que nous, ce qui nous intéresse, c’est le filtrage des fréquence d’un signal qui varie en tension… (pas en intensité).
Est-ce à dire que la tension disparait quand il n’y a plus de courant, et que donc le signal audio disparait, d’où le filtrage ?
Salut Patrick 😊
Oui je parle de courant car la « manifestation » électrique se traduit par un mouvement d’électrons. Mais courant et tension sont liés. La tension c’est un peu l’équivalent d’une force, capable de bouger des charges électriques, comme le sont les électrons. S’il n’y a pas de tension, il n’y a pas de mouvement d’électrons donc de courant (oui, la lumière peut aussi bouger les électrons mais ce n’est pas de ça qu’on parle). Par conséquent le mouvement des cordes de la guitare entraîne l’apparition d’une tension alternative en sortie du micro qui conduit à un mouvement alternatif d’électrons dans le câble c’est-à-dire un courant. Ces oscillations en tension ou en courant ont la même fréquence (elles peuvent être déphasées mais elles ont la même fréquence, ce qui signifie que le courant suit les variations de tension). Et de même que la corde vibre à différentes fréquences, car il y a des harmoniques, le signal électrique résultant est composé de différentes fréquence. Le rôle du filtre est d’atténuer certaines de ces fréquences (tension ou intensité).
Après on peut aussi résonner en tension. Lorsque le condensateur se charge, il se remplit en charges négatives d’un côté et en charges positives de l’autre. Ceci fait apparaître une différence de potentiel entre les deux armatures (donc une tension), d’autant plus grande que les concentrations en charges sont grandes. Au bout d’un moment, la tension aux bornes du condensateur est égale à la tension de la pile et en sens contraire, ce qui annule la force électromotrice de la pile (celle-ci doit lutter contre une force d’égale intensité).
super je commence a y voir plus clair. merci
Excellent, merci pour votre commentaire ! 🙂
Bonne Vulgarisation ! merci
Bonjour, merci pour votre commentaire, c’est un plaisir pour moi d’expliquer ces choses-là. À bientôt !