3 questions sur l'exponentielle et le logarithme

Je pense que vous aurez déjà entendu parler des fonctions exponentielle et logarithme. Elles sont partout, dans tous les domaines : biologie, physique, chimie, acoustique, électronique, finance, économie, informatique, etc.

Dans la série mathématiques faciles, j’ai décidé d’écrire un court article sur ces deux fonctions. En effet, vous serez amenés à les rencontrer par exemple dans des caractéristiques courant-tension, dans les filtres (diagrammes de Bode), dans la mesure de la puissance acoustique. La définition du décibel par exemple fait intervenir un logarithme. Mais je ne veux pas entrer dans les détails, je veux juste répondre à 3 questions :

Ça ressemble à quoi un logarithme et une exponentielle ?
C’est quoi une échelle logarithmique ?
Ça sert à quoi en pratique ?

Sommaire

Préambule sur les fonctions

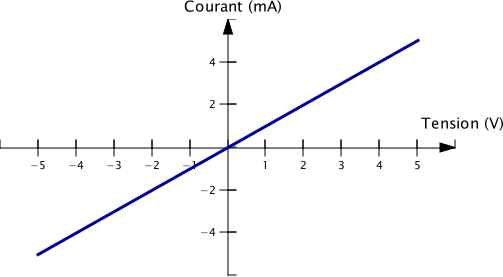
Caractéristique courant tension dans le cas d'une résistance — Un exemple de fonction où le courant est fonction de la tension. Dans le cas présent, on a une droite, ce qui signifie que le courant augmente linéairement, ou proportionellement avec la tension. C’est la loi d’Ohm.

Avant de parler de fonction exponentielle et de fonction logarithme il convient peut-être de définir ce qu’est une fonction. C’est très simple ! Imaginons par exemple que l’on ait une résistance que l’on soumet à une tension. Cette tension entraîne la circulation d’un courant électrique d’une certaine valeur (les concepts de tension, courant et résistance sont expliqués ici). Si l’on applique une autre tension à la résistance, on aura une autre valeur de courant. Le courant dans la résistance dépend donc de la tension, on dit que le courant est une fonction de la tension.

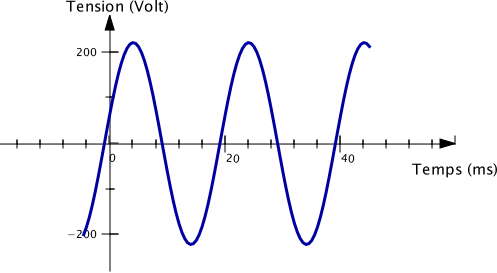
Tension délivrée par le secteur — Autre exemple de fonction : le secteur délivre 220 Volts en alternatif à 50 Hertz, c’est-à-dire que la tension varie de -220 V à + 220 V toutes les 20 millisecondes. La tension dans ce cas est donc fonction du temps.

Un autre exemple : du secteur sort une tension qui varie avec le temps. Si je mesure la tension au temps t1, puis je la mesure au temps t2, je peux trouver une valeur différente. Dans cet exemple, la tension est une fonction du temps.

On peut même préciser que dans le cas de la résistance, le courant varie linéairement avec la tension (une droite sur la courbe I(V)) et dans l’exemple de la tension délivrée par le secteur, la tension est une fonction sinusoïdale du temps, comme l’illustrent les deux figures ci-dessus.

En mathématiques, la fonction ne représente pas une quantité physique, on l’appelle souvent f et la variable x. On note f(x) la fonction f de x. Voyons le cas des fonctions exponentielle et logarithme.

Ça ressemble à quoi un logarithme et une exponentielle?

Soit les trois fonctions f, g, h tel que:

f(x)=exp(x)
g(x)=ln(x)
h(x)=x

où f est la fonction exponentielle, g la fonction logarithme et h une fonction linéaire. On représente ces trois fonctions sur le graphe suivant :

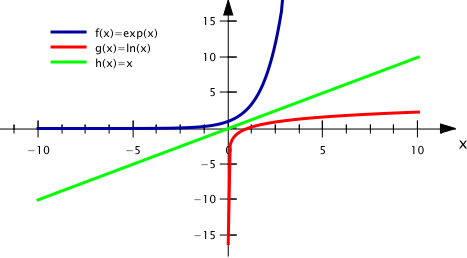
comparaison entre courbes exponentielle et logarithmique — Comparaison de 3 fonctions. En bleu c’est la fonction exponentielle, notée f(x). En rouge on a la fonction logarithme, notée g(x). Ces deux fonctions sont comparées à la fonction identité h(x)=x.

Sur cette figure, on voit que les fonctions f et g sont symétriques par rapport à la fonction h. C’est-à-dire que si on pliait le graphe le long de la droite que fait h(x), f viendrait se coller sur g. Cela signifie que la fonction exponentielle et la fonction logarithme sont des fonctions réciproques. Et ça veut dire quoi réciproque? Pour l’expliquer je vais donner un autre exemple de fonctions réciproques qui sont plus connues : les fonctions carré et racine carrée que l’on note : $x^2$ et $\sqrt{x}$

Comparaison des fonctions carré et racine carrée — Un autre exemple de fonctions réciproques. Les fonctions carré (bleue) et racine carrée (rouge) sont symétriques par rapport à la courbe h(x)=x (verte).

Comme on peut le voir sur cette figure, ces deux fonctions sont symétriques par rapport à la courbe h(x)=x. Ces deux fonctions sont réciproques, car si j’applique une fonction à x puis l’autre fonction, je retrouve x. Ainsi:

Les personnes qui ont lu cet article ont aussi lu : Que sont les dérivées et à quoi servent-elles?

$(\sqrt{x})^2=x$ et $\sqrt{x^2}=x$

Pour le logarithme et l’exponentielle, c’est la même chose. Elle sont par définition réciproques, par conséquent :

$\exp(\ln(x))=x$ et $\ln(\exp(x))=x$

Une note finale avant de passer à la suite, ici on parle de logarithme népérien, c’est pourquoi on le note $\ln$ . Vous aurez peut-être aussi croisé la fonction $\log$ qui s’appelle le logarithme décimal. Les deux sont égaux à une constante multiplicative près : $\ln(x)=\log(x)\times \ln(10)$ et $\ln(10) \approx 2,3$ .

C’est quoi une échelle logarithmique?

1. Échelle Linéaire

Supposons que je mesure une tension, que cette tension varie de 0 V à 10 V, et que je veux dessiner une échelle pour y placer mes mesures. Pour cela je vais tracer un segment, mettre 0 V et 10 V aux extrémités et diviser ce segment en 10 parties égales pour marquer 1 V, 2 V, 3 V, etc.

Maintenant que se passe-t-il si la tension venait à varier beaucoup plus, par exemple on fait quatre mesures et on trouve 0,03 V, puis 1 V, 12 V et 220 V. J’ai représenté ces 4 points sur ce graphe :

Representation en échelle linéaire. On ne voit pas tous les points. — En représentation linéaire, on ne voit pas tous les points.

Vous aurez peut-être aperçu qu’il n’y a que 3 points, or on a fait 4 mesures. Ce n’est pas que j’ai oublié de mettre un point ! C’est juste que sur cette échelle les points 0,03 V et 1 V sont quasiment superposés. On ne peut donc pas se rendre compte de ce qui se passe à basse tension.

Cette échelle est dite linéaire, car s’il y a 2 cm pour représenter 50 V, il y aura 4 cm pour représenter 100 V, 6 cm pour représenter 150 V, etc.

2. Échelle logarithmique

Mais si on avait une échelle où on aurait une puissance de 10 sous chaque division de l’axe, c’est-à-dire 0.01; 0,1 ; 1; 10; 100; 1000, cela nous permettrait de voir de la même manière ce qui se passe à basse tension et à haute tension.

Sur cette figure on voit bien le point à 0,03 V et à 1 V :

Représentation en échelle logarithmique. On voit tous les points. — En échelle logarithmique on voit tous les points.

Et je vous le donne en mille, c’est justement cela une échelle logarithmique!

3. Notion d’ordre de grandeur

Le problème que l’on a ici avec l’échelle linéaire, que l’on a résolu par l’échelle logarithmique, est que les mesures de tension varient sur plusieurs ordres de grandeur. Un ordre de grandeur, on peut le définir ainsi: c’est lorsque l’on passe à une division suivante sur l’échelle logarithmique. De 0,03 à 1 on voit que l’on a passé deux tirets, donc deux ordres de grandeur. De 1 à 12 on a passé un tiret donc un ordre de grandeur. Et de 12 à 220 on a passé un tiret donc un autre ordre de grandeur. Cela revient à dire que l’on change d’ordre de grandeur lorsque l’on change de puissance de 10. Finalement, de 0,03 à 220 on a 4 ordres de grandeur de différence.

Les personnes qui ont lu cet article ont aussi lu : Les nombres complexes : bases

Ça sert à quoi en pratique?

1. Caractéristique courant-tension des diodes

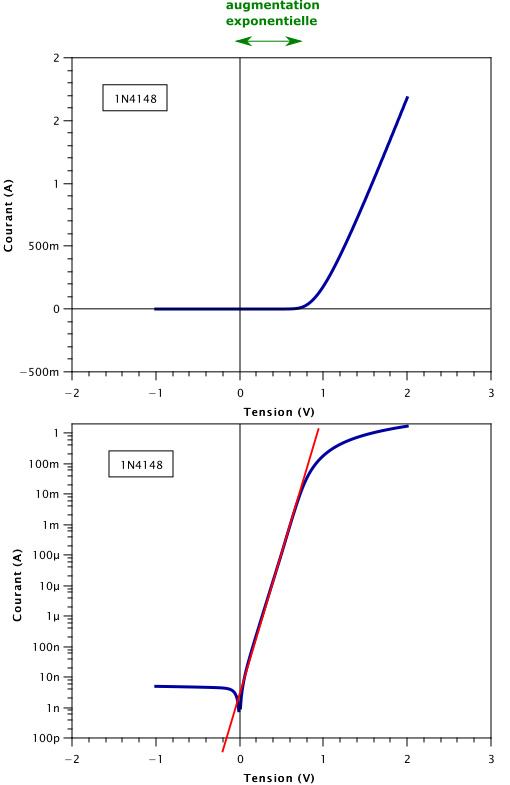
Courbe courant-tension d'une diode. En haut le courant est en échelle linéaire, en bas il est en échelle logarithmique. La ligne rouge est un guide pour les yeux. — Courbe courant-tension d’une diode. En haut le courant est en échelle linéaire, en bas il est en échelle logarithmique. La ligne rouge est un guide pour les yeux.

Comme vous l’aurez peut-être lu dans l’article sur la jonction PN ou celui sur la modélisation de la diode, en polarisation directe le courant d’une diode augmente d’abord exponentiellement avec la tension, puis linéairement. Sur la caractéristique courant-tension, L’utilisation d’un graphe en échelle logarithmique pour le courant va nous permettre de voir cette évolution exponentielle sur plusieurs ordres de grandeurs. Pour cela, je vous ai remis les deux graphes de la simulation d’une diode, au-dessus avec une échelle linéaire du courant et en dessous le même graphe avec une échelle logarithmique pour le courant.

On peut commenter plusieurs choses :

De 0 V à 0,7 V sur le graphe du haut on a l’impression que le courant vaut 0 tout le long. En fait sur le graphe du bas on voit qu’il passe de quelques nA (nanoampère) à quelques dizaines de mA. C’est une variation de 7 ordres de grandeur, c’est énorme !
Toujours de 0 V à 0,7 V on voit sur le graphe du bas que la courbe suit une droite. On déduit donc que lorsque le courant I est en échelle logarithmique, il est proportionnel à la tension V. Ce qui s’écrit mathématiquement :
$\ln(I)\propto V$ (le signe $\propto$ veut dire proportionnel)
$\Rightarrow \exp(\ln(I)) \propto \exp(V)$ (j’ai mis des exponentielles des deux côtés)
$\Rightarrow I \propto \exp(V)$ (on a utilisé le fait que les fonctions logarithme et exponentielle sont réciproque par conséquent $\exp(\ln(I)) =I$ )
Par conséquent, $I \propto \exp(V)$ : le graph du bas nous montre que le courant évolue exponentiellement avec la tension.
Pour les tensions négatives : en haut il semble que le courant soit nul tout du long. En fait il n’en n’est rien, on voit en bas qu’il est très petit mais pas nul et à peu près constant, il vaut quelques nA.

En conclusion on vient de voir un exemple d’évolution exponentielle : dans une diode, le courant augmente exponentiellement avec la tension. En mettant le courant en échelle logarithmique, on fait apparaître les ordres de grandeurs les plus petits.

2. Filtre RC

L’oreille humaine est sensible aux sons allant en moyenne de 20 Hz à 20000 Hz (Hertz). C’est une grande variation puisque cela fait 3 ordres de grandeurs. Lorsque l’on travaillera dans le domaine audio, on devra étudier la réponse des filtres ou des amplificateurs qui composent notre pédale d’effet dans ce domaine de fréquence (20 Hz – 20 kHz).

Vous l’aurez donc deviné, on aura intérêt à utiliser l’échelle logarithmique pour les fréquences !

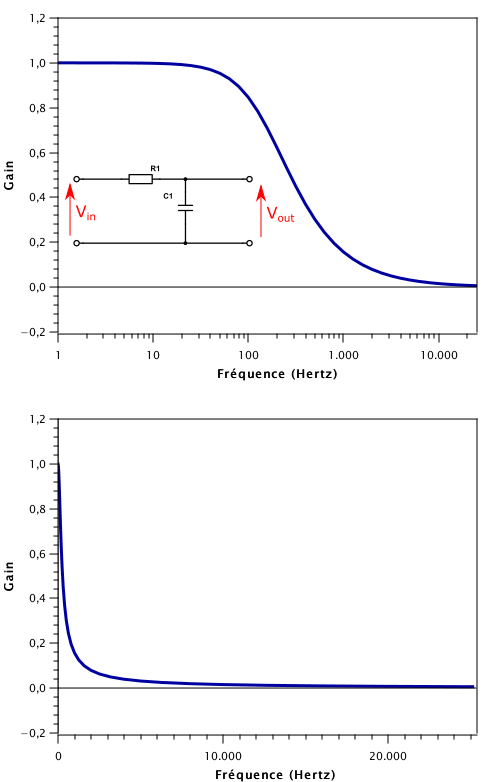
Courbe du gain en fonction de la fréquence pour un circuit passif RC. La courbe du haut a la fréquence en échelle logarithmique, celle du bas l'a en échelle linéaire. — Courbe du gain en fonction de la fréquence pour un circuit passif RC. La courbe du haut a la fréquence en échelle logarithmique, celle du bas l’a en échelle linéaire.

Sur les deux graphes de droite j’ai représenté la réponse en gain d’un filtre passif RC de 1 Hz à 20 kHz (kilohertz, 1 kHz = 1000 Hz). Sous la courbe du haut on voit le circuit en question. Il contient une résistance et un condensateur. Il n’est pas alimenté, c’est pour cela qu’on dit qu’il est passif. Étant passif, ce filtre ne peut pas amplifier, car ce serait fournir une énergie qu’il ne dispose pas. Sa fonction est de laisser passer le son ou de l’atténuer, en fonction de la fréquence de ce son.

Les personnes qui ont lu cet article ont aussi lu : Que sont les dérivées et à quoi servent-elles?

De 1 Hz à 10 Hz, on voit que le gain vaut 1, par conséquent les sons graves passent sans atténuation. En revanche, au-dessus de 1000 Hz, le gain vaut moins de 0,2 ce qui signifie que les fréquences aigües sont fortement atténuées.

Ce filtre est donc ce qu’on appelle un filtre passe-bas, car il ne laisse passer que les fréquences graves.

La courbe du bas est la même courbe, mais avec la fréquence en échelle linéaire. On ne voit pas ce qui se passe pour les basses fréquences. Je l’ai mis juste pour finir de vous convaincre de l’intérêt de l’échelle logarithmique.

3. Potentiomètre logarithmique

Pour finir cet article, je suis allé chercher des infos sur le potentiomètre logarithmique. Celui-ci est présent sur nos guitares ou sur nos pédales d’effet pour contrôler le volume de sortie. En fouillant sur internet je me suis rendu compte de la diversité des opinions qu’il peut y avoir et que personne n’a l’air d’accord sur le sujet ! Je vais tenter de résumer ce que j’ai compris.

Ici je ne parle que de l’aspect technique sur le volume sonore, pas de l’effet du potentiomètre linéaire ou logarithmique sur le son. Car il y a un effet et pour en parler il faut prendre en compte si on utilise un ampli à lampe ou à transistor, sa puissance, si on a une fuzz etc…

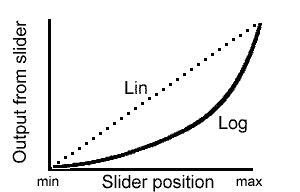
Variation de tension en sortie d'un potentiométre linéaire ou logarithmique. — Variation de tension en sortie d’un potentiomètre linéaire ou logarithmique (http://www.learnabout-electronics.org/Resistors/resistors_09a.php)

Un potentiomètre logarithmique donne une réponse en tension exponentielle (je vous encourage à relire la section sur « Ça ressemble à quoi » 🙂 ). Cela veut dire qu’en début de course, la variation de tension de sortie est faible et en fin de course, la variation est très grande (allure exponentielle).

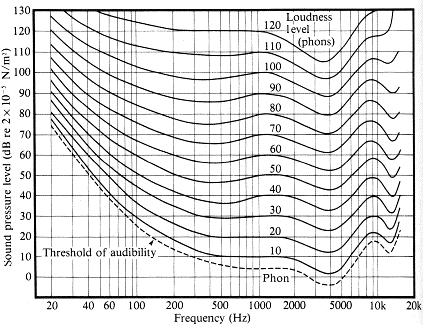
Perception de la puissance sonore par l'oreille — Perception de la puissance sonore par l’oreille (https://electronics.stackexchange.com/questions/101191/why-should-i-use-a-logarithmic-pot-for-audio-applications)

D’autre part, l’oreille humaine perçoit la puissance sonore d’une manière logarithmique. Cela signifie qu’aux faibles puissances sonores, une petite variation de puissance est très notable à l’oreille. Mais aux hautes puissances, il faut augmenter énormément la puissance émise pour sentir une petite augmentation de volume à l’oreille (allure logarithmique).

Le résultat est qu’avec un potentiomètre logarithmique la puissance perçue est plus ou moins linéaire avec la position du curseur du potentiomètre. C’est le résultat recherché.

Si on utilise un potentiomètre lineaire pour le volume, on aura une grande variation de volume en début de course, puis une sensation de volume constant à partir d’un certain point. Ceci n’est pas forcément idéal (au niveau technique !).

Conclusion

Voilà, j’espère que cet article vous aidera à appréhender les mots exponentielle, logarithme et ordres de grandeur.

J’ai essayé de rester simple, et de ne pas aller dans les détails. Si vous avez des questions ou des commentaires, n’hésitez pas à me faire un commentaire au bas de cet article !

Préambule sur les fonctions

Ça ressemble à quoi un logarithme et une exponentielle?