Calcul de résistance équivalente

Des fois, lors d’un confinement par exemple, on veut monter un circuit pour lequel on a besoin d’une valeur de résistance bien concrète. Et il peut se trouver que c’est juste la valeur qu’on n’a pas…!

Cependant, il faut savoir que suivant la fonction de la résistance, utiliser une valeur plus ou moins proche peut fonctionner. Appelons cela la solution triviale.

Mais si on doit mettre exactement cette valeur, on pourra s’approcher au mieux en combinant d’autres valeurs de résistance, à condition de connaître les règles d’association de résistances. C’est le sujet de cet article.

En théorie, on a affaire à deux sortes de groupement de résistances : association en série et association en parallèle. Nous allons voir comment se calcule la résistance équivalente pour chacun de ces groupements, puis nous verrons comment faire le calcul pour un groupement quelconque.

1 Résistances en série

Des résistances sont associées en série lorsqu’elles sont connectées à la queue leu-leu, ou en file indienne comme vous voulez… Regardez par exemple la figure suivante :

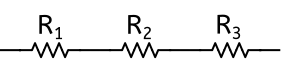
Dans cet exemple, les 3 résistances sont en série. Notez que j’utilise la norme américaine pour dessiner les résistances, car c’est celle que l’on retrouve le plus dans les schéma électroniques de pédales d’effet. En norme européenne, la résistance est représentée par un rectangle.

Voici deux autres cas de résistances associées en série pour le fun :

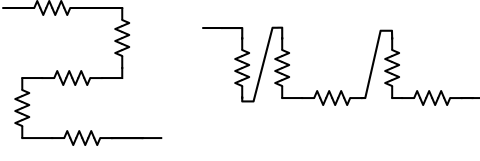
Le calcul de la résistance équivalente est extrêmement simple. Notons $R_{eq}$ cette résistance. On a alors que :

$$R_{eq}=R_1+R_2+R_3$$

C’est une simple somme. Et s’il y a $n$ résistances, on somme les $n$ résistances :

$$R_{eq}=R_1+R_2+…+R_n$$

Regardons un exemple pratique. Par exemple, j’ai besoin d’une résistance de 2k$\Omega$, mais je n’ai que des résistances de 1k$\Omega$. Comment obtenir une résistance de 2k$\Omega$ avec des résistances de 1k$\Omega$ ? Je pense que vous avez compris, en en sommant 2 pardi !

Passons maintenant aux résistances en parallèle.

2 Résistances en parallèle (ou en dérivation)

On dit que des résistances sont groupées en parallèle ou en dérivation lorsque leurs extrémités sont reliées de part et d’autre. C’est le cas par exemple des 3 résistances de la figure suivante :

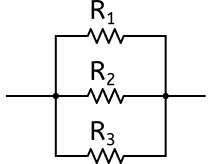
Dans ce cas, le calcul de la résistance équivalente est un peu plus compliqué, il faut calculer des inverses. On trouve en effet que l’inverse de la résistance équivalente est égal à la somme des inverse des résistances qui sont mises en parallèle. Ce qui se traduit mathématiquement ainsi :

$$\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}$$

Et s’il y a $n$ résistances on fait la somme des $n$ inverses :

$$\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+…+\frac{1}{R_n}$$

Vous trouverez une démonstration de cette formule à partir de considérations énergétiques dans la Ref. [1].

Un exemple

Par exemple, si j’ai une résistance de 100 $\Omega$, une de 200 $\Omega$ et une de 300 $\Omega$, la résistance équivalente de ces 3 résistances est :

$\Large \frac{1}{R_{eq}}=\frac{1}{100}+\frac{1}{200}+\frac{1}{300}=\frac{6+3+2}{600}=\frac{11}{600}$

où je me suis arrangé pour mettre toutes les fractions sur le même dénominateur. Ensuite on prend l’inverse pour avoir la résistance équivalente :

$R_{eq}=\frac{600}{11}\simeq 54\Omega$

Sur ce calculateur, vous pouvez vérifier le calcul précédant ou entrer vos propres valeurs :

On remarque que dans un groupement en parallèle, la résistance équivalente est plus faible que la plus faible des valeurs. Dans l’exemple précédant, on voit que la résistance équivalente est de 54$\Omega$, plus petit que la résistance la plus petite qui vaut 100 $\Omega$.

Remarquons également deux choses, la première est que si on a des résistances de même valeurs, la résistance équivalente est une fraction de celle-ci donnée par le nombre de résistances mises en parallèle. En effet, si on a $n$ résistances $R$ :

$$R_{eq}=\frac{R}{n}$$

Par exemple, si je veux 250 $\Omega$ et je n’ai que des résistances de 1 k$\Omega$, je peux mettre 4 résistances de 1k$\Omega$ en parallèle, car $250=\frac{1000}{4}$.

L’autre chose à remarquer, ou plutôt à retenir c’est la formule pour 2 résistances en parallèle. On a :

$\Large \frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}=\frac{R_2}{R_1R_2}+\frac{R_1}{R_2R_1}=\frac{R_1+R_2}{R_1R_2}$

Par conséquent la résistance équivalente de 2 résistances en parallèle est :

$$R_{eq}=\frac{R_1R_2}{R_1+R_2}$$

Vous pouvez tester le calculateur suivant :

3 Résistance équivalente pour un circuit quelconque

Nous pouvons maintenant calculer la résistance équivalente de n’importe quel réseau de résistances, en repérant les résistances qui sont en série et celles qui sont en parallèle.

La marche à suivre est de sommer en 1er lieu les résistances en série, c’est le plus facile à faire. Puis on simplifie le circuit par étapes, en prenant les résistances les plus éloignées de l’entrée et de la sortie du circuit.

Imaginons par exemple le réseau suivant :

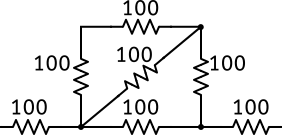
C’est un exemple inventé de toutes pièces, qui n’a pour objectif que d’appliquer ce qui a été dit plus haut. Pour simplifier le problème, j’ai donné la valeur de 100 $\Omega$ à toutes les résistances.

On veut arriver à ça :

Et bien entendu trouver la valeur de la résistance équivalente.

Commençons le calcul…

Revenons au dessin précédant. Nous voyons au milieu 2 résistances en série, je les ai repassées en rouge :

Nous allons commencer par là et les sommer : elles sont équivalentes à une seule résistance de valeur 100 +100 = 200 $\Omega$. Voici le circuit équivalent comprenant cette résistance :

Sur ce dessin j’ai donc remplacé les 2 résistances de 100 $\Omega$ par une résistance de 200 $\Omega$ (en rouge). Nous allons maintenant chercher la résistance équivalente de cette résistance avec celle de 100 $\Omega$ en diagonale. Ces deux résistances font contact à leur extrêmités, elles sont donc en dérivation. On peut donc appliquer la formule des deux résistances en parallèle. La résistance équivalente à ces 2 résistances vaut:

$ \frac{100 \times 200}{100+200} =\frac{200}{3} \Omega\simeq 67 \Omega$

Vous pouvez utiliser le calculateur ci-dessus pour vérifier le calcul si vous le souhaitez.

Nous obtenons donc le circuit équivalent suivant :

On voit la nouvelle résistance de 67 $\Omega$. Elle est en série avec la résistance de $100 \Omega$ que j’ai repassé en rouge (je dis repasser pour faire honneur à l’époque où on pouvait repasser ce qui était écrit sur les slides du rétroprojecteur avec un feutre… 😊).

On va donc sommer ces 2 résistances : on trouve une résistance équivalente de $67+100= 167 \Omega$.

Bon je pense que vous avez compris, je simplifie de nouveau le circuit en remplaçant les 2 résistances par la résistance équivalente :

Cette résistance est en parallèle avec la résistance de 100 $\Omega$. On calcul leur résistance équivalente, elle vaut $\frac{167\times 100}{167+100}\simeq 62 \Omega$

On obtient donc la figure suivante :

Et il ne nous reste plus qu’à sommer ces 3 résistances car elles sont en série. La résistance équivalente totale vaut donc $100 + 62 + 100=262 \Omega$. Voici donc le circuit équivalent au réseau initial :

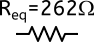
Conclusion du calcul :

Vous n’avez que des résistances de 100 $\Omega$ et vous avez besoin d’une résistance de 262 $\Omega$ ? Utilisez le réseau ci-dessus… ou pas ! Il y a peut être plus simple, comme ajouter 2 résistances en série pour avoir 200 $\Omega$ et un couple de résistances en parallèle pour avoir 50 $\Omega$. On aurait 250 $\Omega$ au total. Il faut aussi dire qu’en pratique, les résistances ont un pourcentage d’erreur sur leur valeur théorique, donc vu que les résistances ne sont pas idéales, on n’aura probablement pas pile-poil 262 $\Omega$ en utilisant le réseau ci-dessus. Tout dépend bien sûr des besoins en précision du circuit que l’on monte.

Si on fait le calcul avec non pas une valeur de 100 $\Omega$ mais qu’on laisse R comme un paramètre, on trouve que la résistance équivalente est de $\frac{21R}{8}\simeq 2,62R$ (je vous invite à le démontrer !). Par conséquent, si je mets des résistances de 200 $\Omega$, j’obtiendrai une résistance équivalente de $2,62\times 200=524 $\Omega$. Bon, c’est un exemple pour illustrer ce que l’on peut faire lorsqu’on connaît les 2 règles de calcul vues plus haut.

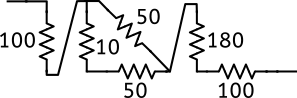
Je vous laisse chercher par vous même la valeur de la résistance équivalente dans le cas du schéma ci-dessous. Dîtes moi la valeur que vous trouvez en commentaires !

Conclusion

Dans cet article nous avons vu les deux configurations possibles pour le groupement de résistances : en série et en parallèle. Nous avons aussi vu comment calculer la résistance équivalente dans chacun des cas, et dans un cas quelconque qui mélange les 2 configurations.

Cet article vous a plu ? N’hésitez pas à le partager !!

Références

[1] https://fr.wikipedia.org/wiki/R%C3%A9sistance_%C3%A9quivalente