Concevoir une pédale boost à ampli op

Rien de tel que de démarquer notre son de guitare lors d’un solo, que ce soit en concert ou en studio ! Pour cela, une pédale de boost permet de monter le volume de la guitare d’un coup au pied. Mais elle permet également de pousser les lampes d’un ampli ou de transformer le son d’une pédale d’overdrive, selon qu’on la positionne avant ou après dans le chaînage des pédales. Dans cet article nous allons voir la conception d’une pédale de guitare boost, à partir d’un amplificateur opérationnel ou ampli op. Tout d’abord, nous verrons le montage amplificateur de base de ce composant. Nous verrons comment l’ajout de condensateurs permet de modifier la réponse en fréquence et concevoir un filtre passe-bande. Enfin je vous montrerai comment transformer le circuit pour pouvoir l’alimenter par une seule pile 9 V.

L’objectif est donc la conception d’une pédale capable d’amplifier les fréquences autour du kilohertz à l’aide d’un amplificateur opérationnel alimenté par une seule pile 9 V.

Sommaire

1 Montage amplificateur non inverseur

Le composant phare de cet article est l’amplificateur opérationnel. C’est un composant très utile en électronique, car non seulement il permet comme son nom l’indique, d’amplifier le son. Mais en l’entourant des composants adéquats, on peut également l’utiliser pour réaliser des opérations mathématiques sur le signal comme l’addition, la soustraction, la dérivation, l’intégration, le filtrage et bien plus. Il y a beaucoup de sites qui répertorient ces différents montages, j’en ai mis quelques-uns dans les références en bas de cet article (voir par exemple [1],[2] et [3]).

Ici je ne vais pas trop faire de théorie. Je vais employer des mots techniques, mais je vais aller directement à ce qui nous intéresse : la conception de notre pédale de boost ! Vous trouverez des articles plus spécifiques sur la théorie de l’ampli op dans ce blog.

1.1 Présentation du montage et gain théorique

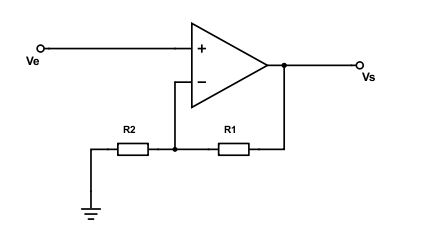
Montage amplificateur non inverseur d'un amplificateur opérationnel. Ve et Vs sont la tension d'entrée et de sortie. R1 et R2 servent à définir le gain du circuit. — Montage amplificateur non inverseur d’un amplificateur opérationnel. Ve et Vs sont la tension d’entrée et de sortie. R1 et R2 servent à définir le gain du circuit.

Nous allons utiliser l’ampli op en montage amplificateur non inverseur. On l’appelle amplificateur car la tension de sortie Vs est plus grande que la tension d’entrée Ve. Cette dernière est le signal qui sort de la guitare. Et « non inverseur » signifie que le signal entre par l’entrée V+ de l’ampli op et non V-.

Les personnes qui ont lu cet article ont aussi lu : Comment mesurer l'inductance d'une bobine ?

Ce montage nécessite deux résistances en plus de l’ampli op, que j’ai notées R1 et R2. Le gain est défini comme ce que l’on reçoit sur ce que l’on donne. Par conséquent le gain $G=$ $\frac{V_s}{V_e}$ . En fonction des valeurs de R1 et R2 que l’on choisit, on aura des valeurs différentes de gain.

Un calcul simple permet de donner l’expression du gain G en fonction des résistances R1 et R2. On trouve simplement que :

$\boxed{\displaystyle G=1+ \frac{R_1}{R_2}}$

1.2 Simultation

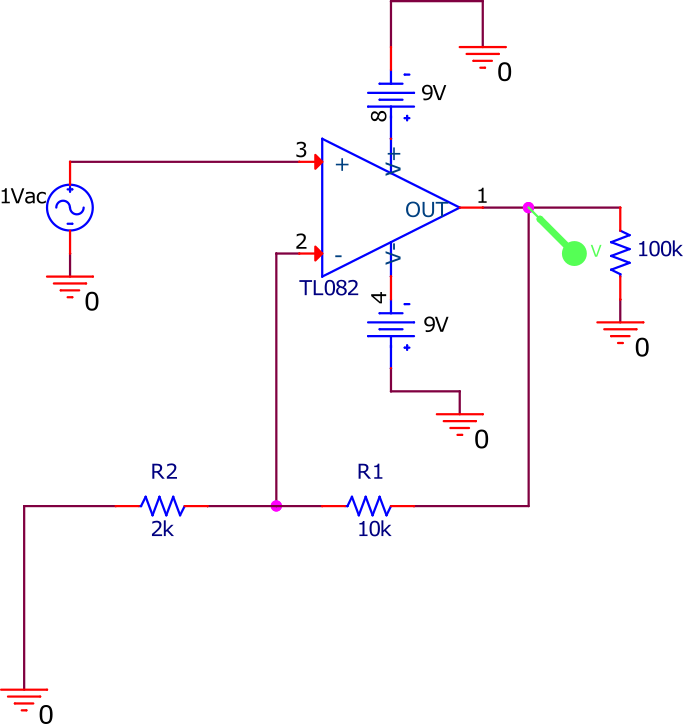
Circuit non inverseur utilisé dans la simulation SPICE. Le générateur de tension sinusoïdal modélise le son de la guitare. Son amplitude est de 1 V et sa fréquence balaye de 10 Hz à 50 kHz.

J’ai simulé avec le programme SPICE ce montage comme point de départ de ce qui suit afin de connaître le gain du circuit en fonction de la fréquence d’entrée. Pour la simulation j’ai choisi les valeurs R1=2k $\Omega$ et R2=10k $\Omega$ . L’ampli op est un TL082, similaire à la série des TL072 très utilisés en audio [4]. J’ai simulé le signal de la guitare par un générateur de tension alternative d’amplitude 1 V. J’ai simulé des fréquences allant de 10 Hz à 50 kHz pour couvrir le spectre de fréquences audibles par l’homme qui va de 20 Hz à 20 kHz. Par ailleurs, ici l’ampli op est alimenté à -9 V et +9 V sur ses entrées -Vcc et +Vcc. En effet, ce composant nécessite en principe une alimentation bipolaire. Dans le graphique suivant on peut voir la valeur du gain G donné par la simulation en fonction de la fréquence :

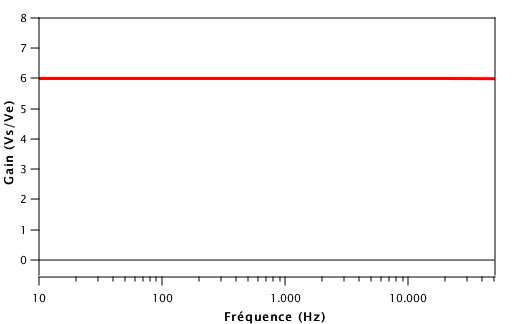
Résultat de la simulation. Le gain du circuit vaut 6 pour toutes les fréquences de la guitare.

On voit ce à quoi on s’attendait : on a un gain constant et ce sur toute la plage de fréquence simulée. Ceci signifie qu’en théorie toutes les fréquences de la guitare seront amplifiées de la même manière. Le gain vaut 6 et se prédit facilement par la formule énoncée antérieurement :

$\displaystyle G=1+ \frac{R_1}{R_2} = 1+ \frac{10000}{2000} =1+5=6$

2 Transformation de la réponse en fréquence

Mais allons plus loin maintenant. Travaillons un peu cette réponse en fréquence. En général, dans un mix, on va couper les fréquences basses et aiguës afin de faire de la place en fréquence pour les autres instruments. De plus, il peut être intéressant d’amplifier les fréquences autour du kHz, car c’est là que la guitare est le plus présente.

2.1 Conception du filtre passe-bande

Nous allons donc continuer la conception de notre booster afin que les fréquences en dessous de 100 Hz et au-dessus de 10 kHz soient filtrées. Cela s’appelle un filtre passe-bande et on veut qu’il ressemble à ça :

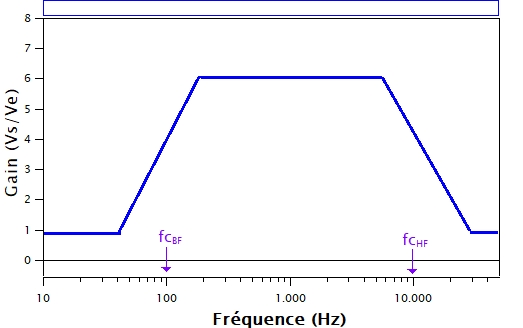
Conception du filtre passe bande à amplificateur opérationnel. On veut que le gain G affecte les fréquences comprises entre 100 Hz et 10 kHz. En dehors, on ne veut pas d'amplification (donc G=1). — Conception du filtre passe-bande à amplificateur opérationnel. On veut que le gain G affecte les fréquences comprises entre 100 Hz et 10 kHz. En dehors, on ne veut pas d’amplification (donc G=1).

Nous allons utiliser le montage amplificateur non inverseur précédant. Mais nous allons y ajouter deux condensateurs, afin de créer l’effet de filtre.

Le montage suivant est typiquement un filtre passe-bande [5]. C’est d’ailleurs si vous y fixez bien à peu de choses près celui que l’on retrouve dans la pédale de distorsion RAT. Je vais expliquer son fonctionnement avec les mains, pour cela il faut d’abord que je rappelle le fonctionnement d’un condensateur avec la fréquence.

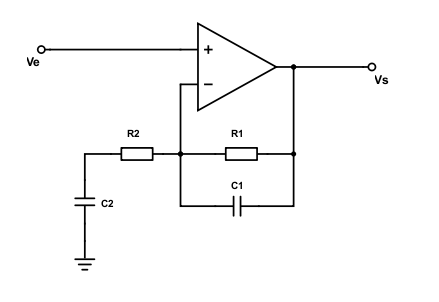
Schéma électrique d'un filtre passe bande à amplificateur opérationnel. La différence avec le premier schéma est le rajout des condensateurs C1 et C2. — Schéma électrique d’un filtre passe-bande à amplificateur opérationnel. La différence avec le premier schéma est le rajout des condensateurs C1 et C2.

2.2 Comportement d’un condensateur aux fréquences extrêmes

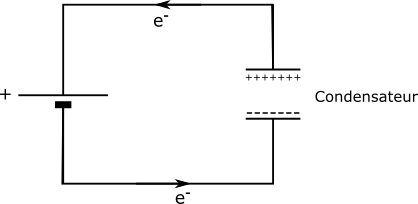
Charge d’un condensateur en régime continu.

Un condensateur est typiquement formé par un isolant entouré de deux plaques de métal (dites « armatures »). Par conséquent, le courant continu ne passe pas puisqu’il y a un isolant. Lorsque l’on polarise un condensateur par une tension continue, il y aura accumulation de charges négatives d’un côté et de charges positives de l’autre (ces charges positives correspondant en fait à un déficit de charges négatives).

Les personnes qui ont lu cet article ont aussi lu : Expérimentation et modifications de la Bazz Fuss

En revanche, en régime alternatif, le condensateur se charge alternativement en charges négatives et positives. Cette alternance se crée des deux côtés du condensateur, par conséquent le courant alternatif « passe ».

On peut donc modéliser le condensateur simplement comme suit :

aux basses fréquences le condensateur est un interrupteur ouvert,
aux hautes fréquences c’est un interrupteur fermé.

La fréquence fc à laquelle on « ouvre » ou « ferme » l’interrupteur dépend de la valeur C du condensateur et de la résistance R qu’on lui associe et vaut :

$\boxed{\displaystyle f_c= \frac{1}{2\pi \times R \times C} }$

2.3 Réponse en fréquence du circuit passe-bande

Appliquons ce petit modèle à notre montage non inverseur doté de ses deux condensateurs. Sur la figure suivante j’ai indiqué les initiales de basse fréquence et haute fréquence sous le schéma équivalent.

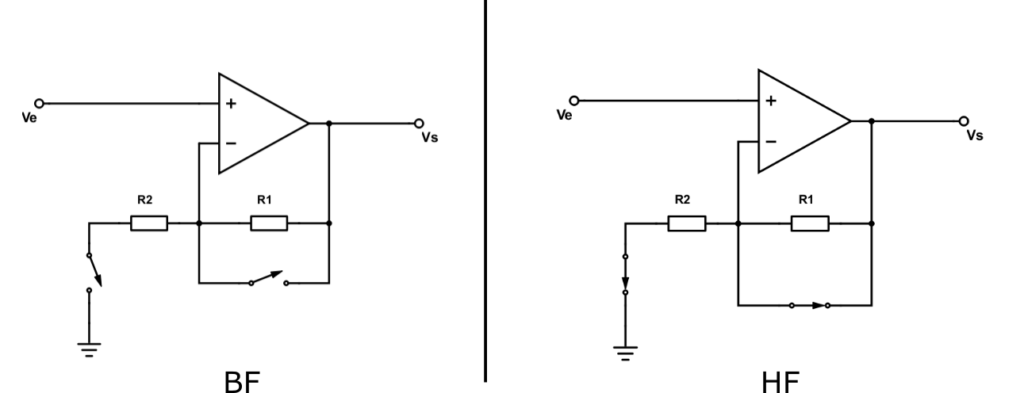
Filtre passe bande modélisé aux fréquences extrêmes. À gauche à base fréquence et à droite à haute fréquence.

En basse fréquence, R1 se retrouve sans condensateur associé, on retrouve donc le cas initial. Par contre, R2 n’est plus relié à la masse. Tout se passe donc comme si on avait un R2 infini. Si on regarde la formule du gain, si R2 est très grand, R1/R2 est très petit. R1/R2 tend donc vers 0 et par conséquent le gain G tend vers 1+0=1.

En haute fréquence, R2 est comme dans le cas initial, sans condensateur. Par contre, R1 est court-circuitée et la résistance de la boucle est donc nulle. Par conséquent le rapport R1/R2 vaut 0 et G=1+0=1.

Nous trouvons donc qu’à basse et à haute fréquence ce type de montage donnera un gain de 1.

Aux fréquences intermédiaires on s’attend à trouver notre cas initial, c’est-à-dire un gain de 6 pour les résistances R1 et R2 que l’on a choisi.

2.4 Calcul de C1 et C2

Nous allons calculer les valeurs de capacité nécessaires pour obtenir une perte de gain en dessous de 100 Hz et au dessus de 10 kHz=10000 Hz. Il faut donc calculer C1 et C2 tel que $f_{c_{BF}}$ =100 Hz et $f_{c_{HF}}$ =10000Hz.

La coupure à haute fréquence est due au couple R1-C1. Si on reprend le calcul de la fréquence de coupure, on a que:

$\displaystyle f_{c_{HF}}= \frac{1}{2\pi \times R1 \times C1}$

On en déduit C1:

$\displaystyle C1= \frac{1}{2\pi \times R1 \times f_{c_{HF}} } = \frac{1}{2\pi \times 10000 \times 10000}$
$\Rightarrow C1=1,59 nF$

De même, on va calculer C2 en sachant que l’on veut une fréquence de coupure $f_{c_{BF}}$ =100 Hz.

$\displaystyle C2= \frac{1}{2\pi \times R2 \times f_{c_{BF}} } = \frac{1}{2\pi \times 2000 \times 100}$
$\Rightarrow C2=796 nF$

2.5 Simulation

Passons maintenant à la simulation. J’ai repris le circuit de simulation précédant en ajoutant juste deux condensateurs avec les valeurs calculées ci-dessus.

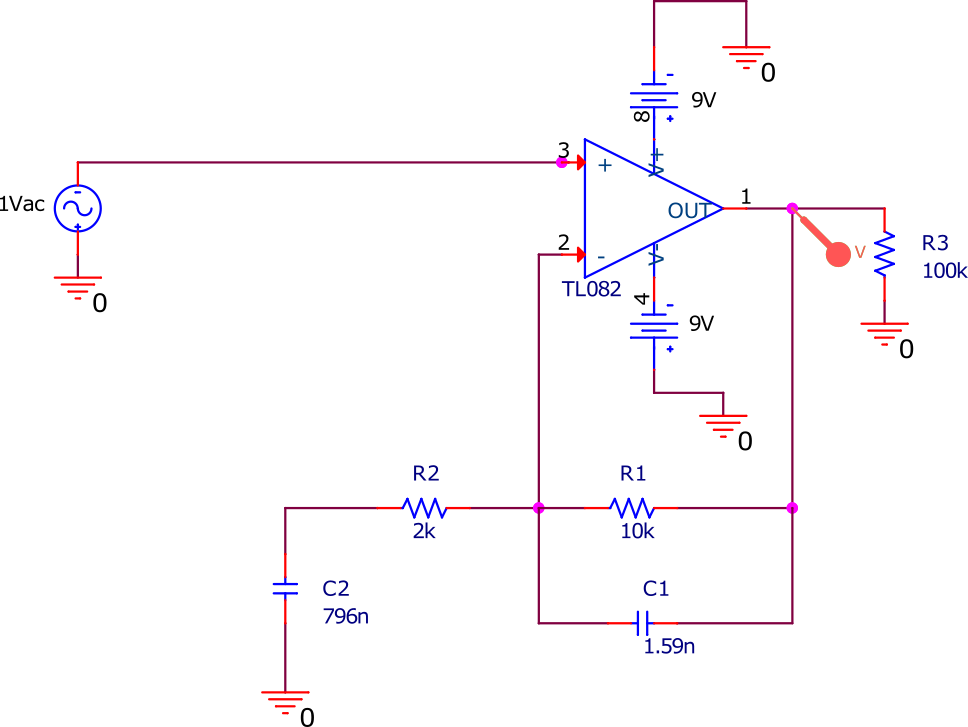
Circuit amplificateur non inverseur passe bande utilisé dans la simulation SPICE. Les conditions de simulations sont les mêmes que précédemment. On a juste ajouté C1 et C2 avec les valeurs calculées dans le texte. — Circuit amplificateur non inverseur passe-bande utilisé dans la simulation SPICE. Les conditions de simulations sont les mêmes que précédemment. On a juste ajouté C1 et C2 avec les valeurs calculées dans le texte.

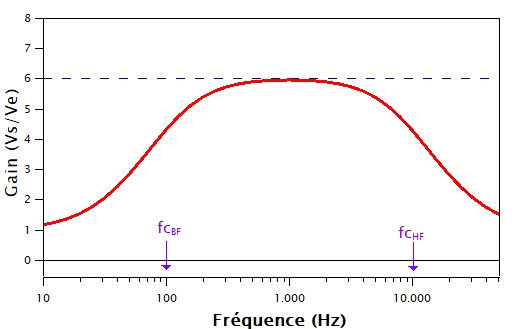
Résultat de la simulation du filtre passe-bande. On trouve les conditions du cahier des charges.

Le résultat de la simulation est donné sur le graphique suivant et ooohhh miracle !!! On trouve la réponse que l’on s’est demandée ! Le gain vaut à peu près 1 à 10 Hz et 50 kHz (il faudrait aller un peu plus loin pour atteindre 1). De plus, entre 100 Hz et 10 kHz on retrouve bien un gain de 6. Finalement, à 100 Hz et à 10 kHz, on trouve un gain de 4,3 ce qui correspond à une baisse de 3 dB (je ne veux pas entrer dans les détails ici, consultez l’article de ce blog sur le diagramme de Bode pour cela !).

Les personnes qui ont lu cet article ont aussi lu : Comment fabriquer une pédale de réverbe - DIY

3 Alimentation mono-tension de l’amplificateur opérationnel

Parfait, on a ce qu’on voulait…

… il reste néanmoins un point gênant, c’est l’alimentation de l’ampli op par deux générateurs ou piles de 9 V… Et nous, en tant que concepteur de pédales pour guitariste nous cherchons à ce que les pédales soient alimentées par une seule pile, si possible. Il y a cependant un moyen d’y parvenir.

Grosso modo l’idée est de monter le potentiel auquel se trouve l’entrée et la sortie de l’ampli op à 4,5 V au lieu de 0 V, c’est-à-dire à la moitié de la tension d’alimentation. On réalise cela en faisant un pont diviseur de tension au niveau de la pile par deux résistances identiques. Et on relie ce point en V+. Le circuit de la simulation est le suivant :

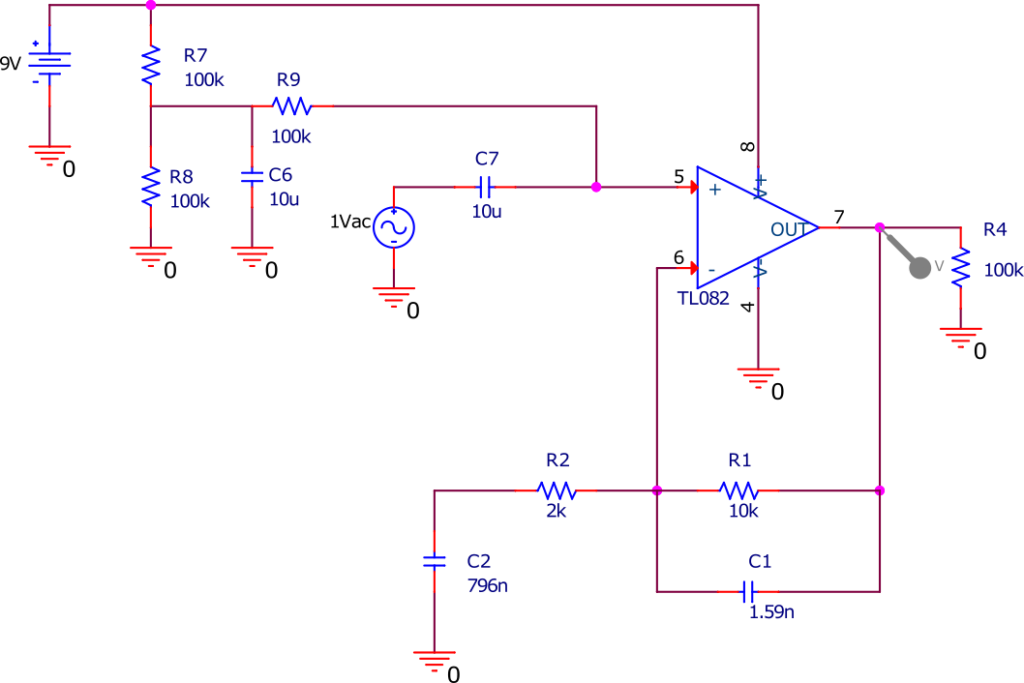
Circuit amplificateur alimenté en mono tension utilisé dans la simulation SPICE. Les conditions de simulations sont les mêmes que précédemment. — Conception finale : circuit amplificateur alimenté en mono-tension utilisé dans la simulation SPICE. Les conditions de simulations sont les mêmes que précédemment.

Le rôle de R9, C6 et C7 est expliqué dans l’article sur l’alimentation mono-tension de l’amplificateur opérationnel de ce blog.

Et là c’est fantastique ! La simulation nous donne la même figure de gain qu’avec l’alimentation en bipolaire (je ne pense donc pas qu’il soit la peine de donner le graphique). La réalisation de notre booster est un succès !

Notez qu’en alimentation mono-tension comme nous venons de le faire il y a tout de même des différences, notamment au niveau de la réserve de modulation (« headroom » en anglais), qui est diminuée. Cela signifie que si la guitare joue très fort, le signal peut saturer.

4 Conclusion

À travers cet article nous avons vu en passant par différentes étapes comment aborder la conception de notre pédale de boost. Il est bien sûr possible de modifier le circuit. En changeant R1, R2, C1 et C2 on jouera sur le gain du circuit et les deux fréquences de coupure. Vous pouvez consulter cet article pour écouter une vidéo de ce circuit et vous faire une idée du son produit.

Si vous avez aimé cet article, n’hésitez pas à le partager ! Merci !!

Références

[1] https://fr.wikipedia.org/wiki/Montages_de_base_de_l%27amplificateur_op%C3%A9rationnel#Amplificateur_non_inverseur

[2] http://electronique.aop.free.fr/liste_aop.html

[3] https://www.electronique-radioamateur.fr/elec/schema/montage-aop.php

[4] https://sites.google.com/site/francisaudio69/6-l-amplificateur/6-8-les-aop-en-audio

[5] http://www.gecif.net/articles/genie_electrique/filtre/

1 Montage amplificateur non inverseur