Modifications de la RAT #2 : la RAT de Ruetz

Après nous être intéressés aux diodes d’écrêtage de la pédale de distorsion RAT, dans cette 2e partie, nous allons nous intéresser à la partie filtrage de l’amplificateur opérationnel et à la modification dite de « Ruetz ». Je rappelle que cet article vient d’un article que j’avais écrit en 2016 sur mon site « artistique » (que vous pouvez consulter ici !). Il est disponible en anglais, mais je le traduis et adapte en français sur le présent blog !

Idée de la modification

J’ai tout d’abord trouvé l’idée de la modification en consultant Wikipédia [1]. Selon eux, le fait de couper la résistance de 47 conduit à une réduction du gain et une augmentation des basses. Il est également possible de faire la même modification, c’est-à-dire ouvrir le circuit au niveau de la résistance de 560 (mais surtout pas les deux en même temps !!). Les deux possibilités conduisent à des basses plus épaisses, dans le genre fuzz, tout en perdant de la distorsion. Sur le site de la RAT de Ruetz [2], ils disent aussi que cette modification est une amélioration énorme comparée à la version d’achat.

Eh ben je vous propose de vérifier tout cela par la théorie avec les mains, par la simulation et par l’expérience !!

1 Description du circuit

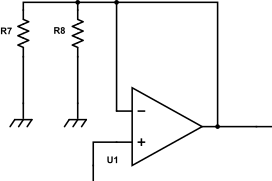
Nous avons déjà parlé de modification de la RAT, en changeant les diodes d’écrêtage. Le schéma électrique est alors le suivant :

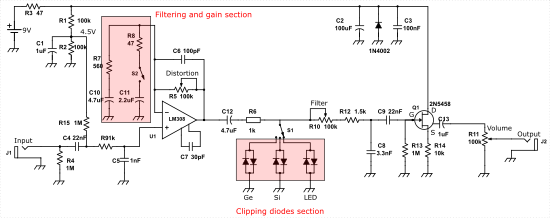
Dans cet article nous allons nous centrer sur le bloc de « filtrage et gain ». Ce bloc, qui contient R7, C10, R8, C11 ainsi que les composants R5 et C6 de la boucle de contre-réaction conditionnent la réponse en gain et en fréquence de l’amplificateur opérationnel.

2 Explication pseudo-théorique de la partie filtrage de la RAT

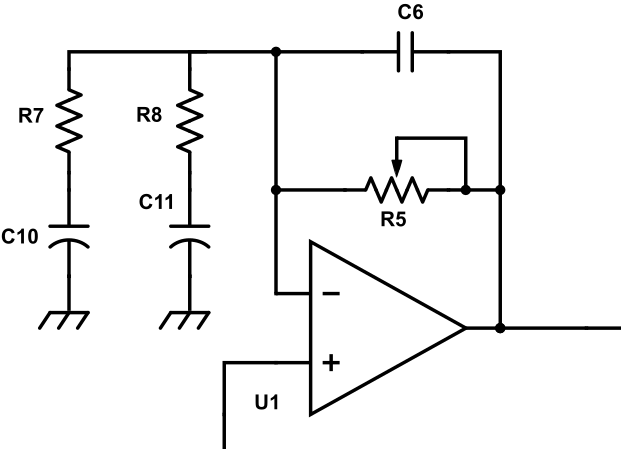
Vous pouvez voir ce bloc sur la figure de droite. Pour expliquer simplement la courbe de gain donnée par ce circuit je vais reprendre l’explication avec les mains que j’ai donnée dans l’article sur la conception d’une pédale de boost à ampli op. En particulier, je vais utiliser la modélisation du condensateur que j’ai faite aux fréquences extrêmes. En effet, le condensateur peut se modéliser par :

• un interrupteur ouvert à basse fréquence
• un interrupteur fermé à haute fréquence

La fréquence de coupure fc (en Hz) où l’on considère que le condensateur change d’état est donnée par :

Avec C la capacité du condensateur en farads (F) et R la résistance qui lui est associée en ohms ().

Nous avions aussi vu que le gain G en tension à la sortie de l’ampli op est défini comme tout gain par la quantité qu’on reçoit sur celle qu’on donne et est donné par l’expression :

Où est la résistance dans la boucle de contre-réaction de l’amplificateur opérationnel, et j’ai appelé la résistance qui va à la masse.

Je vous invite à relire l’article cité ci-dessus pour plus d’explications.

Revenons au schéma de la RAT de la figure 2. Nous avons 3 couples R-C : le couple R7-C10, le R8-C11 et le R5-C6 où R5 est une résistance variable commandée par le potentiomètre « Distorsion ». Nous allons calculer les fréquences de coupure de ces 3 couples :

• R7-C10, on a f1=1/(2 × 560 × 4,7e-6)=60 Hz
• R8-C11, on a f2=1/(2 × 47 × 2,2e-6)=1539 Hz
• R5-C6, on a f3=1/(2 × 10e3 × 100e-12)=159 kHz où j’ai arbitrairement choisit que R5=10k.

J’ai choisi cet ordre de calcul ainsi f1 < f2 < f3. Injectons notre signal de guitare dans l’entrée « + », on suppose que le signal n’a qu’une seule fréquence f. Par exemple si f=440 Hz, c’est la note « la ». Maintenant faisons varier cette fréquence f. Nous aurons 4 cas suivant la position de f par rapport à f1, f2 et f3.

2.1 Analyse en fréquence du circuit

1. Plaçons nous pour f < f1. Nous sommes donc dans le cas où tous les condensateurs sont équivalents à des interrupteurs ouverts.

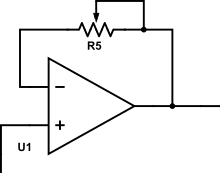
Si on reprend le schéma de la figure 3, on remplace par R5 et vu que l’entrée « – » de l’amplificateur opérationnel n’est plus connectée à la masse, on va remplacer dans l’expression du gain G par une résistance infinie. Si est très grand, est très petit, quasiment nul. Par conséquent le gain G=1+0=1

2. Si f1 < f < f2 : on a que C10 est un interrupteur fermé. Ceci donne le circuit équivalent donné à droite.

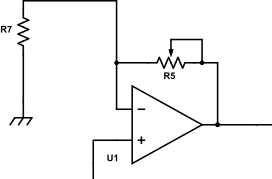
Dans ce cas on remplace par R5 et par R7.

Ceci donne pour le gain :

On trouve donc G=19

3. Dans le cas f2 < f < f3, c’est au tour de C11 de se comporter comme un fil.

R7 et R8 sont en parallèle, on calcule leur résistance équivalente R78 par la formule habituelle :

On trouve alors pour le gain :

Donc ici G=234.

4. Finalement, pour f > f3, c’est au tour de C6 d’être équivalent à un fil. Ceci à pour conséquence que est maintenant nul. On trouve donc que G=1+0=1.

Voilà pour l’étude pseudo-théorique avec les mains ! On trouve que les différentes fréquences du son de notre guitare seront amplifiées de manière différente. C’est entre f2 et f3 que l’on a trouvé la valeur de gain la plus grande, c’est-à-dire au-delà de 1,5 kHz environ.

2.2 Simulation SPICE du circuit

Nous allons maintenant vérifier notre modèle avec une petite simulation SPICE. J’ai entré le circuit suivant dans le simulateur :

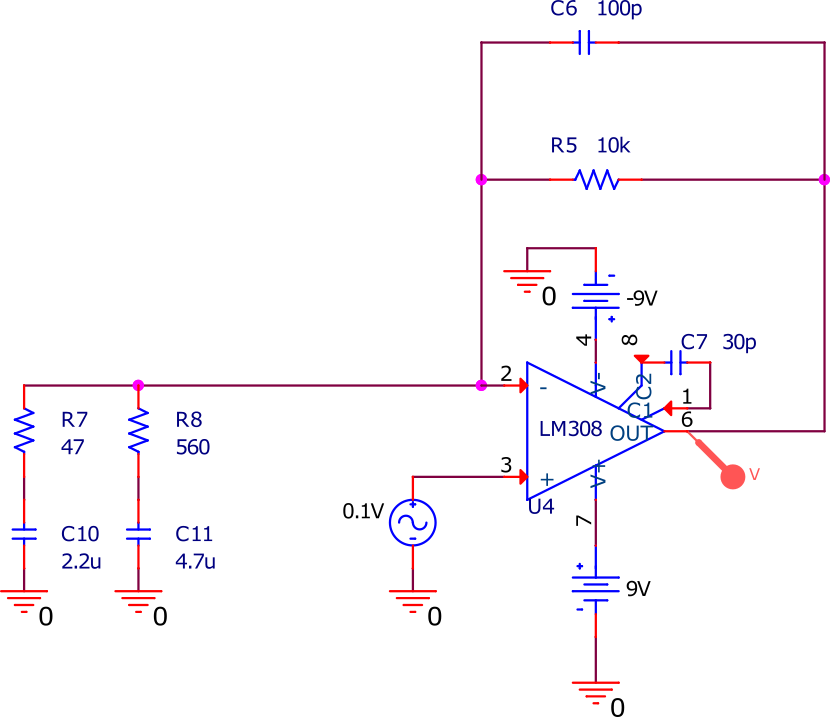
Le signal de la guitare est modélisé par une tension alternative sinusoïdale de 0.1 V d’amplitude. J’ai fait varier sa fréquence de 10 Hz à 1 MHz. Ça couvre largement le spectre audible humain ! En fait c’est pour voir le gain qui revient à 1 à haute fréquence. L’amplificateur opérationnel est le LM308 original.

Le résultat de la simulation donnant le gain en fonction de la fréquence est le suivant :

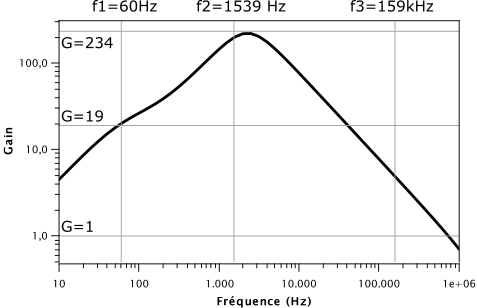
C’est magnifique ! On ne voit pas la valeur du gain G=1 à basse fréquence, il aurait fallu simuler le circuit plus bas, mais ça n’a pas beaucoup de sens physique. On commence donc par un gain proche de 1 à basse fréquence. Le gain augmente et vaut 19 vers 100 Hz. On a vu que c’est dû au couple R7-C10. Puis le gain augmente et vaut 234 vers 10 kHz. Ceci est dû à R8-C11, comme on l’a vu plus haut. Puis le gain chute, en partie en raison du couple R5-C6 de la boucle de contre-réaction. D’autre part, on voit la limitation en fréquence de l’amplificateur opérationnel qui ne permet pas d’amplifier à plus hautes fréquences, car le gain vaut alors moins de 1. Mais cela sera l’objet d’un autre article !

Conclusion : on trouve les même valeurs de gain calculées avec les mains, c’est vraiment chouette je trouve de pouvoir avoir une vision globale de comment fonctionne un circuit sans résoudre aucune équation ! La simulation quant à elle donne une vision plus précise de ce qui se passe.

Je me suis également amusé à faire varier R5 c’est à dire la résistance du potentiomètre de distorsion. On voit apparaître un pic à 1 kHz pour les grandes valeurs de distorsion, ce qui peut rendre le son un peu plus « nasal ».

3 Modification : la RAT de Ruetz

Ayant dit tout cela, nous pouvons maintenant entrer dans le vif du sujet : modifier la RAT originale par la proposition faîte dans la ref [2]. I s’agit ici de modifier le circuit en ouvrant le circuit au niveau de R7 ou de R8 (voir figure 1). Après s’être tapé toute la théorie en haut nous comprenons donc que ceci jouera sur le son en modifiant la forme du gain en fréquence. (Notons toutefois que je ne parle pas d’autres effets comme l’attaque du son, c’est-à-dire l’aspect dynamique du son.)

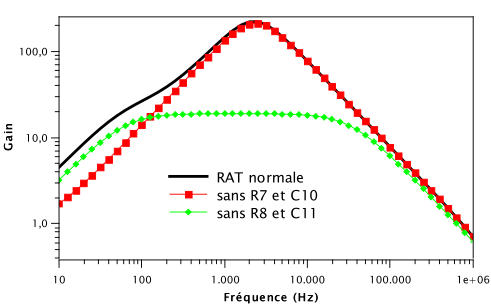
Commençons donc par une petite simulation. J’ai simplement repris le schéma de la figure 8 et j’ai soit enlevé R7 et C10, soit R8 et C11. Le résultat se voit sur le graphique à droite. On voit que si on enlève R7 et C10, cela va jouer essentiellement sur les fréquences basses. J’avais fait l’essai jadis sur mon protoboard et c’est vrai que l’on n’entend guère de différence. Par contre, en enlevant R8 et C11 l’effet est beaucoup plus notable car on perd énormément de médiums aigus et le gain est beaucoup plus faible. Le signal envoyé dans les diodes d’écrêtage est moins grand et on s’attendra à moins de distorsion.

Conclusion : la modification que je fais est d’introduire un interrupteur qui me permet d’ouvrir le circuit au niveau de R8 !

4 Verdict et conclusion

Je finirai cet article par la video que j’avais publiée à l’époque où j’avais écrit cet article. Après coup, je me dis que j’ai un peu trop improvisé, il faudra peut être que je fasse une autre vidéo ! En attendant, on peut quand même apprécier le changement dans le son. Lorsqu’on active la modification, le son devient plus sourd, avec plus de basses, limite plus fuzz. Je trouve cela intéressant dans certains contextes, peut-être plus pour des riff à une notes que des accords bien power. En ce qui concerne le fait que ce soit une modification majeure, je ne trouve pas. La RAT telle quelle sonne plus définie. Par conséquent il est plus intéressant d’ajouter un switch que de couper irréversiblement la résistance R8 selon moi.

Si vous avez aimé cet article n’hésitez pas à le partager ! Merci !!!

Références

[1] https://en.wikipedia.org/wiki/Pro_Co_RAT

[2] https://www.diyguitaramp.com/rat/