Calcul de capacité équivalente

Dans cet article on aborde un aspect basique de l’électronique, mais pas peu utile, le calcul de capacité équivalente. L’idée est de vous donner la formule pour calculer la capacité que l’on obtient lorsque l’on associe deux ou plusieurs condensateurs en série ou en parallèle.

En pratique, ceci s’avère utile lorsqu’on cherche dans nos bacs un condensateur d’une capacité donnée et que c’est justement celle qu’on n’a pas ! Il est donc possible, en associant d’autres valeurs de capacité d’obtenir celle voulue. Il faut juste connaître la formule.

Nous allons d’abord voir la relation entre charge électrique et tension aux bornes du condensateur.

Puis nous aborderons the formule.

Zou.

1 Relation fondamentale

1.1 Charge du condensateur

Nous avons déjà abordé le concept de capacité dans l’article sur les éléments passifs. Je vous en redit quelques mot ici.

Le condensateur est un composant formé de deux plaques métalliques séparées par un isolant (ou diélectrique), qui peut être l’air ou un solide [1].

Le diélectrique a la propriété de ne pas laisser passer le courant continu. Par conséquent, lorsque l’on applique une tension continue à un condensateur, les électrons (particules de l’électricité) qui proviennent du générateur vont s’accumuler sur une des armatures du condensateur. Celui-ci va donc se charger en électrons.

Sur la figure ci-dessus on voit qu’en connectant un condensateur de capacité C à un générateur de tension continue U, une tension U_C va apparaître aux bornes du condensateur.

Pour bien comprendre ce qui se passe, il faut discerner la phase transitoire et la phase stationnaire. Regardons pour cela la figure suivante :

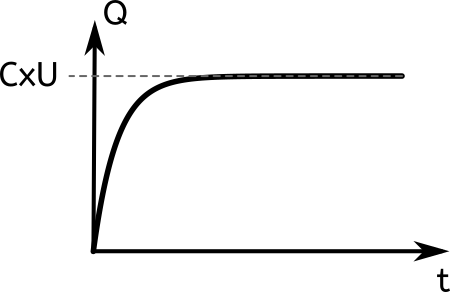
Sur cette figure j’ai représenté la charge totale Q stockée dans le condensateur en fonction du temps. On voit que à t=0, la charge emmagasinée est nulle, puis elle croît jusqu’à atteindre une valeur constante.

Par conséquent, dans le circuit précédant, le courant représenté par la lettre i varie avec le temps. En effet, aux temps initiaux un mouvement de charges est provoqué par le générateur, provoquant l’existence d’un courant électrique qui va s’annuler peu à peu car le condensateur ne pourra plus accumuler plus de charges.

Aux bornes du condensateur, l’accumulation de charges crée une différence de potentiel qui croît avec l’augmentation de la quantité de charge. Une fois le condensateur chargé au maximum, la tension U_C aux bornes des armatures est constante. Dans le présent cas U_C=U.

Une petite parenthèse : si les déplacements de charges sont permis aux temps très courts, on comprends pourquoi le courant alternatif se « propage » à travers le condensateur alors que le courant continu est bloqué.

1.2 Relation fondamentale

La tension U_C qui apparaît aux bornes du condensateur est proportionnelle à la charge qui y est stockée :

$U_C=\frac{1}{C} \times Q$.

Par conséquent, pour une capacité donnée, plus la quantité de charge emmagasinée est grande, plus la tension aux bornes du condensateur est grande.

On écrit généralement la formule du haut ainsi :

$$Q=C\times U_C$$

Si vous revenez au graphique précédant, c’est la valeur indiquée en ordonnée par les pointillés provenant de la courbe. La charge totale atteint donc après un certain temps la valeur C×U_C.

1.3 Précautions d’emploi

La quantité d’électricité correspondant à la charge Q =C×U_C augmente avec U. Quand U_C atteint une certaine valeur, une étincelle jaillit entre les armatures, perce le diélectrique et met le condensateur hors d’usage : on dit que le condensateur est claqué.

La tension U_C doit donc toujours rester inférieure à une valeur donnée, indiquée par le constructeur, et appelée tension de sécurité ou tension de pointe.

2 Calcul de la capacité équivalente

Venons en au fait, comment calculer la capacité équivalente ? Comme pour le calcul de la résistance équivalente, nous allons voir le cas d’association de condensateurs en série et en parallèle.

Commençons par le cas parallèle, car c’est le plus simple !

2.1 Association en parallèle

Supposons que nous ayons 3 condensateurs C₁, C₂ et C₃ montés en parallèle comme dans la figure suivante :

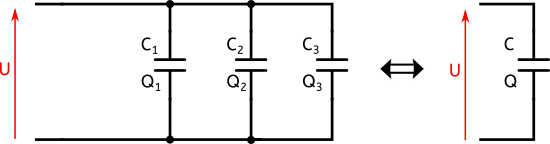
Chaque élément de la figure de gauche est soumis à la même tension U. Et vu que les condensateurs sont montés en parallèle, chaque condensateur est susceptible de recevoir une charge propre Q₁, Q₂ et Q₃. Nous avons donc que :

$Q_1=C_1 \times U$; $Q_2=C_2 \times U$; $Q_3=C_3 \times U$

La charge totale Q du circuit équivalent à droite est la somme des charges emmagasinées :

$Q=Q_1+Q_2+Q_3$

Par conséquent :

$
\begin{array}{l}
Q &=&C_1 \times U + C_2 \times U +C_3 \times U \\
&=& (C_1+C_2+C_3) \times U
\end{array}
$

Or sur le circuit équivalent de droite on a également que :

$Q=C \times U$

Par conséquent :

$Q=C \times U=(C_1+C_2+C_3) \times U$

Soit :

$$C=C_1+C_2+C_3$$

D’où la règle : la capacité équivalente à un ensemble de condensateurs en parallèle est égale à la somme des capacités de ces différents condensateurs.

Par exemple, si j’ai en parallèle un condensateur de 470 nF, 100 nF et 10 nF, la capacité équivalente sera 470 + 100 + 10 = 580 nF.

2.2 Association en série

Considérons maintenant la figure suivante :

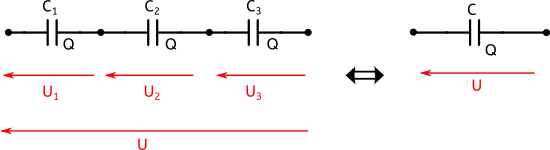
À gauche nous avons 3 condensateurs C₁, C₂ et C₃ montés en série. Contrairement au cas parallèle, chaque condensateur a maintenant à ses bornes une tension propre U₁, U₂ et U₃.

De plus, on trouve également que la charge dans chaque condensateur est la même. En effet, puisque les condensateurs sont branchés en série, le courant qui les traverse est le même ce qui veut dire qu’on a la même accumulation de charges aux bornes de chacun des condensateurs.

Par conséquent la charge mise en jeu est Q.

Nous avons donc d’une part que :

$U=U_1+U_2+U_3$

Et :

$Q=C_1 \times U_1$; $Q=C_2 \times U_2$; $Q=C_3 \times U_3$

Par conséquent :

$U=U_1+U_2+U_3=\frac{Q}{C_1}+\frac{Q}{C_2}+\frac{Q}{C_2}$

Or le circuit équivalent qui nous dit que :

$Q=C\times U$ soit $U=\frac{Q}{C}$

Donc :

$\frac{Q}{C_1}+\frac{Q}{C_2}+\frac{Q}{C_2}=\frac{Q}{C}$

C’est-à-dire :

$$\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}$$

Dans une association de condensateurs en série, l’inverse de la capacité équivalente est égal à la somme des inverses des capacités de chacun des condensateurs.

Par exemple, en montant deux condensateurs de 470 nF en série, la capacité totale est :

$\frac{1}{C} = \frac{1}{470}+\frac{1}{470}=\frac{1}{235}$

Par conséquent C=235 nF soit la moitié.

Voici un petit calculateur en prime !

Enfin, mentionons que rien ne nous interdit de faire un mix entre montage en série et montage en parallèle.

3 Ce qu’il faut retenir

Lorsqu’on associe des condensateurs, le calcul de la capacité équivalente se fait ainsi :

• en série, il faut sommer les inverses des capacités puis prendre l’inverse de ce nombre
  $$\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+…$$

• en parallèle, il suffit juste de sommer les capacités
  $$C=C_1+C_2+C_3+…$$

Vous aurez donc remarqué que c’est comme pour le calcul de résistance équivalente, mais inversé :).

Cet article vous semble utile ? N’hésitez pas à le partager ou à le commenter !!

Références
[1] https://fr.wikipedia.org/wiki/Condensateur