
Dans cet article nous voyons une méthode pour mesurer l’inductance d’une bobine inconnue, sans faire appel à un RLC-mètre [1]. En effet, vous avez peut-être déjà démonté un poste radio et vous avez vu ces composants fait d’un fil de cuivre qui semble faire d’innombrables tours autour d’un cylindre, ou autour de lui même. Ce sont des bobines, qui peuvent avoir plusieurs rôles. On peut les trouver dans les filtres comme les wha wha, ou pour faire une adaptation d’impédance. Ils sont également capables sous forme de transformateur d’augmenter ou de diminuer l’amplitude d’une tension alternative tout en conservant la fréquence.
Ceci va nous permettre de voir ou de réviser les grandes lignes de ce qu’est un circuit résonant RLC. La mesure de l’inductance d’une bobine constituera alors une application pratique de ce savoir.
Si vous voulez réaliser le test en pratique, il faudra quand même vous munir d’un certain matériel, à savoir un générateur de tension alternative (il en existe des modèles pour 60 euros). Dans l’idéal il faudrait aussi un oscilloscope, mais sous certaines limitations que nous commenterons plus bas un multimètre en position tension alternative fera l’affaire.
Sommaire
1 Circuit RLC résonant et détermination de l’inductance
1.1 Qu’est-ce qu’une résonance ?
Faisons l’analogie avec le step (oui, le sport de fitness !). Cette activité vise à « l’amélioration et l’entretien de la condition physique et une évolution du système cardio-vasculaire en provoquant une augmentation de la capacité aérobie (meilleure endurance) » [2]. En gros il faut monter sur une marche puis redescendre.
Penchons nous sur l’effort fourni en fonction de la fréquence à laquelle on exécute le mouvement. À basse fréquence, on monte et on descends trèèèès lentement. On consomme donc très peu d’énergie. Si on augmente la fréquence du mouvement, on va transpirer plus, par conséquent l’effort fourni va augmenter avec la fréquence. Mais jusqu’à un certain point. Notre condition physique nous limite, et au delà d’une certaine fréquence on devrait aller tellement vite que c’est comme si on ne bougeait pas. L’effort fourni diminue donc, et devient nul.
Par conséquent, l’effort fourni en fonction de la fréquence d’exécution du mouvement montre une forme « en cloche ».
Faisons une autre analogie avec une armée qui marche au pas traversant un pont. Si la fréquence du pas est faible, le pont tremblote puis revient à son état initial. Maintenant si la fréquence du pas augmente, le pont tremble plus. Mais si la fréquence du pas est top grande, le pont n’a même plus le temps de trembler. Il reste alors immobile, comme si de rien n’était. Il y a donc une fréquence intermédiaire pour laquelle le pont tremble plus et pourrait même se briser.
C’est aussi un phénomène de résonance : la réaction du système est maximum pour une plage de fréquence intermédiaire.
Et la fréquence pour laquelle le système réagit le plus s’appelle la fréquence de résonance.
1.2 Circuit RLC série
Généralités
Un circuit RLC série est composé d’une résistance de résistance R, d’une bobine d’inductance L et d’un condensateur de capacité C (voir l’article sur les unités). Voici ce circuit :
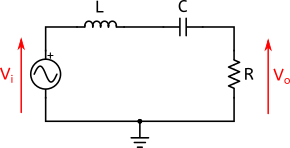
Sur cette figure nous voyons les 3 éléments cités plus haut. Le générateur fournit une tension alternative dont on va faire varier la fréquence. Nous mesurons la tension de sortie aux bornes de la résistance (celle-ci est connectée à la masse).
Comportement avec la fréquence
Regardons ce qui se passe lorsqu’on fait varier la fréquence, en adoptant une approche « avec les mains ». Nous savons que le condensateur bloque le courant continu et que la bobine bloque les hautes fréquences (voir les éléments passifs). On peut donc les comparer à des interrupteurs qui s’ouvrent ou qui se ferment aux fréquences extrême. Suivant ce modèle, aux basses fréquences le « condensateur est ouvert » et la « bobine fermée » et à haute fréquence, le « condensateur est fermé » et la « bobine ouverte ».
Par conséquent, pour le circuit RLC aux fréquences extrêmes on a toujours un « interrupteur » ouvert. À basse fréquence c’est le condensateur et à haute fréquence c’est la bobine. Le courant ne passe donc pas et la tension de sortie Vo est donc nulle.
En revanche, aux fréquences intermédiaires, la bobine et le condensateur laissent passer le courant. Vo n’est donc plus nul. Il y a même une fréquence pour laquelle Vo est maximum.
On observe donc bien un phénomène de résonance dans le circuit RLC, dont voici l’allure :
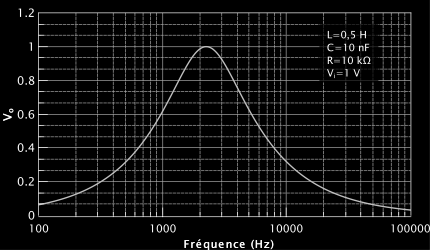
Ce graphe représente l’évolution de Vo en fonction de la fréquence de la tension d’entrée, que j’ai obtenue par simulation. On voit clairement un pic et que Vo tend à s’annuler aux fréquences extrêmes, ce qui confirme bien notre explication « avec les mains ».
1.3 Utilisation du pic de résonance pour déterminer l’inductance d’une bobine
Nous allons utiliser le phénomène de résonance observé plus haut pour déterminer l’inductance d’une bobine.
Pour cela, il nous faut connaître 2 formules, celle qui donne la fréquence de résonance fo, et celle du facteur de qualité Q du circuit qui est liée à la largeur du pic. Plus Q est élevé, plus le pic est étroit et plus il sera facile de déterminer fo et donc L avec précision.
La formule de la fréquence de résonance est la suivante :
$$ f_0=\frac{1}{2\pi \sqrt{LC}}$$
Et voici la formule du facteur de qualité :
$$ Q=\frac{1}{R}\sqrt{\frac{L}{C}}$$
Choix de R
Dans la 1ère formule, nous voyons que R n’intervient pas. Par contre, R intervient dans le facteur de qualité Q. Plus R est grand, plus le facteur de qualité diminue. Voici comment évolue la largeur du pic avec R en théorie :
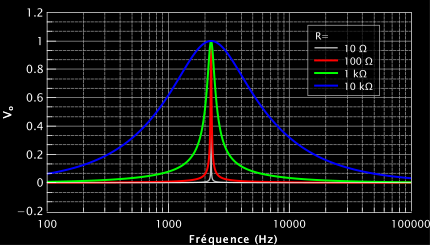
On voit bien que le pic est plus prononcé lorsque R est plus faible. Or il est plus facile de trouver la fréquence du maximum lorsque le pic est étroit que lorsqu’il est large. Par conséquent on a intérêt à choisir R petit pour déterminer fo avec précision.
Par contre, on ne peut pas choisir une valeur trop petite. En effet, tout ce qui est dit jusque là est théorique, mais en pratique il faut tenir en compte le fait que la bobine a une résistance, en raison de sa structure. La bobine est un fil de cuivre et plus la bobine présente de tours de fil de cuivre, plus son inductance augmente mais également sa résistance interne.
Par conséquent, lorsque R sera trop petit, de l’ordre de grandeur de la résistance interne de la bobine, une partie de la tension se perdra dans la bobine. Ainsi si R est trop petite, on ne lira plus rien sur notre appareil de mesure.
La figure suivante illustre ceci. C’est la même simulation que la figure précédente, j’ai juste ajouté la résistance de la bobine en série :
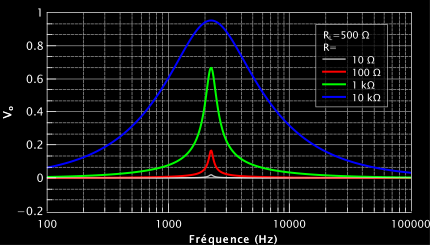
En conclusion, on voit qu’on a intérêt à diminuer R pour la précision en fréquence mais pas trop sinon on perd en précision sur la lecture en volts. Il faudra donc trouver un compromis.
Choix de C
Le choix de C influence la fréquence de résonance ainsi que le facteur de qualité. Et là c’est pareil, il va falloir trouver un compromis. En effet, regardez la formule du facteur de qualité. Vu que C est au dénominateur, en augmentant C son inverse diminue et donc Q diminue. On a donc intérêt à prendre C petit pour que Q soit grand.
Cependant, regardons la formule de la fréquence de résonance. le paramètre C est également au dénominateur. Par conséquent en diminuant la capacité son inverse augmente et donc la fréquence de résonance également. Ceci peut être un problème si notre générateur ne peut atteindre cette valeur ou si notre appareil de mesure ne peut mesurer de tension pour cette valeur de fréquence.
Et oui, le monde de la mesure est exigeant… Blague à part, je trouve que c’est en mesurant qu’on apprends. C’est comme en musique, au final c’est en jouant qu’on apprends. Et si on s’appuie sur la théorie c’est encore mieux !
Dans la partie pratique je vais donner des exemples sur le choix des valeurs de R et de C. Continuons sur l’explication de la méthode.
Mesure de fo et déduction de L
L’idée est donc la suivante, on applique au circuit une tension alternative, d’amplitude 1 V ou plus si nécessaire et on se place à basse fréquence, par exemple à 10 Hz. On mesure la tension au niveau de la résistance à l’aide d’un multimètre ou idéalement d’un oscilloscope. On devrait mesurer peu ou pas de signal.
En augmentant la fréquence, la tension lue va augmenter, passer par un maximum, puis diminuer.
En faisant varier la tension autour du maximum, on va chercher la fréquence pour laquelle la tension est maximale.
Si le maximum présente un plateau trop large, on peut diminuer R pour augmenter le facteur de qualité Q et donc diminuer la largeur du pic.
2 Un exemple pratique
Illustrons cette méthode avec une bobine d’inductance connue. Celle que j’ai a une inductance de 500 mH, que j’ai monté en série avec un condensateur de 47 nF, une résistance de 180 Ω et le générateur de tension alternative.
Pour ceux qui n’ont pas d’oscilloscope, j’ai réalisé l’expérience avec un multimètre digital, que j’ai branché en parallèle de la résistance.

Pour le choix de la résistance, j’ai mesuré la résistance en DC de la bobine, elle vaut 613 Ω. J’ai donc choisi une résistance d’une centaine de ohms (j’en avais une de 180 Ω sous la main). J’ai monté la tension d’entrée à 2,5 V d’amplitude et j’ai commencé à varier la fréquence pour trouver mon maximum. En tâtonnant, j’ai trouvé une fréquence de résonance de 1030 Hz.
Après on peut être plus studieux et faire comme à l’école. Pour bien montrer ce qu’il se passe, j’ai donc récolté quelques points :
| f (Hz) | 600 | 700 | 800 | 900 | 990 | 1000 | 1010 |
| Vo (mV) | 42 | 59 | 87 | 137 | 202 | 207 | 211 |
| f (Hz) | 1020 | 1030 | 1040 | 1050 | 1060 | 1070 | 1100 |
| Vo (mV) | 214 | 215 | 214 | 213 | 209 | 205 | 189 |
| f (Hz) | 1200 | 1300 | 1400 | 1500 | 1600 | 1700 |
| Vo (mV) | 132 | 96 | 74 | 59 | 48 | 41 |
Et je les ai gentiment tracés :
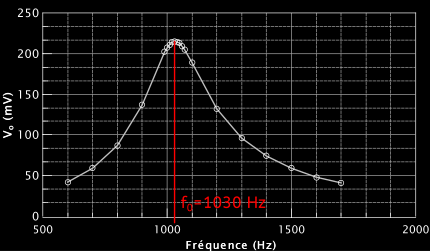
On obtient une belle courbe de résonance, avec une fréquence de résonance fo à 1030 Hz.
On peut alors déterminer L puisque :
$$ f_0=\frac{1}{2\pi \sqrt{LC}}$$
Par conséquent :
$$ L=\frac{1}{4\pi^2 C f_0^2}$$
En entrant les valeurs numériques on trouve que :
$L=\frac{1}{4\times 3,14^2 \times 47.10^{-9} \times 1030^2}=0,508 H=508 mH$
Oh, on est bien proche de notre valeur nominale de 500 mH !!
Petite remarque sur la mesure
Avant d’appliquer la méthode à des bobines inconnues, je voudrais faire une petite remarque sur l’utilisation du multimètre. Celui-ci (en tout cas le mien) n’est pas prévu pour des mesures de tension au delà de 400 Hz selon le manuel. Pour savoir en pratique quelles sont ses limitations, j’ai mesuré la tension aux bornes d’une résistance dans un pont diviseur de tension et j’ai fait varier la fréquence de la tension d’entrée en maintenant l’amplitude constante.
Vu que le circuit ne contient que des résistances, l’amplitude mesurée ne doit pas varier avec la fréquence. Le multimètre retourne un tension constante à basse fréquence, mais j’ai pu remarquer qu’au delà de 1300 Hz, la tension lue diminue. Ceci est clairement dû à une limitation de mon multimètre et signifie qu’avec lui je ne peux pas travailler au delà de 1300 Hz.
Cela limite le champ d’action pour mesurer des bobines de petite valeur. Cependant les bobines d’inductance supérieure à la dizaine de mH devraient pouvoir être mesurées, ce qui peut être suffisant dans le domaine des pédales d’effet.
Ceci signifie également que les 4 mesures à hautes fréquences que j’ai faites sont faussées par mon multimètre. Mais ce n’est pas un gros problème, car ce qu’on cherche c’est la fréquence de résonance qui est inclue dans la zone de « fiabilité » de mon multimètre.
Cliquez sur le bouton pour charger le contenu de docs.google.com.
3 Mesure de l’inductance de bobines inconnues
Les composants présentés ici proviennent d’une petite radio d’un certain âge.
J’utiliserai ce calculateur d’inductance pour obtenir rapidement mes valeurs de L à partir des valeurs de la capacité C utilisée et de la valeur de f0 mesurée.
J’ai fait les mesures avec mon oscilloscope, vu les grandes valeurs de fréquences de résonance atteintes parfois.
Commençons par ce petit transformateur :

Ce transformateur est composé de 2 bobines indépendantes, une pour le primaire et l’autre pour le secondaire. Mesurons l’inductance de la bobine du primaire.
Pour cela j’ai pris C=1 nF, R=15 Ω et j’ai trouvé f0=50 kHz. Je déduis L=10,1 mH.
Pour le transformateur noir de la photo de tête de cet article, avec le même condensateur j’ai trouvé f0=3800 Hz, ce qui me donne L=1,75 H. Ça c’est intéressant pour me fabriquer une wha-wha ou un filtre passe bande !!
Examinons cette petite bobine :

En prenant C=470 nF, R=15 Ω, je trouve f0=31 kHz soit L=56 uH. Pas bézef mais instructif !
Finissons par cette autre petite bobine :

J’ai pris C=1 nF, R=4 Ω, je trouve f0=1,86 MHz soit L=7,32 uH. Bon je m’attendais à plus. Ça à l’air d’un petit transformateur, peut-être que je lui trouverai une application !
Voilà pour quelques exemples. La difficulté réside dans les choix de R et C, dont j’ai mentionné les critères de sélection plus haut. Mais avec un peu de patience et de réflexion on y arrive.
Pour aller plus loin, dans le cas où on nécessite une valeur très précise pour une application bien concrète, il faudrait entrer dans le calcul des incertitudes. Le condensateur par exemple a une tolérance que donne le fabriquant. L’idéal est donc de se procurer des condensateurs de précision.
J’espère que cet article vous a plu. Si vous avez des questions n’hésitez pas à les laisser en commentaire !
Références
[1] https://fr.wikipedia.org/wiki/RLC_mètre
[2] https://fr.wikipedia.org/wiki/Step_(fitness)

