Comment utiliser la méthode des tensions de noeud

Nous allons voir dans cet article une méthode de résolution de circuits qui s’appelle la méthode des tensions de noeud (ou méthode des potentiels de noeud). C’est une méthode que j’enseigne à l’Université en cours d’électrotechnique et j’ai eu envie de vous partager cela ici.

La stratégie est simple : on identifie d’abord les noeuds du circuit (je rappelle qu’en électronique un noeud est un recoupement entre plusieurs branches (au moins 3)). On applique ensuite la loi des noeuds de Kirschoff (la somme des courants qui entrent est égale à la somme des courants qui sortent) à chaque noeuds. On obtient ainsi N-1 équation, s’il y a N noeuds. Pourquoi N-1 ? La réponse est un peu plus loin…

Puis on remplace chaque courant par une loi d’Ohm qui fait apparaître la tension au niveau des noeuds.

On obtient donc la tension des N-1 noeuds du circuit.

Et pourquoi N-1 ? Parce que un des noeuds est celui de référence, la masse. On connait donc sa tension, c’est 0V !

Enfin, en utilisant la loi d’ohm de nouveau on déduit le courant de chaque branche avec les tensions de noeuds calculées.

Facile ?

Voyons des exemples.

1 La méthode des tensions de noeud : 1er exemple

Soit le circuit suivant :

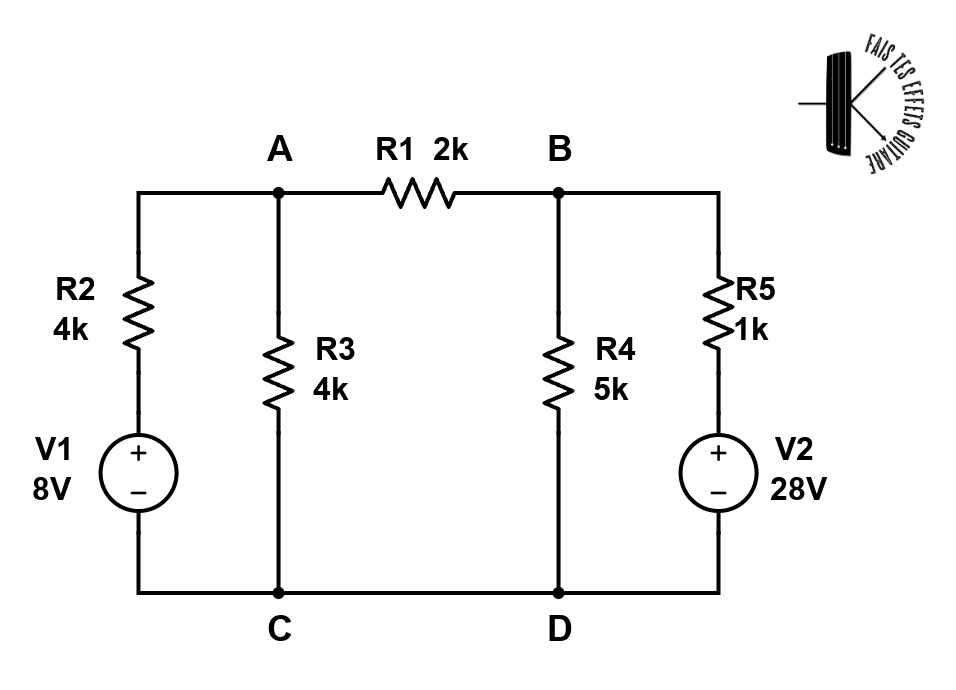
On se propose de calculer la totale : tensions dans tous les noeuds et courants dans toutes les branches. On pourrait faire cela en appliquant la loi des mailles et la loi des noeuds, mais la méthode des tensions de noeud est plus méthodique (d’où le mot méthode) et plus rapide.

1.1 Marche à suivre

Voici le plan à suivre :

• Identifier les noeuds. Soit N leur nombre.
• Choisir un noeud de référence
• Écrire N-1 lois des noeuds
• Transformer les courants en utilisant la loi d’ohm
• Déduire les tensions au niveau des noeuds en résolvant les équations
• Déduire les courants dans les branches en utilisant les tensions trouvées et en appliquant la loi d’Ohm

1.2 Appliquons la méthode

Donc allons-y avec notre exemple :

• Il y a 4 noeuds notés A, B, C et D. Mais C et D sont reliés par un fil. Ils sont au même potentiel et sont en fait un seul et unique noeud C=D. Il y a donc 3 noeuds : A, B et C.
• Le noeud C est connecté au « moins » des sources de tension. Par conséquent il semble naturel de le choisir comme noeud de référence. Mais notez que ce choix est arbitraire et que tout autre choix est valide. On ajoute un signe de masse au noeud C pour savoir que c’est notre référence. Sa tension vaut 0 V. Les autres tensions se mesurent par rapport à elle (la tension de référence).
• N=3, écrivons donc 3-1=2 lois des noeuds, pour les noeuds A et B. Pour cela, aidons nous en dessinant les courants sur le schéma, cela permet de ne pas se tromper sur les signes :

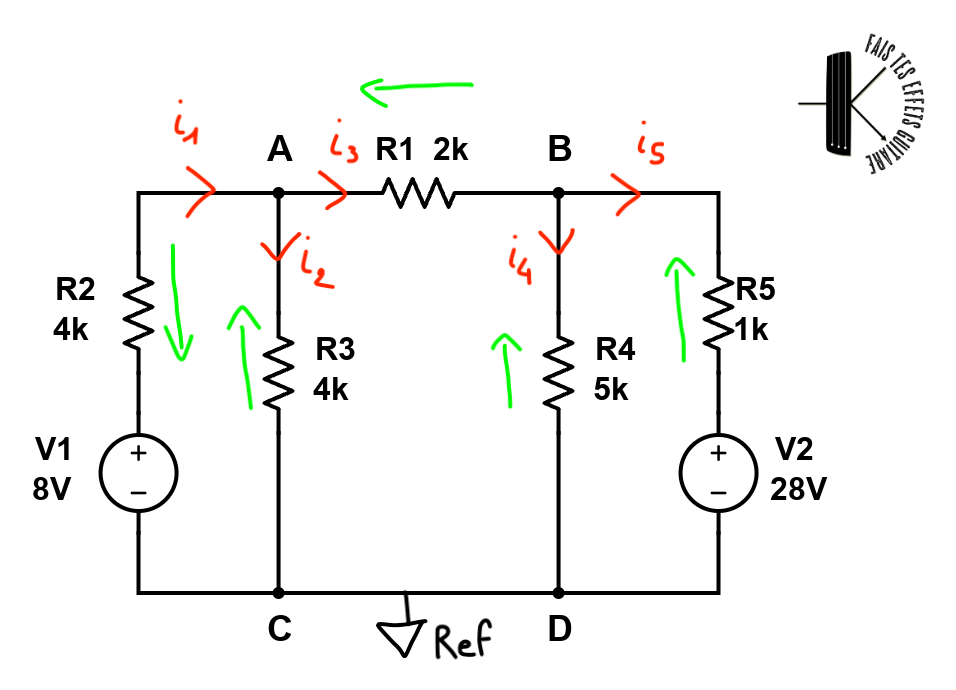
Sur le dessin précédent j’ai ajouté les courants en rouge, les tensions en vert (ça nous servira plus tard) et le symbole de masse en noir en dessous.

Écrivons la loi des noeuds (KCL: Kirschoff Courant Law) en A:

$$i_1=i_2+i_3$$

Facile… Faisons de même en B:

$$i_3=i_4+i_5$$

1.3 Calcul des tensions de Noeuds

Voilà maintenant on exprime chaque courant en fonction des tensions pour faire apparaître les tensions de noeuds qui sont ce qu’on recherche. On notera $V_A$ la tension en A et $V_B$ la tension en B.

Pour cela on utilise la loi d’Ohm. En effet, elle nous dit que la tension aux bornes de la résistance est égale au courant qui la traverse multiplié par la valeur de la résistance. Ça on le sait, mais attention de bien l’appliquer !

Par exemple, si on regarde $R_2$, quelle est la tension à ses bornes ? On regarde la tension sur la pointe de la flèche verte, c’est $V_1$, donc 8 V. Et la tension sur le pied de la flèche c’est la tension en A donc $V_A$. Par conséquent la tension aux bornes de $R_2$ c’est 8-$V_A$.

Or, le courant qui traverse $R_2$ c’est $i_1$ et la résistance de $R_2$ vaut 4 kohms. Par conséquent, en utilisant la loi d’Ohm en exprimant $i$ directement on trouve :

$$\displaystyle i_1=\frac{V_1-V_A}{R2}=\frac{8-V_A}{4k}$$

En faisant de même pour les autres courants, on trouve pour A :

$$\frac{V_1-V_A}{4k}=\frac{V_A}{4k}+\frac{V_A-V_B}{2k}$$

Je réecrie ça en rangeant les $V_A$ d’un côté et les $V_B$ de l’autre, et je multiplie à gauche et à droite par mille pour virer le préfixe $k$ dans les dénominateurs :

$$V_A\left(\frac{1}{4}+\frac{1}{2}+\frac{1}{4}\right)=\frac{V_1}{4}+\frac{V_B}{2}$$

Soit, sachant que $V_1=8V$ :

$$V_A=2+\frac{V_B}{2}$$

Faisons de même pour le noeud B :

$$\frac{V_A-V_B}{2k}=\frac{V_B}{5k}+\frac{V_B-V_2}{1k}$$

Je remplace $V_A$ par l’expression qu’on a trouvée (en ayant préalablement simplifié les $k$ comme avant) :

$$1+\frac{V_B}{4}-\frac{V_B}{2}=\frac{V_B}{5}+\frac{V_B-V_2}{1}$$

Et en rangeant on trouve :

$$1+V_2=V_B\left(\frac{1}{5}+1+\frac{1}{4}\right)$$

Soit, en remplaçant $V_2$ par 28 V:

$$V_B=\frac{29}{20}(1+V_2)=\frac{29}{20}(1+28)=20 V$$

Puis on injecte le résultat de $V_B$ dans l’équation qui donne $V_A$ :

$$V_A=2+\frac{V_B}{2}=2+\frac{20}{2}=12 V$$

Super ! On a trouvé la tension en A (12 V) et en B (20 V).

1.4 Calcul des courants de branches

On peut passer à la dernière étape : déduire les courants dans les branches en utilisant la loi d’Ohm.

Cependant, ayant déjà détaillé le calcul plus haut, je donne le calcul directement :

$$
\begin{array}{l}
\displaystyle i_1=\frac{V_1-V_A}{4k}=\frac{8-12}{4k}=-1mA\\
\displaystyle i_2=\frac{V_A}{4k}=\frac{12}{4k}=3mA\\
\displaystyle i_3=\frac{V_A-V_B}{2k}=\frac{12-20}{2k}=-4mA\\
\displaystyle i_4=\frac{V_B}{5k}=\frac{20}{5k}=4mA\\
\displaystyle i_5=\frac{V_B-V_2}{1k}=\frac{12-20}{1k}=-8mA
\end{array}
$$

On trouve des courants négatifs, c’est normal. En effet, cela signifie que le sens que l’on a choisit sur le dessin n’était pas le bon pour avoir un courant positif, mais ça ne veut pas dire que c’est faux ! Ça veut dire que si on veut des intensités positives, il faut dessiner la flèche dans l’autre sens. D’autre part on ne pas savoir le sens des flèches avant d’avoir calculé le courant.

Finalement je récapitule tous les résultats sur le schéma suivant que j’ai simulé avec LTSpice :

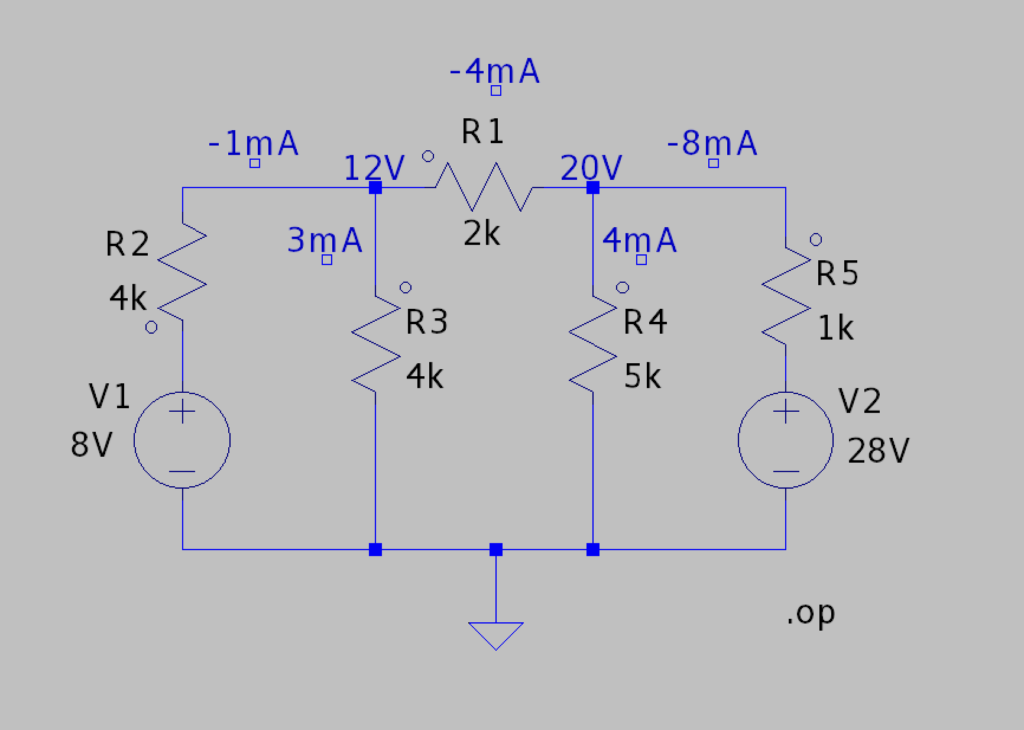
Voilà, vous connaissez la méthode des tensions de noeud. Avant de passer à un exemple concret, voyons un concept utile.

2 Concept de super-noeud

2.1 Explication du concept de super-noeud

Soit la figure suivante :

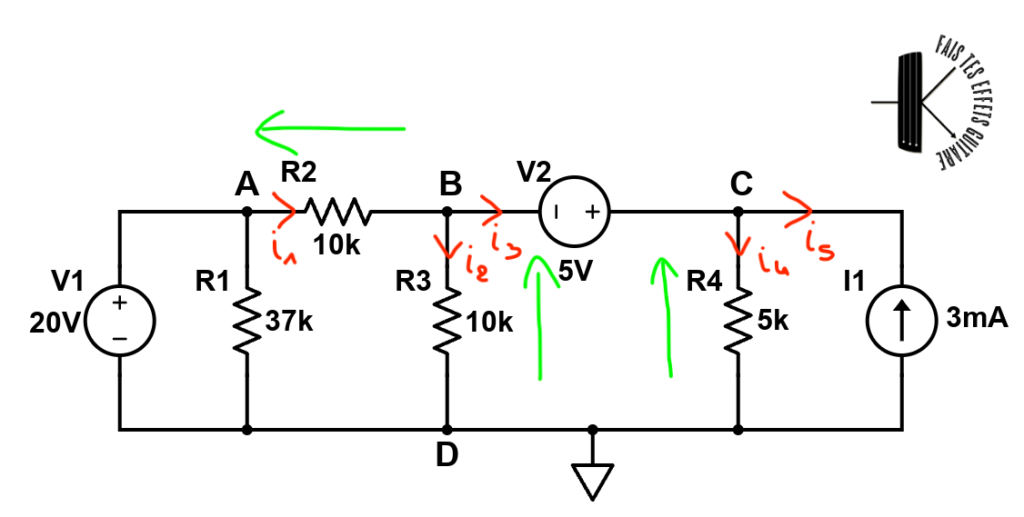
On voit que c’est un peu le schéma d’avant, mais il y a une grosse différence, il y a une source de tension au milieu.

Est-ce plus compliqué ?

Non, il suffit d’appliquer la méthode des tensions de noeud comme vu jusqu’ici. Ainsi, si on choisit le noeud D comme noeud de référence, il reste à appliquer la méthode sur les 3 noeuds restant A, B et C.

En A en fait il n’y a pas besoin de chercher, A est connecté à la source de tension de gauche, donc sa tension est 10V.

Il ne nous reste donc qu’à appliquer 2 lois de Kirschoff en courant (ou loi des noeuds) en B et en C.

En B : $i_1=i_2+i_3$

Et en C : $i_3=i_4+i_5$

On remarque d’ailleurs que $i_5=-3 mA$ car $i_5$ est le courant débité par la source de courant, à droite, mais dans le sens inverse.

Et si on remplace l’expression de $i_3$ dans l’expression trouvée en B, on a que $i_1=i_2+i_3=i_2+i_4+i_5$

Tout se passe comme si on avait joint les noeuds B et C en un seul noeud. C’est ce qu’on appelle un super-noeud.

Le concept de super-noeud est le suivant : ce n’est pas un super pouvoir. Lorsque 2 noeuds sont reliés par une source de tension (indépendante ou dépendante ça marche aussi), on peut faire comme si les 2 noeuds étaient reliés entre eux par un fil. Soit B=C. On applique alors directement la loi des noeuds sur le supernoeud B-C : $i_1= i_2+i_4+i_5$.

Mais il faudra rajouter une équation qui tient en compte la source de tension que l’on a subtilement évincé. Et dans le cas présent cette équation est : $V_C-V_B=5 V$.

2.2 Résolution du circuit en utilisant le super-noeud

Je reproduis sur la figure suivante le circuit en symbolisant le super noeud B-C en pointillé :

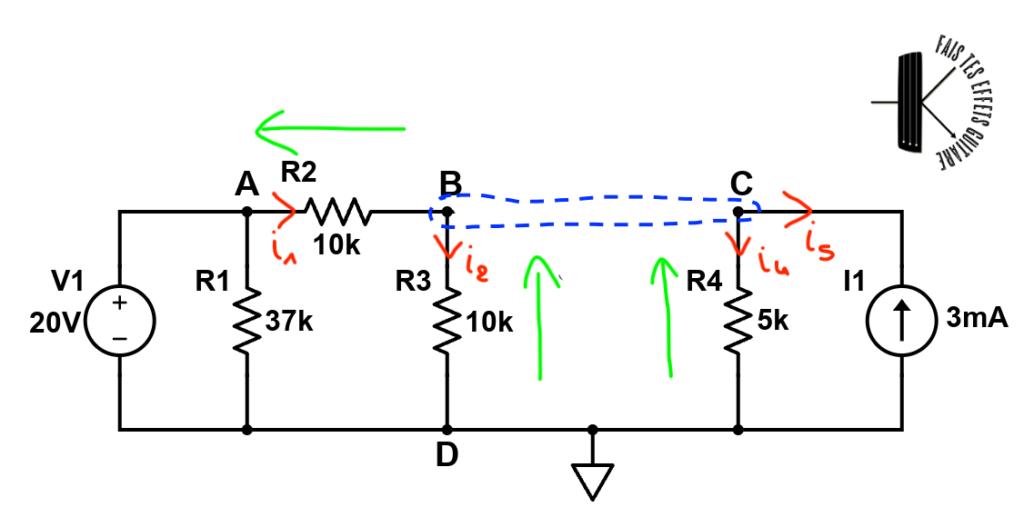
Dans la technique du super-noeud on fait la chose suivante :

• on enlève la source de tension entre les 2 noeuds, donc ici B et C. Et on suppose que B est relié à C avec un fil pour faire la loi des noeuds,
• on ajoute en plus l’équation de la source qu’on a enlevé.

Nous savons que $V_A=0 V$, $V_D=0 V$. Écrivons la loi des noeuds pour le super noeud et l’équation pour la source de tension du super-noeud:

$$
\begin{array}{l}
i_1=i_2+i_4+i_5\\
V_B-V_C=5
\end{array}
$$

Puis, remplaçons les courants par les potentiels au niveau des noeuds :

$$\displaystyle \frac{20-V_B}{10k}=\frac{V_B}{10k}+\frac{V_C}{5k}-3m$$

En réarrangeant on trouve que :

$$V_B+V_C=25$$

Or l’équation de la source nous a donné :

$$V_B-V_C=5$$

Nous avons donc 2 équations pour 2 inconnues, on peut donc trouver $V_B$ et $V_C$ et on trouve :

$$
\begin{array}{l}
V_B=15 V\\
V_C=10 V
\end{array}
$$

Puis, de même que précédemment, on peut maintenant déduire les courants dans chaque branche. Remarquons avant que la résistance de 37k n’intervient pas dans le calcul. C’est pour cela que je lui ai donné une valeur « random » alors que je me suis arrangé pour donner des valeurs rondes aux autres paramètres.

Voici donc les valeurs des courants :

$$
\begin{array}{l}
\displaystyle i_1=\frac{V_A-V_B}{10k}=1 mA\\
\displaystyle i_2=\frac{V_B}{1k}=1 mA\\
\displaystyle i_4=\frac{V_C}{5k}=3 mA\\
\displaystyle i_5=-3 mA
\end{array}
$$

Pour finir voyons un application de tout cela sur un transistor.

3 LA méthode des tensions de noeud : 2eme exemple

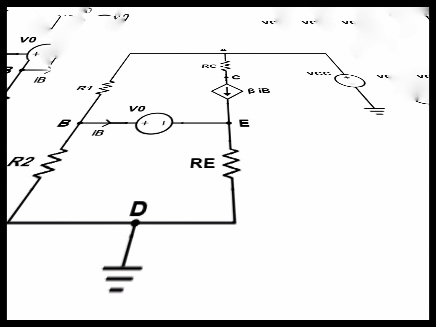
Prenons un circuit connu de la littérature des faiseurs d’effet, par exemple un boost à transistor LPB-1 (vous pouvez télécharger un guide qui vous explique comment le fabriquer ici (c’est gratuit !)) :

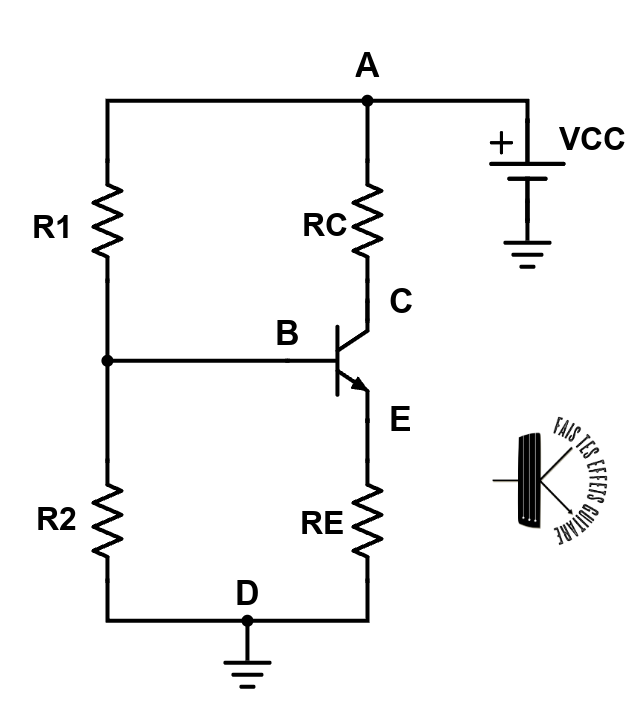
Par exemple, ce qu’on peut vouloir, c’est avoir une tension de collecteur (point C sur la figure ci-dessus) à $V_{CC}/2$ pour permettre d’avoir un boost le plus linéaire possible (je traduis pour les guitaristes : le plus clean possible 😊).

3.1 Redessinons le schéma électrique

On peut schématiser ce montage à l’aide de sources de tension et de courant. En particulier, on sait que lorsque le transistor est dans la région active :

• la jonction base-émetteur est toujours à 0,65 V (voir l’article sur la jonction PN pour plus de détails).
• Le courant de collecteur $i_C$ est proportionnel au courant de base $i_B$ : $i_C=\beta i_B$ avec $\beta$ le gain en courant, caractéristique du transistor.

Sachant cela on peut dessiner un schéma équivalent avec une source de tension constante $V_0=0,65 V$ et une source de courant dépendente en courant telle que le courant fournit $i_C=\beta i_B$ (pour plus de détails consulter la référence [Nilsson]) :

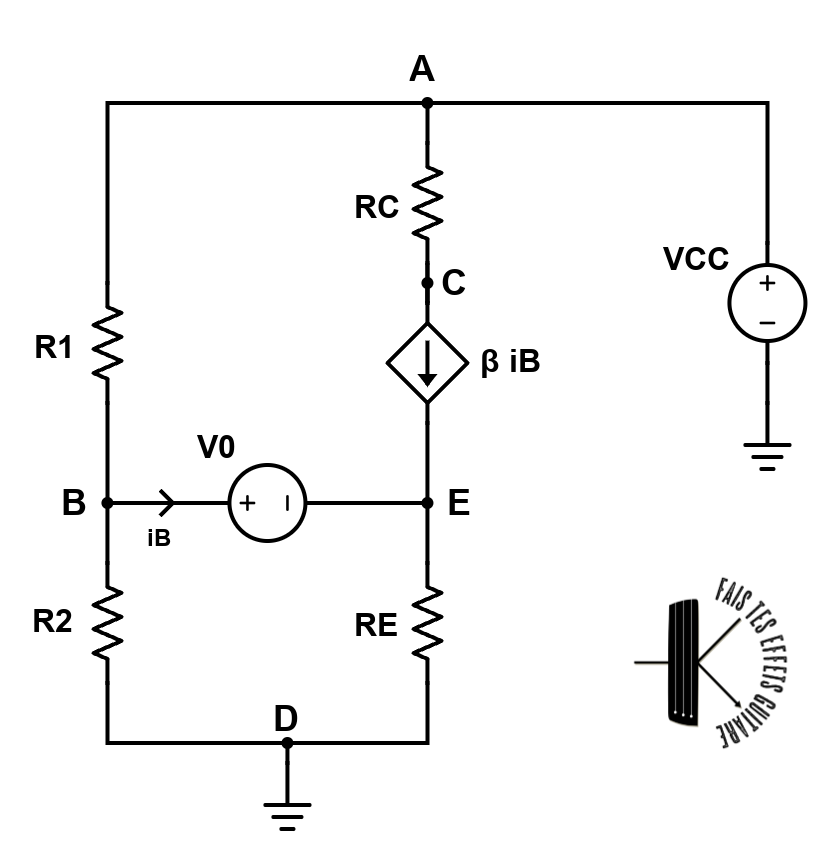
Dans ce circuit il y a 6 inconnues . En effet, nous avons $i_1$ passant dans $R_1$, $i_2$ passant dans $R_2$, $i_E$ passant dans $R_E$, $i_B$, $i_C$ passant dans $R_C$et $i_{CC}$ débité par la pile.

En utilisant les lois de Kirchoff (loi des noeuds et loi des mailles), on obtient 5 équations. Puis en utilisant que dans le transistor $i_c=\beta i_b$ on obtient une 6è équation.

6 équations, 6 inconnues, on doit donc pouvoir résoudre ce circuit. En effet, après un peu de travail on trouve :

$$\displaystyle i_B=\frac{\frac{V_{CC}R_2}{R_1+R_2}-V_0}{\frac{R_1 R_2}{R_1+R_2}+(1+\beta)R_E}$$

C’est bien, mais c’est un peu laborieux (je traiterai cette résolution dans un autre article).

3.2 Appliquons la méthode des tensions de noeud

Recherchons ce résultat en appliquant la méthode des tensions de noeud.

Analysons les noeuds :

En A : c’est facile, A est connecté à $V_{CC}$ donc $V_A=V_{CC}$.

En D : c’est notre noeud de référence, $V_D=0 V$.

La lettre C n’est pas vraiment un noeud, je l’ai mis pour indiquer l’électrode de collecteur dans le modèle. On en aura besoin par la suite pour calculer son potentiel.

Il reste à calculer les tensions aux noeuds B (base) et E (émetteur) puis on en déduira la tension en C.

Nous pouvons noter que B et C sont connectés par une source de tension. On peut donc utiliser le concept de super-noeud :

• B=C, on applique la loi des noeuds comme si B et C étaient le même noeud
• On ajoute l’équation de la source évincée pour la tenir en compte

Voici le schéma redessiné avec le super-noeud et les courants utilisés (leur sens est arbitraire mais le résultat final est indépendant du sens choisi) :

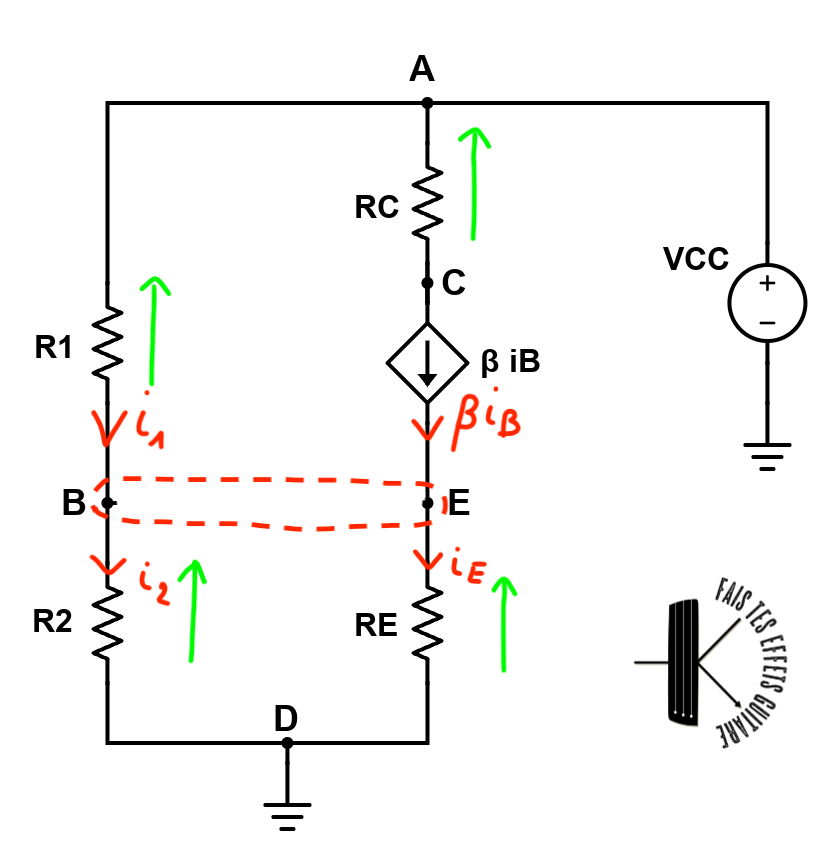
J’ai également dessiné les tensions aux bornes des résistances en vert, pour ne pas se tromper dans les signes après.

Nous avons donc les 2 équations suivantes, loi des noeuds dans le super noeud B-E et équation de la source $V_0$ :

$$
\begin{array}{lr}
i_1-i_2-i_E+\beta i_B=0 & (1)\\
V_0=V_B-V_E & (2)
\end{array}
$$

Puis, à cela on rajoute l’équation du transistor qui relie $i_B$, $i_C$ et $i_E$ (courants de base, collecteur et émetteur respectivement) :

$$
\begin{array}{lr}
i_E=i_B+i_C & (3)
\end{array}
$$

On a donc 3 équations avec lesquelles on va pouvoir trouver ce qui nous intéresse, c’est à dire la tension de base (noeud B) dans un premier temps, puis la tension de collecteur (point C) dans un second.

3.4 Cherchons l’expression du potentiel en B

Revenons à la 1ère équation et exprimons $i_1$, $i_2$ et $i_E$ en fonction des résistances qu’ils parcourent et des tensions aux bornes des résistances. On trouve alors que :

$$
\begin{array}{ccc}
(1) & \Leftrightarrow & \displaystyle \frac{V_{CC}-V_B}{R_1}-\frac{V_B}{R_2}-\frac{V_E}{R_E}+\beta i_B =0
\end{array}
$$

Dans cette équation nous voulons exprimer $V_B$ en fonction du reste des paramètres, donc on le garde. Par contre, il faut exprimer $V_E$ et $i_B$ en fonction du reste.

$$
\begin{array}{ccc}
(2) & \Leftrightarrow & \displaystyle V_E=V_B-V_0
\end{array}
$$

Voilà pour $V_E$. Et pour $i_B$ :

$$
\begin{array}{ccc}
(3) & \Leftrightarrow &i_E= i_B + \beta i_B \\
& \Leftrightarrow & i_E= i_B (1 + \beta)
\end{array}
$$

Or en appliquant la loi d’Ohm on trouve que $i_E=\frac{V_E}{R_E}$

Par conséquent : $$i_E= i_B (1 + \beta)=\frac{V_E}{R_E}$$

Donc $$i_B=\frac{V_E}{R_E (1+ \beta)}$$

On remplace comme prévu $V_E$ et $i_B$ dans l’équation trouvée plus haut. On trouve :

$$
\begin{array}{cl}
& \displaystyle \frac{V_B}{R_2}+\frac{V_B}{R_1}-\frac{V_{CC}}{R_1}+\frac{V_B-V_0}{R_E}-\beta \frac{V_B-V_0}{R_E (1+\beta)}=0 \\
\Rightarrow & \displaystyle \frac{V_B}{R_2}+\frac{V_B}{R_1}-\frac{V_{CC}}{R_1}+\frac{V_B-V_0}{R_E} \left(1-\frac{\beta}{ 1+\beta}\right)=0\\
\Rightarrow & \displaystyle \frac{V_B}{R_2}+\frac{V_B}{R_1}-\frac{V_{CC}}{R_1}+\frac{V_B-V_0}{R_E} \frac{1}{ (1+\beta)}=0\\
\Rightarrow & \displaystyle V_B\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_E(1+\beta)}\right)=\frac{V_{CC}}{R_1}+\frac{V_0}{R_E}\frac{1}{1+\beta}\\
\Rightarrow & \displaystyle V_B \frac{(R_2+R_1)R_E(1+\beta)+R_1 R_2}{R_1 R_2 R_E (1+\beta)}=\frac{V_{CC}R_E (1+\beta) + V_0 R_1}{R_1 R_E (1+\beta)}\\
\Rightarrow & \displaystyle V_B=\frac{V_{CC}R_E(1+\beta)R_2 + V_0 R_1 R_2}{R_E (1+\beta)(R_1 + R_2) + R_1 R_2}
\end{array}
$$

Oufff, ça y est on a l’expression de $V_B$ (et je vous laisse vérifier que l’on retrouve bien l’équation de $i_B$ vue en 3.1 en utilisant l’expression de $i_B$ trouvée quelques lignes plus haut).

3.5 Déduisons l’expression de la tension $V_C$

Ce qu’on veut c’est $V_C$. Et $V_C$ c’est facile car en utilisant la loi d’Ohm :

$$V_C=V_{CC}-R_C i_C$$

En exprimant $i_C$ en fonction de $i_E$ on trouve finalement que :

$$V_C=V_{CC}-\frac{R_C}{R_E} (V_B-V_0)\frac{\beta}{\beta +1}$$

Et on remplacera $V_B$ dans cette expression par la grosse expression qu’on a trouvé pour elle.

Application numérique

Avec les valeurs du boost de Electro-Harmonix LPB-1, R1=430k, R2=43k, RC=10k, RE=390 ohms, VCC=9V je trouve en insérant ces valeurs dans les expressions trouvées pour $V_B$ et $V_C$ :

• $V_B$=0,81 V
• $V_C$=4,97 V

On constate que $V_C$ est pas mal proche de 4,5 V, c’est ce qu’on voulait pour faire un boost clean.

Pour finir de s’en convaincre j’ai fait une simulation avec le simulateur LTSpice :

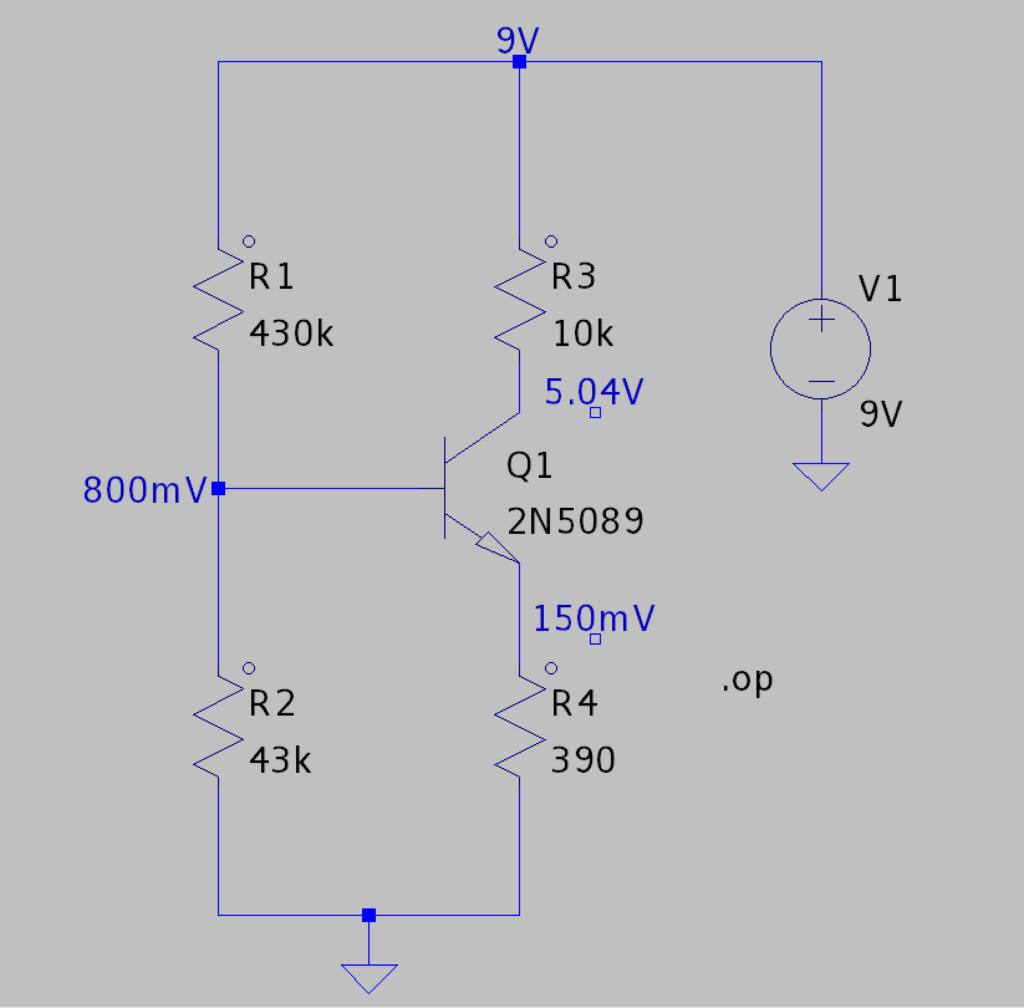
On voit que $V_B$=800 mV=0,8 V, proche de nos 0,81 V. Et pour $V_C$ on trouve 5,04 V, un écart de 1,3 % avec la valeur donnée par le calcul, donc ça va, le calcul a l’air correct ! (Je précise que LTSpice utilise un modèle de transistor différent de celui étudié ici, d’où les petites variations).

Conclusion

Nous avons vu la méthode de tension de noeuds, utile pour trouver les courants et les tensions dans un circuit. Nous avons vu la démarche à suivre sur différents circuits dont un amplificateur à transistor. Je suis allé un peu vite pour le calcul final de $V_C$ parce que j’ai commencé à avoir mal au dos avec tant de formules. Mais si vous avez des questions n’hésitez pas à les mettre en commentaire !

Références
[Nilsson] Nilsson and Riedel, Electric circuits, Global Edition