Dans cet article nous parlons de spectre. Non pas de l’organisation criminelle contre laquelle lutte James Bond…
Mais de la notion de spectre qui découle de la décomposition en série de Fourier d’un signal.
Nous sommes peut-être plus habitués à nous représenter l’évolution d’un signal avec le temps. C’est ce que mesure un oscilloscope par exemple.
Cependant, la connaissance des fréquences qui composent un signal est indispensable en électronique. En audio, ceci permet de comprendre la nature du son et de savoir comment le traiter artificiellement.
Dans cet article, nous allons voir ce qu’est la définition du spectre (en électronique donc) et sans entrer trop en détail je vais présenter le concept de série de Fourier.
Puis je donnerai quelques exemples de décomposition en série de Fourrier, sur une mesure et par le calcul.
Sommaire
1 Définitions, spectre et série de Fourier
1.1 Fréquence et amplitude
Nous avons déjà mentionné dans l’article Résistance d’entrée/sortie et effet sur l’amplitude du signal transmis comment se crée le son en sortie d’une guitare électrique, sa propagation, son amplification puis sa restitution par un haut parleur.
Nous avons alors été amenés à définir 2 caractéristiques de l’onde : sa fréquence et son amplitude.
Rappelons brièvement leur définition :
- D’après [1] : « La fréquence $f$ représente le nombre de fois qu’une fonction (courant, tension ou puissance) se répète identiquement à elle-même en une seconde. Il s’agit donc pour un signal périodique du nombre de périodes par seconde. L’unité est le hertz (Hz). »
$f =\frac{1}{T}$, avec $T$ la période exprimée en secondes.
- L’amplitude mesure l’ampleur de la variation de la fonction qui nous intéresse [2].
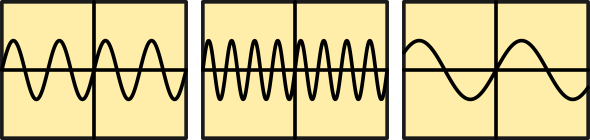
Voici 3 exemples d’oscillogrammes tracés à la même échelle. On voit que l’amplitude est la même, mais la fréquence est différente. Si on prend la courbe de gauche comme référence, la courbe du milieu a une fréquence plus élevée et la courbe de droite une fréquence plus petite.
La gamme de fréquence qui nous intéresse en audio est celle qui correspond aux fréquences audible par l’homme. Cette gamme va de 20 Hz à 20000 Hz, et se considère comme de la basse fréquence.
1.2 Série de Fourier
1.2.1 Notion de timbre
Si nous écoutons une même note, par exemple un la 440, jouée par 3 instruments de musique différents, nous entendrons la même note, mais avec un son différent. Pourquoi?
C’est parce que lorsque ce « la » est joué, l’air vibre essentiellement 440 fois par seconde. On appelle cette fréquence la fréquence fondamentale. Mais la nature de l’instrument (ses dimensions, son matériel, sa caisse de résonance, etc…) font que d’autres fréquences, qui sont permises par les lois de la physique, résonnent avec plus ou moins d’amplitude. Voyons cela de plus près.
En mesurant le son du « la » avec un micro, on peut regarder la forme du signal avec le temps. Voici par exemple un oscillogramme que j’ai mesuré dans l’article Comment faire sonner sa guitare comme un synthétiseur? :
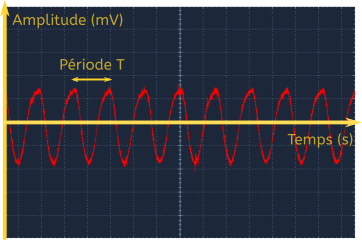
J’ai obtenu cet oscillogramme en jouant un mi à la 12e case de la corde de mi aigu. En théorie, cette fréquence est de 660 Hz.
Sur l’oscillogramme, on mesure la fréquence obtenue en Hz en mesurant la période en secondes puis en prenant son inverse.
On mesure une période de 1,52 ms donc une fréquence de 1/1,52m=657 Hz.
Cependant, on voit que la courbe n’est pas exactement une sinusoïde. Elle est un peu « cabossée » sur ses maxima.
Ceci est due, comme on vient de le voir à la nature complexe de l’onde, elle n’est pas une simple sinusoïde comme l’est un son pur, sinon une somme de sinusoïdes ayant :
- différentes amplitudes (ou poids),
- une fréquence multiple de la fréquence fondamentale.
Le poids de la fréquence fondamentale domine, bien sûr, et détermine la hauteur perçue de la note. L’amplitude des autres fréquences que l’on appelle harmoniques détermine le timbre du son.
En résumé, on peut décrire une onde complexe en une somme de sinusoïdes de différents poids.
1.2.2 Définition mathématique
On peut, connaissant le signal en fonction du temps, comme l’oscillogramme montré ci-dessus, trouver toutes les fréquences comprises dans le signal et leur amplitude. On fait pour cela un développement en série de Fourier [3] du signal.
Cela revient à dire mathématiquement pour une fonction f(t) de période T :
$$ f(t)= a_0 + \sum_{n=1}^{\infty}\left(a_ncos(2\pi n f t)+b_n sin(2\pi n f t)\right)$$
Le symbole $\sum$ signifie que l’on somme toutes les sinusoïdes comprises dans les parenthèses. $a_n$ et $b_n$ sont les coefficients des fonctions sinusoïdales (ou amplitude, ou poids). Et $n$ est un nombre entier qui varie de 1 à l’infini.
Les coefficients se trouvent par le calcul, je vous donne leur expression. C’est des mathématiques assez compliqués qui font appel au calcul intégral et qui sortent du cadre de ce blog. Tout de même, je donnerai un exemple d’application plus loin dans un cas simple.
$$
\left\{
\begin{array}{l}
a_0=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t)dt\\
a_n=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t)cos(n\omega t)dt\\
b_n=\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t)sin(n\omega t)dt
\end{array}
\right.
$$
$\omega$ est la pulsation, et $\omega=2\pi f$.
Il est également possible d’utiliser un algorithme sur ordinateur pour trouver les coefficients, à l’aide d’une FFT (Fast Fourier Transform pour Transformation de Fourier rapide) [4]. Cet outil est en général disponible sur les programmes de traitement de données et permet d’analyser les mesures de signal réalisées très rapidement. Nous allons également voir un exemple dans la suite.
1.3 Spectre et harmoniques
On pourra alors tracer un graphique donnant l’amplitude de chaque sinusoïde $a_n$ et $b_n$ en fonction de sa fréquence $n\times f$. On passe donc du domaine temporel au domaine fréquentiel, et le graphique que l’on obtient s’appelle : un spectre.
Voici par exemple le spectre du signal de guitare mesuré plus haut que j’obtiens, en réalisant l’analyse de Fourier FFT sur ce signal :
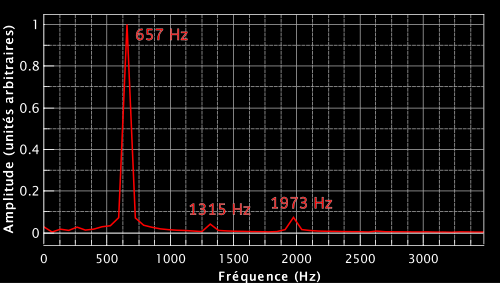
La 1ère chose qu’on voit est qu’on passe d’une représentation amplitude-temps à amplitude-fréquence. On lit donc une fréquence sur l’axe des abscisses.
On voit bien que la fréquence fondamentale est de 657 Hz ($n$=1), c’est bien la fréquence du mi 12e case de la corde de mi aiguë. À ce son pur s’ajoutent les harmoniques, de moindre poids, et de fréquence 1315 Hz ($n$=2) et 1973 Hz ($n$=3).
On remarque de plus que 1315 ~ 2×657 et que 1973 ~ 3×657. On voit donc expérimentalement que les harmoniques ont une fréquence multiple de la fréquence fondamentale.
Finalement, les plus assidus d’entre vous s’interpelleront sur le fait de si on peut reproduire le signal original à partir du spectre ? La réponse est oui, mais…
2 Spectres typique en électronique
Voici 3 exemples d’analyse spectrale, pour des signaux connus : un son pur, un signal carré et un signal en dents de scie.
2.1 Étude spectrale d’un son simple (ou pur)
Un son est dit simple ou pur lorsque l’onde est parfaitement sinusoïdale. On ne la trouve pas dans la nature, mais on peut la produire avec un générateur d’onde sinusoïdal et un haut-parleur.
Mathématiquement on l’écrit sous la forme suivante :
$$f(t)=A_0\sin(2\pi f t)$$ avec $A_0$ son amplitude et $f$ sa fréquence.
Voici la représentation de f dans le temps et son spectre :
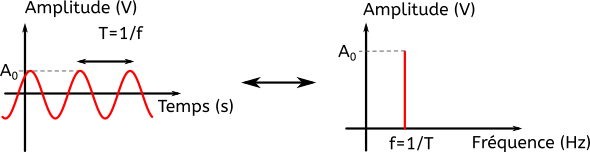
La fonction f(t) est définie par une sinusoïde dont on connaît l’amplitude et la fréquence. Par conséquent son spectre est trivial, c’est un unique « bâton » localisé à la fréquence f=1/T.
Un son simple n’a donc pas d’harmoniques.
2.2 Signal carré
Sur la figure suivante je montre un signal carré :

Je l’ai défini de manière à ce qu’il oscille entre les valeurs a et -a, sa période est T. La fonction f(t) est donc définie comme suit :
$
f(t) = \left\{ \begin{array}{rrl} -a & de & \left]-\frac{T}{2};0 \right[ \\ a & de & \left]0;\frac{T}{2}\right[ \end{array} \right.
$
Rappelons la définition de la série de Fourier :
$$
f(t)= a_0 + \sum_{n=1}^{\infty}\left(a_ncos(2\pi n f t)+b_n sin(2\pi n f t\right))
$$
On voit que la fonction carrée telle que je l’ai dessinée est une fonction impaire, c’est-à-dire symétrique par rapport à l’origine (0;0). Ceci implique que $a_0$ et tous les $a_n$ sont nuls. En effet, faire une intégrale signifie calculer l’aire sous la courbe. Dans le cas de $a_0$ on somme à gauche et à droite de l’ordonnée deux aires égales de signe opposé. L’aire totale est donc nulle. Pour les $a_n$, c’est la même chose car la fonction cosinus est paire. Par conséquent $f(t) \times \cos(n\omega t)$ est une fonction impaire, c’est à dire symétrique par rapport à l’origine. Pour les mêmes arguments que pour le calcul de $a_0$, les $a_n$ sont donc tous nuls.
Il ne faut donc que calculer les coefficients $b_n$ !
$$
\begin{array}{rcl}
b_n & = & 2\times \frac{2}{T}\int_{0}^{\frac{T}{2}} a\sin(n\omega t)dt \\
& =& \frac{4}{T}(-\frac{a}{n\omega})[cos(n\omega t)]_0^\frac{T}{2} \\
& =& -\frac{4}{T}\frac{a}{n\omega}(cos(n\pi)-1) \\
& =& \frac{2a}{n\pi}(1-(-1)^n)
\end{array}
$$
On trouve donc pour les coefficients de la série de Fourier que $b_1=\frac{4A}{\pi}$, $b_2=0$, $b_3=\frac{4A}{3\pi}$, $b_4=0$, $b_5=\frac{4A}{5\pi}$,…
Et finalement on trouve pour la décomposition de la fonction carrée en somme de fonctions sinus :
$$
f(t)=\frac{4a}{\pi}(sin(\omega t)+\frac{1}{3}sin(3\omega t)+\frac{1}{5}sin(5\omega t)+\frac{1}{7}sin(7\omega t)+…
$$
La somme va, par définition, jusque l’infini…
Finalement, voici le spectre de la fonction carrée que l’on a obtenu par le calcul :
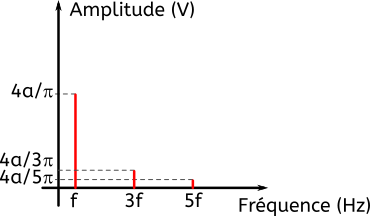
2.3 Pourquoi je vous ai raconté tout cela sur la fonction carré ?
Dans l’article intitulé Comment faire sonner sa guitare comme un synthétiseur ?, je vous avez montré que lorsque le signal quasi-sinusoïdal franchit la porte logique, il devient carré.
Ah…
Une distorsion, ce qu’elle fait, c’est cela, aplanir les maxima du signal. Elle conduit donc à ajouter des harmoniques dans le signal, des fréquences plus aiguës donc.
Et dans le cas d’une fuzz, le signal est très aplani, quasiment carré. On fait donc apparaître tout une foule d’harmoniques ce qui change le timbre et explique pourquoi on ne reconnaît plus le son de la guitare.
Fabriquer un pédale d’effet de type overdrive, distorsion ou fuzz, c’est donc travailler sur le spectre du signal. On peut ensuite travailler sur la forme du spectre à l’aide de filtres.
2.4 Signal en dents de scie
Voici un dernier exemple de spectre, pour la fonction dents de scie définie comme suit :
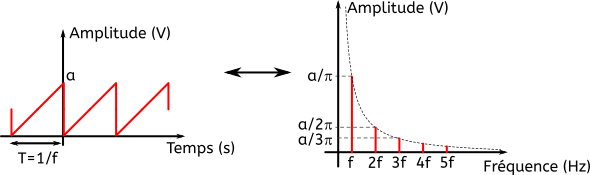
Le spectre est donné à droite. Je vous épargne le calcul ! Celui-ci montre que le spectre est semblable au spectre de la fonction carré, mais avec les fréquences paires en plus (2f, 4f, etc…).
Vous avez des questions ? N’hésitez pas à les poser dans les commentaires !
Références
[1] « L’électronique de A à Z« , Tahar Neffati, éd. Dunod
[2] https://fr.wikipedia.org/wiki/Amplitude
[3] https://fr.wikipedia.org/wiki/S%C3%A9rie_de_Fourier
[4] https://fr.wikipedia.org/wiki/Transformation_de_Fourier_rapide
