Nous avons déjà vu le concept de diagramme de Fresnel dans ce blog. En effet, dans cet article, j’avais adopté un formalisme mathématique assez poussé pour traiter le cas du circuit RC.
Dans le présent article, je donne un point de vue plus basique et général, en expliquant les bases de la construction du diagramme de Fresnel pour une résistance, un condensateur ou une bobine. Puis nous verrons son application dans le cas du circuit RLC série. Nous déterminerons l’amplitude de la tension de sortie, le déphasage entre courant et tension d’entrée et le gain du circuit. Vamos !
Sommaire
1 Intérêt du diagramme de Fresnel
1.1 Problème
Imaginons dans un 1er temps un circuit composé de résistances et d’une source de tension continue. Nous sommes donc en régime continu.
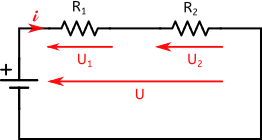
Par conséquent, la tension aux bornes de chaque résistance est constante : $U_1=$cst et $U_2=$cst.
Puisque les tensions ne varient pas avec le temps, on peut allègrement les sommer pour avoir la tension $U$ aux bornes des deux résistances :
$U=U_1+U_2$
Pas de problème jusqu’ici.
Imaginons maintenant que l’on remplace la source de tension continue par une source de tension sinusoïdale. La tension délivrée par la source varie avec le temps, par conséquent, la tension aux bornes des résistances aussi. On rajoute donc la lettre $t$ à l’affaire :
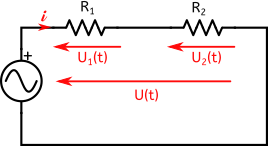
Dans ce cas là il n’y a pas non plus de souci lorsque l’on somme les tensions, car $U_1(t)$ et $U_2(t)$ sont en phase (nous verrons plus loin que les résistances n’apportent pas de déphasage).
Par conséquent si on veut l’amplitude de la tension $U(t)$, on fait simplement la somme des amplitudes de $U_1(t)$ et de $U_2(t)$.
Tout se complique lorsque $U_1(t)$ et $U_2(t)$ ne sont plus en phase. Regardons par exemple le circuit suivant :
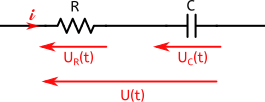
Dans cette portion de circuit nous avons maintenant une résistance et un condensateur. La tension à leurs bornes est respectivement $U_R(t)$ et $U_C(t)$.
Peut-on sommer l’amplitude de ces 2 tensions pour obtenir l’amplitude de $U(t)$ la tension totale ? Et bien surtout pas !!!
Regardons ce que donne chacune des tensions :
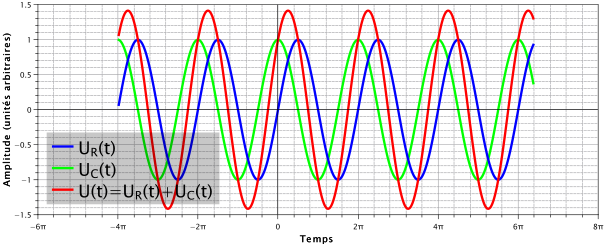
Regardez les courbes verte et bleue, ce sont (supposons le) les tensions aux bornes de R et de C. On voit 2 sinusoïdes, de même fréquence. Leur amplitude est de 1, et leurs maxima ne coïncident pas.
Et comme je l’ai dit plus haut, le problème c’est le déphasage entre ces 2 tensions.
J’ai obtenu la courbe rouge en sommant les courbes verte et bleue. On voit que son amplitude est de environ 1,4. L’amplitude ne vaut donc pas 1+1, la somme des amplitudes des 2 autres courbes.
On voit également que la courbe rouge est déphasée par rapport aux 2 autres.
Par contre sa fréquence est la même.
1.2 Solution
Peut-on obtenir les informations de la courbe rouge, c’est-à-dire son amplitude et sa phase sans faire de calcul sur les sinusoïdes ?
Oui.
En effet, vous pouvez utiliser les formules de trigonométrie, ou le formalisme des nombres complexes. Dans le cas de ce dernier, c’est un formalisme pas forcément évident, mais qui, une fois qu’on le connaît, fait que tout est beaucoup plus facile. J’en parle dans cet article sur les nombres complexes.
Mais il y a une autre méthode qui consiste à représenter les tensions et les intensités dans le plan en se plaçant à $t=0$.
Et oui ! Nos inconnues sont amplitude et phase. Vu qu’il y a 2 inconnues, en travaillant à 2 dimensions on s’en sort graphiquement !
Mais alors, en cartésien ou en polaire ? En polaire !
On va associer la sinusoïde à un vecteur. Son module (sa longueur) est associée à l’amplitude, et l’angle que fait le vecteur avec l’axe des abscisses donne la phase.
Cette méthode graphique va nous permettre de traiter certains cas assez simples comme les filtres RC, LR, RLC série et parallèle, voire des choses un peu plus chiadées… Elle va nous faciliter la vie pour trouver les déphasages entre grandeurs, pour calculer la puissance, les impédances… On pourra même calculer le gain d’un circuit avec cette méthode.
Voyons cela de plus près.
2 Amplitude et déphasage d’éléments isolés
Nous allons étudier graphiquement le cas de la résistance, du condensateur et de la bobine. Supposons qu’un courant alternatif sinusoïdal passe dans chaque composant :
$i(t)=I_m \cos (\omega t)$, avec $I_m$ l’amplitude du courant et $\omega$ sa pulsation (on se souvient que $\omega=2\pi f$).
2.1 Résistance
Considérons d’abord la résistance :

Étudions la tension à ses bornes $U_R(t)$. Cette tension est sinusoïdale, de même pulsation que le courant car on est en régime sinusoïdale forcé (forcé par le générateur). Ça, c’est ce qu’on sait.
Par conséquent, $U_R(t)$ est de la forme :
$U_R(t)=U_{R_m} \cos(\omega t + \varphi_R)$.
On cherche l’amplitude et la phase de $U_R(t)$ soit $U_{R_m}$ et $\varphi_R$.
Or on sait que la loi qui lie la tension aux bornes d’une résistance et le courant qui la parcourt est la loi d’Ohm. Elle est également valable en régime alternatif.
Nous avons donc que :
$U_R(t)=R\times i(t)$
Par conséquent :
$U_R(t)=R I_m \cos(\omega t)$
Or on a posé $U_R(t)=U_{R_m} \cos(\omega t +\varphi_R)$
Pour la résistance c’est donc très simple, on obtient en identifiant amplitude et phase :
- $U_{R_m} =RI_m$
- $\varphi_R=0$
Remarque : identifier ça veut dire regarder ce qu’il y a devant le cosinus pour les deux expressions de $U_R(t)$ qu’on a et dire que ces quantités sont égales. De même pour ce qu’il y a dans le cosinus (l’angle).
On voit donc en particulier que $U_R(t)$ et $i(t)$ sont en phase : une résistance n’entraîne pas de déphasage !

Voici donc comment on trace les vecteurs $\vec{i}$ et $\vec{U_R}$ associés à $i(t)$ et $U_R(t)$ respectivement. Ils sont colinéaires et pointent dans la même direction : ils forment un angle de zéro degré. Et l’amplitude de $U_{R}$ est telle que $U_{R_m} =RI_m$. On trace d’abord le vecteur $\vec{i}$ puis on trace $\vec{U_R}$ en conséquence.
2.2 Condensateur
Faisons la même étude pour le condensateur. La question est donc, comment représenter le vecteur $\vec{U_C}$ associé à $U_C(t)$ la tension aux bornes du condensateur par rapport au vecteur $\vec{i}$ ?

Voici ce que nous savons sur un condensateur :
Soit $q$ la charge emmagasinée dans le condensateur. $q$ est une quantité d’électrons. Pour une tension donnée, plus la capacité $C$ du condensateur est grande, plus on peut y emmagasiner de charges :
$q=C\times U_C$.
Ici on est en régime alternatif, par conséquent $q$ et $U_C$ varient avec le temps. L’expression précédente devient donc :
$q(t)=C\times U_C(t)$.
Et comme un mouvement d’air correspond à un courant d’air, un mouvement de charges électriques signifie un courant électrique. On formalise cela mathématiquement par l’opérateur dérivé : si pendant un laps de temps très court on a une variation de charge, on a un courant électrique. Ce qui nous conduit à l’équation suivante :
$\displaystyle i(t)=\frac{dq(t)}{dt}$.
Pour ceux et celles qui veulent savoir ce qu’est une dérivée ou à quoi ça sert, j’ai écrit un article introductif de cette notion ici.
Parce que si vous ne connaissez pas les dérivées, vous n’allez pas aimer ce qui suit… 😆
Avant cela, restons un peu sur cette dérivée. En combinant les 2 équations précédentes on trouve que :
$\displaystyle i(t)=\frac{dq(t)}{dt}=C\frac{dU_C(t)}{dt}$.
Or nous avons supposé que l’on connaît le courant i(t) qui circule, on cherche donc $U_C(t)$. Il faut donc inverser la dérivée, et pour cela on utilise… l’intégrale… Désolé…
Si vous ne connaissez pas, admettez les deux lignes suivantes, c’est tout !
De l’expression précédente on déduit donc que :
$\displaystyle U_C(t)=\frac{1}{C}\int i(t)dt$, or $i(t)=I_m \cos(\omega t)$.
Par conséquent,
$\displaystyle U_C(t)=\frac{1}{\omega C} I_m \sin(\omega t)$
C’est bientôt fini. On sait que $\sin(x)=\cos(x-\frac{\pi}{2})$.
Par conséquent $\displaystyle U_C(t)=\frac{1}{\omega C} I_m \cos(\omega t-\frac{\pi}{2})$
Or $U_C(t)=U_{C_m}\cos(\omega t + \varphi_C)$
Par conséquent, on identifie amplitude et phase et on trouve que :
- $\displaystyle U_{C_m} =\frac{I_m}{\omega C}$
- $\displaystyle \varphi_C=-\frac{\pi}{2}$
Cette fois-ci, on voit que la tension aux bornes du condensateur et le courant ne sont plus en phase. La tension est en retard sur le courant de $\frac{\pi}{2}$ soit 90º.
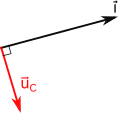
Une fois le vecteur $\vec{i}$ dessiné, on représente donc le vecteur $\vec{U_C}$ tel qu’il forme un angle droit avec $\vec{i}$,tourné de 90º dans le sens des aiguilles d’une montre (retard) et de longueur $\displaystyle \frac{I_m}{\omega C}$.
2.3 Bobine ou inductance
Finissons cette partie en traitant le cas des bobines :

La question est la même, connaissant $i(t)$, combien vaut l’amplitude de $U_L(t)$ et son déphasage par rapport à $i(t)$ ?
Ressortons nos formules sur les bobines. Nous savons que :
$\displaystyle U_L(t)=L\frac{di(t)}{dt}$ et $i(t)=I_m \cos(\omega t)$.
Cette fois-ci, on n’a « que » à calculer la dérivée de i(t) 😄😅
$\displaystyle U_L(t)=L\frac{di(t)}{dt}=-L\omega I_m \sin(\omega t)$
Or, nos formules de trigonométrie nous disent (au passage, ne les apprenez pas, retrouvez-les avec le cercle trigonométrique [1]) :
$-\sin x= \sin (-x)$ et $\sin (-x) = \cos(x+\frac{\pi}{2})$
Par conséquent $U_L(t)=\omega L I_m \cos(\omega t+\frac{\pi}{2})$
Or $U_L(t)=U_{L_m}\cos(\omega t + \varphi_L)$
Par conséquent, on identifie comme avant amplitude et phase et on trouve que :
- $U_{L_m} =I_m\omega L$
- $\displaystyle \varphi_L=+\frac{\pi}{2}$

Dans le cas d’une bobine, on trouve donc que la tension se trouve en avance de 90º sur le courant. Le module de la tension dépend de l’induction $L$ de la bobine et vaut $I_m\omega L$. On tracera donc le vecteur $\vec{U_L}$ associé à $U_L(t)$ à 90º du courant dans le sens inverse des aiguilles d’une montre.
Nous avons tout ce qu’il faut pour tracer un diagramme de Fresnel.
Cliquez sur le bouton pour charger le contenu de docs.google.com.
3 Le diagramme de Fresnel
Nous allons nous intéresser au circuit RLC série pour illustrer comment tracer un diagramme de Fresnel.
Voici le circuit en question :

Je pense que vous aurez compris pourquoi on l’appelle un circuit RLC. Et on le qualifie de série car les composants sont placés en série, non en parallèle.
J’ai utilisé les même notation que le paragraphe précédant pour les tensions aux bornes des composants.
3.1 Déterminons l’amplitude et le déphasage du courant
En traçant le diagramme de Fresnel on va trouver très facilement comment l’impédance totale du circuit va déphaser le courant et la tension.
Nous avons vu que chacun des éléments déphase la tension et le courant soit de -90º, 0º ou 90º. Combien vaudra la phase totale ? Que vaudra le courant ?
D’autre part, nous verrons que ce circuit agit comme un filtre. Imaginons que le générateur de tension soit le signal de la guitare et que l’on récolte la tension de sortie au niveau de la résistance. Quelle est la figure du gain de ce filtre ?
Le diagramme de Fresnel permet de répondre à toutes ces questions, sans avoir à utiliser le formalisme à première vue rebutant (mais ô combien utile) des nombres complexes.
Le circuit ci-dessus étant un circuit série, le courant est le même dans les 3 composants. Nous allons donc l’utiliser comme référence.
On trace donc le vecteur $\vec{i}$, par exemple horizontal pour plus de commodités. Puis on trace les vecteurs $\vec{U_R}$, $\vec{U_C}$ et $\vec{U_L}$ avec les déphasages qui leur correspondent. Voici ce que ça donne :
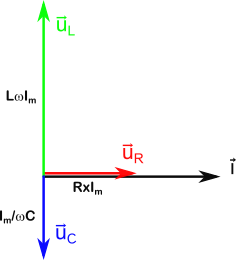
J’ai mis la longueur des vecteurs selon le calcul que nous avons vu dans le précédant paragraphe.
Pour trouver la tension totale $\vec{U}$ on va sommer les 3 vecteurs. On utilise la relation de Chasles, qui consiste à mettre l’origine du vecteur à sommer sur la pointe de l’autre vecteur. Voici ce que l’on obtient :
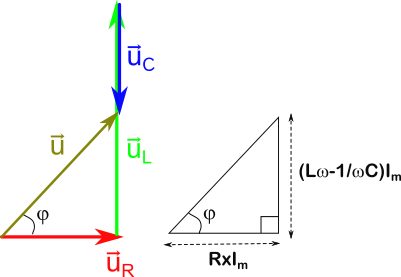
On obtient donc $\vec{U}$ tel que $\vec{U}=\vec{U_R}+\vec{U_L}+\vec{U_C}$. Il nous reste à calculer le module de $\vec{U}$ et son déphasage $\varphi$ avec $\vec{i}$.
Pour cela on remarque que $\vec{U}$ est l’hypothénuse d’un triangle rectangle dont on connaît la longueur des deux autres côtés. On utilise la formule de Pythagore pour trouver son module :
$U_m^2=(R\times I_m)^2+((L\omega – \frac{1}{\omega C})I_m)^2$
Donc $U_m^2=(R^2+(L\omega – \frac{1}{\omega C})^2)\times I_m^2$
Et donc $U_m=\sqrt{R^2+(L\omega – \frac{1}{\omega C})^2} I_m$
Or dans le présent circuit on connaît $U(t)$ car c’est la tension de notre générateur. C’est donc $i(t)$ que l’on cherche.
Par conséquent $I_m=\frac{1}{\sqrt{R^2+(L\omega – \frac{1}{\omega C}})^2}U_m$.
Et pour la phase on utilise la formule de la tangente qui dit que la tangente de l’angle est égale au rapport des longueurs du côté opposé du côté adjacent :
$\tan \varphi = \frac{(L\omega-\frac{1}{\omega C})I_m}{RI_m}$
On peut simplifier en haut et en bas par $I_m$ et en réécrivant un peu on trouve :
$\tan \varphi = \frac{1}{R}(L\omega-\frac{1}{\omega C})$
Donc $\varphi=\arctan(\frac{1}{R}(L\omega-\frac{1}{\omega C}))$.
On voit que le déphasage dépend de la pulsation, donc de la fréquence du signal donné par le générateur.
En résumé, pour le circuit RLC série :
- Nous avons posé $i(t)=I_m \cos(\omega t)$. Nous avons trouvé que $I_m=\frac{1}{\sqrt{R^2+(L\omega – \frac{1}{\omega C})^2}}U_m$.
- Le circuit impose un déphasage entre $i(t)$ et $u(t)$ qui vaut $\varphi=\arctan(\frac{1}{R}(L\omega-\frac{1}{\omega C}))$.
- L’impédance totale vaut $Z=\sqrt{R^2+(L\omega – \frac{1}{\omega C})^2}$.
- En général on cherchera $U_{R_m}$. Il suffit d’appliquer la loi d’Ohm et donc $U_{R_m}=R\frac{1}{\sqrt{R^2+(L\omega – \frac{1}{\omega C})^2}}U_m$.
3.2 Gain du circuit
Finalement, en définissant l’impédance totale du circuit $Z$ tel que $U_m=Z\times I_m$ (loi d’Ohm) on déduit que :
$Z=\sqrt{R^2+(L\omega – \frac{1}{\omega C})^2}$
Pour rappel, l’impédance c’est comme la résistance, mais pour un condensateur et une bobine. L’impédance exprime donc une résistance au passage du courant. On voit que l’impédance dépend aussi de la fréquence de l’onde. Par conséquent un condensateur et une bobine ne réagissent pas de la même manière aux basses fréquences et aux hautes fréquences.
L’impédance totale va nous servir à calculer le gain du circuit.
Imaginons, comme suggéré plus haut, pour concrétiser un peu plus tout cela que le circuit est inséré dans une pédale d’effet pour guitare. Le générateur est substitué par le signal de la guitare. La sortie est collectée au niveau de la résistance.
Le gain en tension est donné par ce qu’on reçoit divisé par ce qu’on donne. Par conséquent :
$\displaystyle G=\frac{U_{R_m}}{U_m}$
On a pris le rapport des amplitudes, mais on aurait pu prendre le rapport des tensions efficaces, cela revient au même.
En injectant la loi d’Ohm en haut et en bas :
$\displaystyle G=\frac{U_{R_m}}{U_m}=\frac{R\times I_m}{Z\times I_m}$
En remplaçant $Z$ par l’expression qu’on a trouvé et en simplifiant par $I_m$ on trouve :
$\displaystyle G=\frac{R}{\sqrt{R^2+(L\omega – \frac{1}{\omega C})^2}}$
Voyons comment évolue $G$ avec la pulsation $\omega$. On voit que le dénominateur de $G$ est minimum pour $L\omega – \frac{1}{\omega C}=0$
Posons $\omega_0$ tel que $L\omega_0 – \frac{1}{\omega_0 C}=0$.
Donc $L\omega_0 = \frac{1}{\omega_0 C}$
Et on trouve donc que $\omega_0^2=\frac{1}{LC}$,
donc $\omega_0=\frac{1}{\sqrt{LC}}$. On verra qu’en $\omega=\omega_0$ il se passe quelque chose d’incroyable !
Continuons.
En utilisant $\omega_0$ dans $G$ et après de légères simplifications on trouve pour $G$ :
$\displaystyle G=\frac{1}{\sqrt{1+\frac{L}{R}(\frac{\omega}{\omega_0} – \frac{\omega_0}{\omega})^2}}$
Que l’on peut réécrire en remplaçant la pulsation par la fréquence :
$\displaystyle G=\frac{1}{\sqrt{1+\frac{L}{R}(\frac{f}{f_0} – \frac{f_0}{f})^2}}$
Traçons $G$ en fonction de la fréquence $f$ :
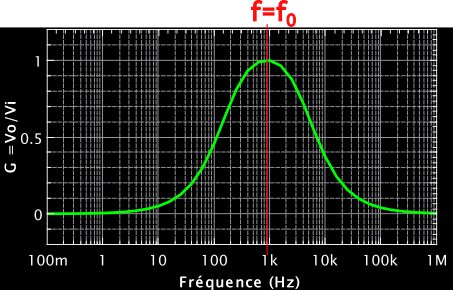
On observe une belle courbe de résonance, avec un beau pic en $f=f_0$ (ou $\omega=\omega_0$). C’est beau, n’est-ce pas ? 🙂
Sur le diagramme de Fresnel, on a résonance quand les flèches bleue et verte ont la même longueur. Les deux s’annulent et on ne trouve alors plus pour $\vec{U}$ qu’une contribution de la résistance. Le déphasage est nul, et l’impédance est minimale, d’où le pic (maximum de gain) !
Conclusion
Voilà, nous avons vu comment un diagramme de Fresnel nous aide en deux coups de crayons à prédire l’évolution d’un filtre. C’est donc un outil très utile.
J’espère que cet article vous aura éclairé sur l’intérêt du diagramme de Fresnel et comment le tracer.
Si vous avez des questions, en particulier sur les maths, n’hésitez pas à les poser en commentaire !
Références
[1] https://fr.wikipedia.org/wiki/Cercle_trigonom%C3%A9trique
