Dans l’article sur le filtre passe-bande rc nous avions vu qu’il est possible de créer un filtre passif qui ne laisse passer qu’une bande de fréquences. Ceci est très utile pour manipuler le signal et atténuer une plage de fréquence voulue. J’y avais donné la formule du gain directement, sans justification. Ici, je vous montre comment faire. Pour cela je vous montre une manière de calculer la fonction de transfert du circuit, ce qui vous servira d’exemple si vous souhaitez calculer la fonction de transfert de tout filtre RC du 2nd ordre à 2 cellules.
Nous allons rappeler quelques bases avant de s’attaquer au calcul. Ici je suppose que vous connaissez la loi des mailles, la loi d’Ohm et la loi des noeuds. Le niveau des maths est assez poussé, accrochez vous !
Je vous conseille de faire les calculs avec moi sur un papier, ça aide grandement à suivre.
Sommaire
1 Intérêt de tout ça
Pourquoi chercher la formule du gain ? Ou du déphasage ? Et bien quand on conçoit des circuits, ou quand on veut modifier une pédale d’effet, on peut y aller à tâtons, ou on peut tenter de prévoir le comportement du circuit.
Pour cela on peut utiliser un simulateur de type SPICE, c’est ce qu’on a fait dans l’article sus-mentionné sur le filtre passe-bande RC. Ceci requiert un ordinateur et un programme de simulation.
Ou si c’est possible on peut chercher une solution analytique (par le calcul) avec une feuille et un crayon. C’est ce qu’on se propose de faire ici.
Pour se convaincre que ça fonctionne bien, sur la figure suivante j’ai superposé le résultat du gain en fonction de la fréquence en sortie du circuit obtenu par la simulation (lignes continues) et obtenu par le calcul (symboles) pour différentes valeurs de la résistance de sortie :
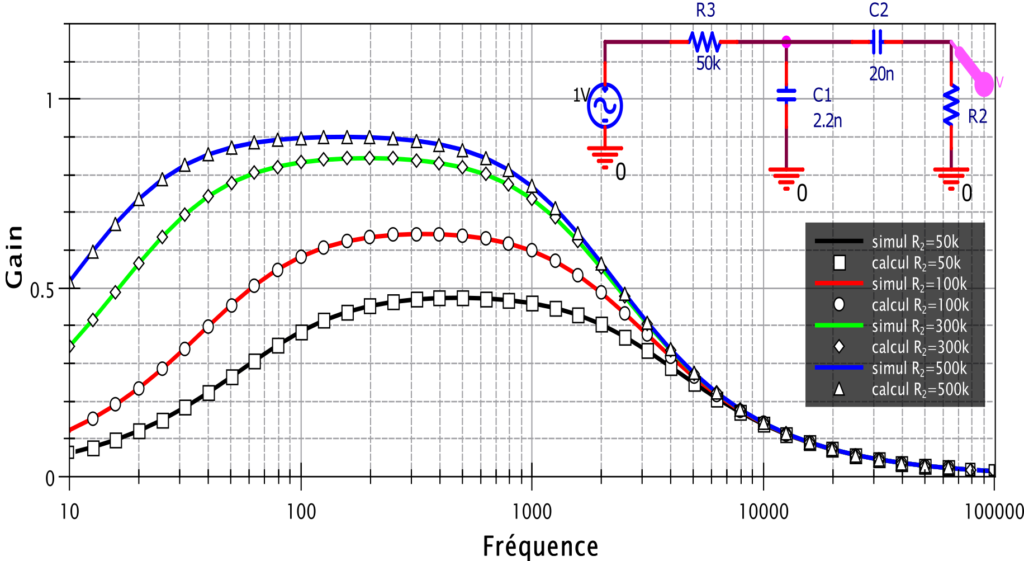
On constate un très bon accord entre les 2 méthodes.
Pour obtenir la formule du gain j’ai calculé la fonction transfert de ce filtre du 2nd ordre, je vais y revenir plus tard.
2 Rappels sur le signal
Le signal est une fonction qui varie dans le temps. Pour que notre calcul soit valable nous allons supposer que le signal est de type sinusoïdal. Appellons $V_e$ la tension d’entrée et $V_s$ la tension de sortie. Dire que $V_e$ est sinusoïdale se note ainsi mathématiquement :
$V_e=V_{e0}\sin(2\pi f t)$,
avec $V_{e0}$ l’amplitude, $f$ la fréquence et vous aurez reconnu le nombre $\pi$=3,14…
Cependant, en électronique on utilise plus souvent dans ce cas la pulsation $\omega$ que la fréquence $f$.
La fréquence $f$ et la pulsation $\omega$ sont reliées par :
$f=\frac{\omega}{2\pi}$
Par conséquent, on a pour $V_e$ :
$V_e=V_{e0} \sin(\omega t)$
En sortie, on va regarder pour une même fréquence que vaudra la tension de sortie $V_s$. Celle-ci aura probablement changé d’amplitude, que l’on notera $V_{s0}$. De plus, il est possible que $V_s$ sorte déphasée par rapport à $V_e$, c’est-à-dire que leur maxima ne vont pas forcément coïncider dans le temps.
Par conséquent on peut écrire $V_s$ :
$V_s=V_{s0}\sin(\omega t + \phi)$.
$\phi$ est le déphasage entre $V_s$ et $V_{e}$.
3 Rappel sur les notations complexes
Nous venons de voir que l’on définit le signal par une onde sinusoïdale. Celle-ci est définie par 2 paramètres :
- l’amplitude
- la phase
On a besoin des 2 pour définir l’onde. Sinon, c’est comme si vous disiez :
« On se voit à 11h à Barcelone sur la Rambla ! ».
Ce n’est pas suffisant, la Rambla est une longue avenue :
« Où sur la Rambla ? »
« Au croisement avec la rue Ferran ! »
Là oui. On se donne rendez-vous à un croisement, défini par 2 routes (non parallèles, oui).
Et bien pour décrire les ondes en mathématiques on a un outil très pratique, ce sont les nombres complexes car ce sont des nombres à 2 dimensions.
Le formalisme n’est pas forcément évident au début, mais c’est un outil qui rend ensuite la vie beaucoup plus simple pour ce qui est des calculs. Les filtres sont un exemple d’application parmi tant d’autres.
Ainsi, on définit l‘impédance complexe de chacun des composants passifs. Pour les composants qui nous intéressent, il y a juste à définir l’impédance complexe $Z_C$ du condensateur :
$Z_C=\frac{1}{jwC}$ avec $j$ le nombre complexe tel que $j^2=-1$.
Pour la résistance, l’impédance $Z_R$ est réelle donc :
$Z_R=R$.
4 Fonction de transfert des filtres passe-bas et passe-haut
La stratégie utilisée est de représenter les courants et tensions en représentation complexe et de transformer le circuit en son équivalent complexe. On résouds alors la loi des mailles, des noeuds etc… avec les nombres complexes. Puis on revient au réel pour déterminer le gain, le déphasage et la forme de l’onde en sortie.
Pour dire qu’une grandeur est complexe on met une barre en dessous.
Ainsi, $V_e$ en représentation complexe s’écrit $\underline{V_e}$.
On ne va pas s’en servir, mais on a donc :
$\underline{V_e}=V_{e0}e^{j\omega t}$
$\underline{V_s}=V_{s0}e^{j\omega t + \phi}$
On a la même chose pour le courant.
4.1 Mise en bouche : Fonction de transfert du filtre passe-bas
Nous avons déjà vu comment faire le calcul ici, mais pour s’échauffer revoyons le calcul de la fonction de transfert pour un filtre passe-bas.
Voici le circuit :
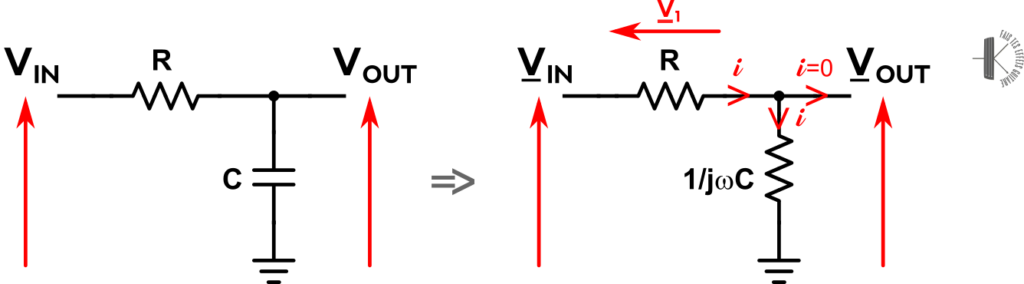
Sur la figure de gauche, on voit un circuit RC de type passe-bas. Il est composé d’une résistance et d’un condensateur. À gauche on a la tension d’entrée VIN et à droite on récolte la tension de sortie VOUT qui est la tension d’entrée modifiée en gain et en phase.
Rappelons que l’on mesure la tension par rapport à la masse.
À droite, j’ai représenté le même circuit en utilisant les impédances complexes. Cela fait apparaître $\frac{1}{j\omega C}$ l’impédance complexe du condensateur. Et les tensions deviennent des nombres complexes, c’est pour cela que j’ai mis une barre en dessous.
Fonction de transfert : définition
Ce qu’on cherche, c’est la fonction de transfert que l’on note $H$ (ou parfois $T$). $H$ est défini par le rapport entre la tension de sortie et la tension d’entrée. En gros, c’est ce qu’on gagne, divisé par ce qu’on donne. $H$ est une grandeur complexe qui dépend de la fréquence et du nombre complexe $j$ :
$$H(j\omega)=\frac{\underline{V}_{OUT}}{\underline{V}_{IN}}$$.
Une fois qu’on trouve $H$ on va en déduire facilement le gain G du circuit, il est simplement donné par le module de $H$. On peut aussi déduire le déphasage du circuit en calculant l’argument de $H$.
Pour trouver l’expression de $H$, on va utiliser la loi des mailles et la loi d’Ohm, j’ai donc ajouté le courant sur le circuit. On suppose qu’aucun courant ne sort du circuit (il y a donc un composant de très grande impédance en sortie). Cela signifie que rien ne charge le circuit en sortie.
Loi des mailles dans le circuit passe-bas
La loi des mailles nous permet d’obtenir une relation entre les tensions mises en jeu dans le circuit, à savoir $\underline{V}_{OUT}$, $\underline{V}_{1}$ et $\underline{V}_{IN}$. Il faut juste sommer les tensions en faisant attention au sens des flèches.
On trouve alors que :
$\underline{V}_{IN}=\underline{V}_{1}+\underline{V}_{OUT}$ : équation (1)
Utilisons aussi la loi d’Ohm
La loi d’Ohm donne la relation entre tension aux bornes d’un composant, courant qui le traverse et son impédance (ou résistance).
Aux bornes de R on a la loi d’Ohm normale :
$\underline{V}_{1}=R\times \underline{\textit{i}}$ : équation (2)
Et aux bornes de C, vu qu’on a une impédance complexe, on a la loi d’Ohm complexe :
$\underline{V}_{OUT}=\frac{1}{j\omega C}\times \underline{\textit{i}}$ : équation (3)
Expression pour le courant $\underline{\textit{i}}$
Injectons les équations (2) et (3) dans (1), on trouve :
$\underline{V}_{IN}=R\times \underline{\textit{i}}+\frac{1}{j\omega C}\times \underline{\textit{i}}$
Factorisons $\underline{\textit{i}}$ à droite :
$\underline{V}_{IN}= \underline{\textit{i}}\times (R+\frac{1}{j\omega C})$
Et on peut réécrire cette équation en isolant $\underline{\textit{i}}$ :
$\underline{\textit{i}}=\frac{\underline{V}_{IN}}{R+\frac{1}{j\omega C}}$
Voilà, super, on a une équation pour $\underline{\textit{i}}$.
Calcul de la fonction de transfert du circuit passe-bas
Reprenons l’équation (3) :
$\underline{V}_{OUT}=\frac{1}{j\omega C}\times \underline{\textit{i}}$
Et injections l’expression de $\underline{\textit{i}}$ dedans :
$\underline{V}_{OUT}=\frac{1}{j\omega C}\times \frac{\underline{V}_{IN}}{R+\frac{1}{j\omega C}}$,
que l’on peut réécrire :
$\underline{V}_{OUT}=\underline{V}_{IN} \times \frac{\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}}$.
Ce qui nous permet de trouver la fonction de transfert :
$$H(j\omega)=\frac{\underline{V}_{OUT}}{\underline{V}_{IN}}=\frac{\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}}=\frac{1}{1+j\omega RC}=\frac{1}{1+j\frac{\omega}{\omega_0}}$$
Avec $\omega_0=\frac{1}{RC}$ la pulsation de coupure du filtre. Elle nous permet de trouver la fréquence de coupure $f_0$, vue maintes fois dans ce site :
$$f_0=\frac{\omega_0}{2\pi}=\frac{1}{2\pi RC}$$
Gain du circuit
Finalement, le gain, qui est ce qu’on cherche, est donné par le module de la fonction de transfert. Par conséquent le gain est un nombre réel, il n’y a plus de $j$ dans la formule :
$G(\omega)=|H(j\omega)|=|\frac{1}{1+j\frac{\omega}{\omega_0}}|$
Donc :
$$G(\omega)=\frac{1}{\sqrt{1 +(\omega RC)^2}}=\frac{1}{\sqrt{1 +\left(\frac{\omega}{\omega_0} \right)^2}}$$
Déphasage
La fonction de transfert est un nombre complexe, elle apporte donc en plus du gain une 2e information qui est le déphasage de la tension de sortie par rapport à la tension d’entrée.
Notons $\phi$ ce déphasage, il se trouve en calculant l’argument de $H(j\omega)$ :
$$\phi(\omega)=\arg(H(j\omega))=-\arctan(\omega RC)=-\arctan\left(\frac{\omega}{\omega_0}\right)$$
4.2 Fonction de transfert du filtre passe-Haut
De la même manière on peut trouver la fonction de transfert du filtre passe-haut.
Voici le circuit à gauche et le circuit avec les impédances complexes équivalentes et les notations pour faire le calcul :
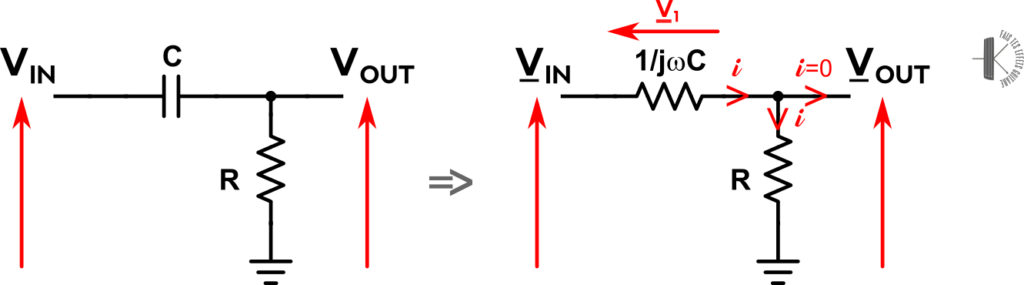
Je vous invite à faire le calcul vous même, il est très similaire à celui fait plus haut. On trouve pour la fonction de transfert :
$$H(j\omega)=\frac{\underline{V}_{OUT}}{\underline{V}_{IN}}=\frac{1}{1-j\frac{1}{\omega RC}}=\frac{1}{1-j\frac{\omega_0}{\omega}}$$.
Ce qui nous permet de trouver pour le gain G :
$$G(\omega)=|H(j\omega)|=\frac{1}{\sqrt{1 +\left(\frac{1}{\omega RC}\right)^2}}=\frac{1}{\sqrt{1 +\left(\frac{\omega_0}{\omega}\right)^2}}$$
Et pour le déphasage :
$$\phi(\omega)=\arg(H(j\omega))=\arctan\left(\frac{\omega_0}{\omega}\right)=\frac{\pi}{2}-\arctan\left(\frac{\omega}{\omega_0}\right)$$
5 Calcul de la fonction de transfert d’un filtre RC du 2nd ordre
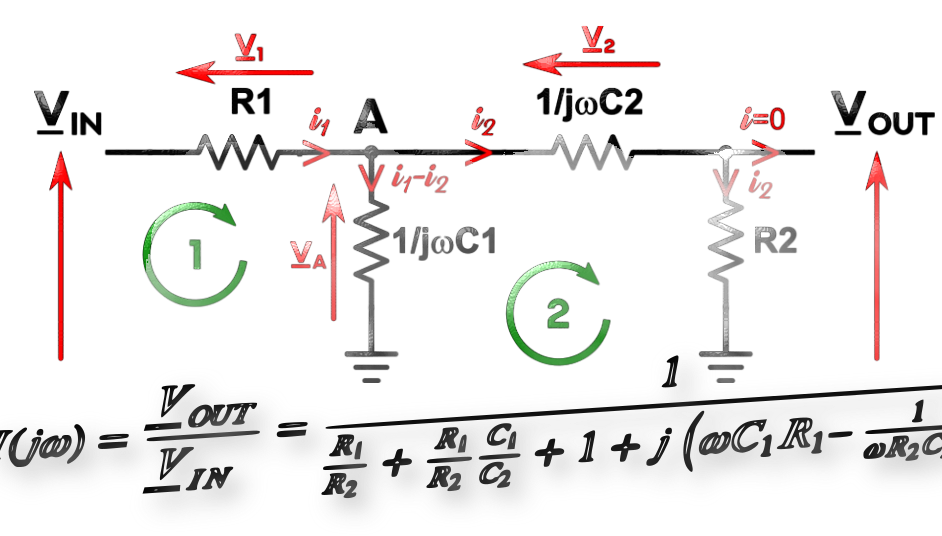
Voici le circuit auquel on s’était intéressé dans l’article à 2 cellules RC :
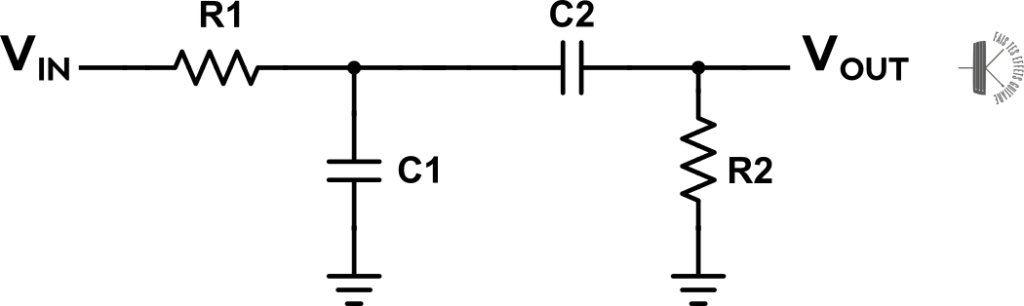
Grâce à l’échauffement sur les 2 filtres qu’on vient de faire, ça va passer comme une lettre à la poste !! 😀
On commence par reproduire le schéma en substituant les condensateurs par leur équivalent complexe :
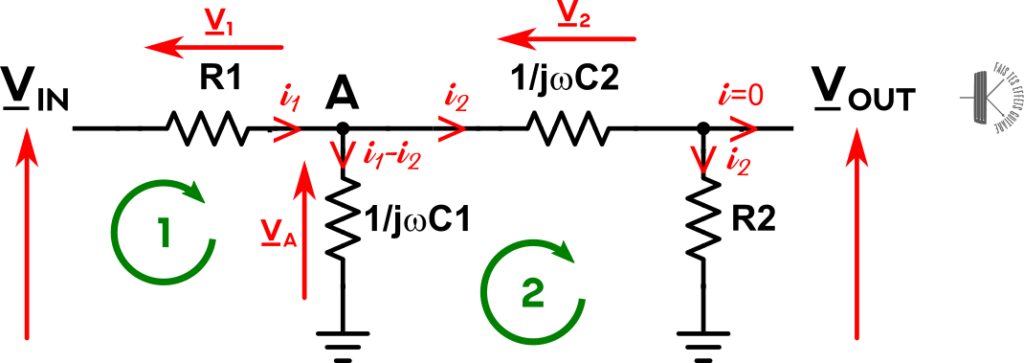
J’ai également fait figurer :
- les tensions : $\underline{V}_{IN}$, $\underline{V}_{OUT}$ et $\underline{V}_{A}$ la tension au point A,
- Les tensions aux bornes de R1, C1 et C2, respectivement $\underline{V}_{1}$, $\underline{V}_{A}$ et $\underline{V}_{2}$. Notez que la tension aux bornes de R2 est $\underline{V}_{OUT}$,
- Les courants $\underline{\textit{i}}_1$ et $\underline{\textit{i}}_2$. $\underline{\textit{i}}_1$ est le courant qui entre dans le circuit. En A il se divise, une partie nommée $\underline{\textit{i}}_2$ va vers C2, La différence $\underline{\textit{i}}_1-\underline{\textit{i}}_2$ se dirige vers C1. Notez que l’on suppose une grande impédance de sortie, donc tout le courant $\underline{\textit{i}}_2$ va dans R2,
- Les cercles verts 1 et 2. Ils servent à indiquer dans quelle maille on appliquera la loi des mailles.
NOTE : dans la suite des calculs je supprimerai les symboles de multiplication $\times$ inutiles (pour alléger l’écriture). Par exemple j’écrirai $\underline{V}_{OUT}=\frac{1}{j\omega C} \underline{\textit{i}}$ au lieu de $\underline{V}_{OUT}=\frac{1}{j\omega C}\times \underline{\textit{i}}$.
5.1 Loi des mailles en 1
Loi des mailles
Appliquons la loi des mailles dans la maille indiquée par le cercle vert nº1. Il suffit juste de sommer les tensions dans le sens de la flèche. Si la tension est en sens inverse, on met un signe « – » devant la tension.
On trouve donc que :
$\underline{V}_{IN}-\underline{V}_{1}-\underline{V}_{A}=0$.
Loi d’Ohm
Appliquons la loi d’Ohm en R1 :
$\underline{V}_{1}=R_1 \underline{\textit{i}}_1$
De même en C1 :
$\underline{V}_{A}=\frac{1}{j \omega C_1} (\underline{\textit{i}}_1-\underline{\textit{i}}_2)$
On peut donc réécrire l’équation de la loi des mailles que nous avons trouvé précédemment :
$\underline{V}_{IN}-\underline{V}_{1}-\underline{V}_{A}=0$
$\Rightarrow \underline{V}_{IN} = \underline{V}_{1}+\underline{V}_{A}$
$\Rightarrow \underline{V}_{IN} = R_1 \underline{\textit{i}}_1 + \frac{1}{j \omega C_1} (\underline{\textit{i}}_1-\underline{\textit{i}}_2)$. Appelons cette équation (1).
5.2 Loi des mailles en 2
Appliquons la loi des mailles dans le cercle vert nº2 :
$\underline{V}_{A}-\underline{V}_{2}-\underline{V}_{OUT}=0$.
De même que précédemment on remplace $\underline{V}_{A}$ et $\underline{V}_{2}$ en utilisant la loi d’Ohm. On peut réécrire directement la loi des mailles du cercle nº2 :
$\underline{V}_{A}-\underline{V}_{2}-\underline{V}_{OUT}=0$
$\Rightarrow \frac{1}{j \omega C_1} (\underline{\textit{i}}_1-\underline{\textit{i}}_2)-\frac{1}{j \omega C_2}\underline{\textit{i}}_2-R_2 \underline{\textit{i}}_2=0$.
Appelons cette équation (2). Nous y reviendrons.
5.3 Loi d’Ohm en sortie
En sortie du circuit, on peut appliquer la loi d’Ohm sur R2 :
$\underline{V}_{OUT}=R_2 \underline{\textit{i}}_2$.
Appelons cette équation (3).
5.4 Bidouillons (1), (2) et (3)
Nous avons 3 équations, nous allons les bidouiller pour faire disparaître les courants $\underline{\textit{i}}_1$ et $\underline{\textit{i}}_2$. Ceci va nous permettre d’obtenir une équation pour la quantité $\frac{\underline{V}_{OUT}}{\underline{V}_{IN}}$ qui est égale à la fonction de transfert $H(j \omega)$.
Cherchons une expression de $\underline{\textit{i}}_1$
Réécrivons l’équation (2), développons la parenthèse et mettons à gauche les termes qui contiennent $\underline{\textit{i}}_1$ et à droite les termes qui contiennent $\underline{\textit{i}}_2$ :
$\frac{1}{j \omega C_1} (\underline{\textit{i}}_1-\underline{\textit{i}}_2)-\frac{1}{j \omega C_2}\underline{\textit{i}}_2-R_2 \underline{\textit{i}}_2=0$.
$\frac{1}{j \omega C_1} \underline{\textit{i}}_1=\frac{1}{j \omega C_1} \underline{\textit{i}}_2+\frac{1}{j \omega C_2}\underline{\textit{i}}_2 +R_2 \underline{\textit{i}}_2$
Factorisons par $\underline{\textit{i}}_2$ tous les termes qui contiennent $\underline{\textit{i}}_2$ à droite :
$\frac{1}{j \omega C_1} \underline{\textit{i}}_1=\underline{\textit{i}}_2 \left( \frac{1}{j \omega C_1} +\frac{1}{j \omega C_2} +R_2 \right)$
Nous en déduisons en multipliant à gauche et à droite par $j \omega C_1$ :
$ \underline{\textit{i}}_1=\underline{\textit{i}}_2 \left(1+\frac {C_1}{C_2} + j\omega C_1 R_2 \right)$
Nous avons bien avancé car nous avons là une expression pour $\underline{\textit{i}}_1$. Dans celle-ci tous les termes à droite sont des paramètres (les R et les C) sauf $\underline{\textit{i}}_2$, qu’on éliminera ensuite grâce à l’équation (3).
Déduisons une expression de $\underline{V}_{IN}$
Mais pour l’instant, nous allons injecter l’équation que nous venons d’obtenir pour $\underline{\textit{i}}_1$ dans l’équation (1) (que nous n’avons pas utilisé jusque là). Ceci aura pour effet d’éliminer tous les $\underline{\textit{i}}_1$ de l’équation (1).
Rappelons (1) :
$\underline{V}_{IN} = R_1 \underline{\textit{i}}_1 + \frac{1}{j \omega C_1} (\underline{\textit{i}}_1-\underline{\textit{i}}_2)$
Puis injectons l’expression obtenue pour $\underline{\textit{i}}_1$ dedans :
$\underline{V}_{IN} = R_1 \underline{\textit{i}}_2 \left(1+ \frac {C_1}{C_2} + j\omega C_1 R_2 \right) + \frac{1}{j \omega C_1} \left(\underline{\textit{i}}_2 (1+ \frac {C_1}{C_2}+ j\omega C_1 R_2) -\underline{\textit{i}}_2\right)$
$\Rightarrow \underline{V}_{IN} = R_1 \underline{\textit{i}}_2 \left(1 + \frac {C_1}{C_2} + j\omega C_1 R_2 \right) + \frac{1}{j \omega C_1} \underline{\textit{i}}_2(1 + \frac {C_1}{C_2} + j\omega C_1 R_2 -1)$
On peut éliminer le $1-1$ dans la parenthèse et factoriser par $\underline{\textit{i}}_2$ à droite :
$\Rightarrow \underline{V}_{IN} = \underline{\textit{i}}_2 \left(R_1+ R_1 \frac {C_1}{C_2}+ j\omega C_1 R_1 R_2 + \frac{1}{j \omega C_2} +R_2\right)$
On avance bien. On a l’expression de $\underline{V}_{IN}$, on veut éliminer $\underline{\textit{i}}_2$ de l’équation et trouver $\frac{\underline{V}_{OUT}}{\underline{V}_{IN}}$.
Pour cela on va utiliser l’équation (3) qui était :
$\underline{V}_{OUT}=R_2 \underline{\textit{i}}_2$
Cette équation peut s’écrire comme cela :
$\underline{\textit{i}}_2=\frac{\underline{V}_{OUT}}{R_2}$,
car on veut isoler $\underline{\textit{i}}_2$.
Il ne reste alors plus qu’à injecter cette expression de $\underline{\textit{i}}_2$ dans l’expression de $\underline{V}_{IN}$ qu’on a trouvé :
$\underline{V}_{IN} = \underline{\textit{i}}_2 \left(R_1+ R_1 \frac {C_1}{C_2}+ j\omega C_1 R_1 R_2 + \frac{1}{j \omega C_2} +R_2\right)$
$\Rightarrow \underline{V}_{IN} =\frac{\underline{V}_{OUT}}{R_2} \left(R_1+ R_1 \frac {C_1}{C_2}+ j\omega C_1 R_1 R_2 + \frac{1}{j \omega C_2} +R_2\right)$
$\Rightarrow \underline{V}_{IN} =\underline{V}_{OUT}\left(\frac{R_1}{R_2} + \frac{R_1}{R_2} \frac {C_1}{C_2}+ j\omega C_1 R_1 + \frac{1}{j \omega R_2 C_2} +1\right)$
Or on sait que $\frac{1}{j}=-j$, c’est une propriété du nombre complexe imaginaire pur $j$. Par conséquent :
$\underline{V}_{IN} =\underline{V}_{OUT}\left(\frac{R_1}{R_2} + \frac{R_1}{R_2} \frac {C_1}{C_2}+1+ j\left(\omega C_1 R_1 – \frac{1}{ \omega R_2 C_2}\right) \right)$
5.5 Expression de la fonction de transfert
Et finalement on trouve pour la fonction de transfert :
$$H(j \omega)=\frac{\underline{V}_{OUT}}{\underline{V}_{IN}}=\frac{1}{\frac{R_1}{R_2} + \frac{R_1}{R_2} \frac {C_1}{C_2}+1+ j\left(\omega C_1 R_1 – \frac{1}{ \omega R_2 C_2}\right)}$$
Ouff, on y est. On a la fonction de transfert de notre filtre de 2nd ordre.
On reconnait d’ailleurs l’expression des fréquences de coupure du filtre passe-bas et du filtre passe-haut :
$\omega_1=2\pi f_{c1}=\frac{1}{R_1C_1}$
$\omega_2=2\pi f_{c2}=\frac{1}{R_2C_2}$
On peut réécrire l’expression de la fonction de transfert en utilisant ces notations :
$$H(j \omega)=\frac{\underline{V}_{OUT}}{\underline{V}_{IN}}=\frac{1}{\frac{R_1}{R_2} + \frac{\omega_2}{\omega_1}+1+ j\left(\frac{\omega}{\omega_1} – \frac{\omega_2}{\omega}\right)}$$
6 Gain $G$ et déphasage $\phi$ du circuit
On peut déduire le gain $G$ du circuit et le déphasage $\phi$ induit. Le gain du circuit c’est le module de $H$, et le déphasage c’est l’argument de $H$.
6.1 Gain
$$G(\omega)=|H(j\omega)|=\frac{1}{\sqrt{\left(1+\frac{R_1}{R_2} + \frac{\omega_2}{\omega_1}\right)^2+ \left(\frac{\omega}{\omega_1} – \frac{\omega_2}{\omega}\right)^2}}$$
Si au lieu de pulsation on parle de fréquence :
$$G(f)=\frac{1}{\sqrt{\left(1+\frac{R_1}{R_2} + \frac{f_{c2}}{f_{c1}}\right)^2+ \left(\frac{f}{f_{c1}} – \frac{f_{c2}}{f}\right)^2}}$$
On retrouve bien l’expression trouvée dans l’article précédent.
6.2 Déphasage
$$\phi(\omega)=\arg(H(j\omega)|)=-\arctan\left(\frac{\frac{\omega}{\omega_1} – \frac{\omega_2}{\omega}}{1+\frac{R_1}{R_2} + \frac{\omega_2}{\omega_1}}\right)$$
6.3 Discussion sur le gain
Nous avions vu dans l’article précédant qu’on observe une perte importante de gain comparée au circuit où les 2 cellules RC sont isolées (par exemple par un buffer).
Ceci est dû au terme $\frac{R_1}{R_2}$ dans le dénominateur de l’expression du gain. On peut calculer que dans le cas de 2 cellules indépendantes, ce terme disparaît, par conséquent le dénominateur est plus petit et donc le gain est plus grand.
7 Conclusion
Voilà, vous avez un exemple de calcul de fonction de transfert d’un filtre du 2nd ordre pour un circuit mettant en cascade 2 filtres RC du 1er ordre. Pour cela nous avons utilisé la loi des mailles, la loi d’Ohm et la loi des noeuds.
Nous aurions pu aller plus vite en utilisant le théorème de Thévenin, chose que je ferai dans un prochain article.
L’article est un peu ardu, surtout au niveau des maths. Si vous avez des questions n’hésitez pas à les poser en commentaires !

Bonjour,
Super article à digérer tranquillement.
Une petite erreur sur le schéma de fonction de transfert C2 a été symbolisé par une résistance
Bonjour Bill, oui c’est un peu velu, merci pour votre commentaire !
En effet C2 est symbolisé par une résistance, on fait ça lorsqu’on résout le circuit en utilisant les nombres complexes. La résistance, le condensateur et la bobine se symbolisent alors par une résistance et on parle d’impédance complexe, valant R, 1/jwC et jwL respectivement.