Nous avons croisé bien des fois la notion de filtre RC dans ce blog. Un filtre RC c’est juste la combinaison d’une résistance R et d’un condensateur C. Leur combinaison permet soit de filtrer les aigus de notre signal audio, soit les basses. En mettant donc 2 filtres RC à la suite, on va pouvoir filtrer à la fois les aigus et les basses. Je vous avais illustré cela « avec les mains » dans cet article, simulation à l’appui. Et je vous ai montré dans un autre article comment calculer la fonction de transfert du circuit et donc obtenir la réponse du circuit. On avait pour cela utilisé les lois de Kirchhoff (loi des mailles pour les tensions et loi des noeuds pour les courants) et la loi d’Ohm (relation entre courant et tension).
Les lois de Kirchhoff et la loi d’Ohm ont l’avantage d’être simple. Mais lorsque le circuit est velu, les calculs s’alignent à perte de vue. C’est déjà un peu ce qui se passe dans le cas du double filtre RC. Et bien souvent en électronique, ou en physique en général, on fait appel à des outils mathématiques au formalisme un peu compliqués qui, une fois intégrés permettent de résoudre des problèmes velus en quelques lignes. Ça, ça m’a toujours fasciné !
On a ça par exemple avec les nombres complexes. Ce sont des nombres à 2 dimensions. Ils ont été inventés un peu par « jeu » par les mathématiciens (j’exagère peut-être un peu). Leur application en physique n’est venue que plus tard [1]. En les appliquant aux problèmes faisant intervenir une oscillation périodique (phénomènes ondulatoires) comme c’est le cas en musique (une corde oscille), tout devient plus limpide et élégant. Oui, la complexité peut amener de la clarté. C’est ouf.
Et bien le théorème de Thévenin c’est ça, ça demande un peu de pratique, savoir transformer les sources de tension et de courant, calculer des résistances équivalentes. Mais une fois qu’on maîtrise l’application de ce théorème, tout se simplifie.
Ici je ne vais pas expliquer comment fonctionne le théorème de Thévenin, je vous réserve ça pour un prochain article.
Je veux juste montrer ici comment on obtient la résolution du double filtre RC par la méthode de Thévenin.
Sommaire
1 résolution du double filtre RC par la méthode de Thevenin
Voici pour rappel le circuit, assez simple, que l’on veut résoudre :
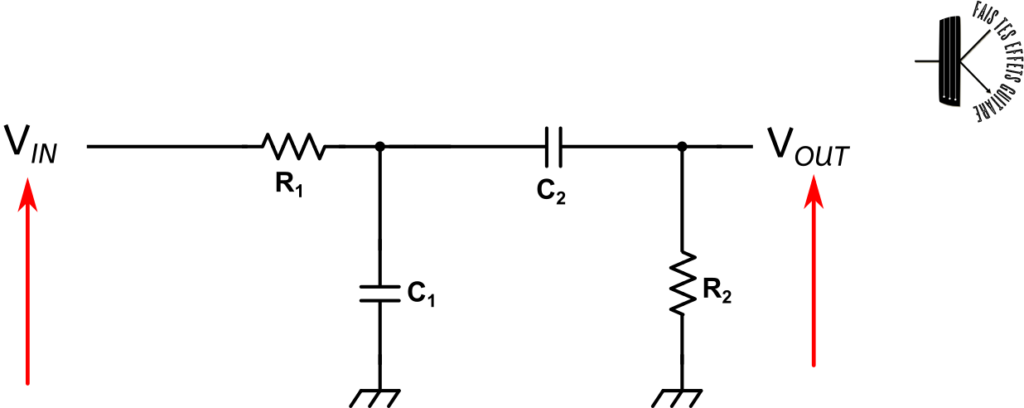
Ce circuit est constitué de 2 filtres RC en cascade. La répartition de la résistance et du condensateur détermine si la cellule RC laisse passer les aigus (filtre passe-haut) ou les graves (filtres passe-bas). Dans notre cas on a un filtre passe-bas suivi d’un filtre passe-haut, donc un filtre passe-bande.
La tension VIN est la tension d’entrée. C’est une tension dont l’amplitude dépend du temps. C’est tout simplement l’oscillation mécanique d’une corde de guitare par exemple, convertie en oscillation d’électrons par un engin qui s’appelle un microphone.
En sortie du circuit on obtient une tension VOUT qui oscille également, mais pour laquelle le filtre a atténué les vibrations à très hautes fréquences (les aigus) et les vibrations à très basse fréquence (les graves).
1.1 Remplaçons les composants par leur impédance complexe
Pourquoi je parle d’oscillation ? Vous me voyez venir… On va utiliser les nombres complexes, youpi ! ?
Ce qu’on fait c’est substituer la valeur des composants par leur impédance complexe qui, comme son nom l’indique, est un nombre complexe.
Dans notre cas, ceci n’affecte que le condensateur. Ce serait aussi le cas pour une bobine, oui, mais ici il n’y en a pas.
Ah, et une impédance, pour rappel c’est une juste résistance qui varie avec la fréquence. Voilà. J’en parle ici si cela vous intrigue.
Voici à quoi ressemble le circuit une fois les impédances complexes introduites :
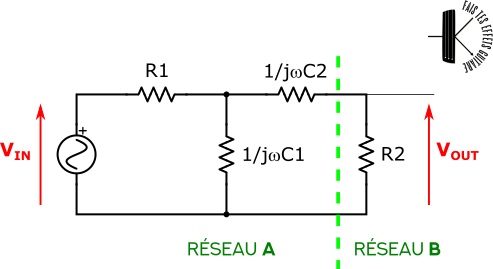
En gros j’ai juste remplacé les condensateurs par leur impédance complexe $\frac{1}{j\omega C}$. L’impédance d’une résistance ne dépend pas de la fréquence (ou de la pulsation $\omega$), on garde donc R.
Note : par convention je devrai mettre une barre sous les tensions, car ce sont des valeurs complexes aussi, mais je les omet pour la lisibilité du texte.
Sur ce dessin j’ai représenté la tension d’entrée VIN par une source de tension alternative sinusoïdale. La tension de sortie VOUT du circuit est la tension aux bornes de R2, comme avant. C’est elle qu’on cherche au final.
1.2 Stratégie utilisée dans la méthode de Thévenin
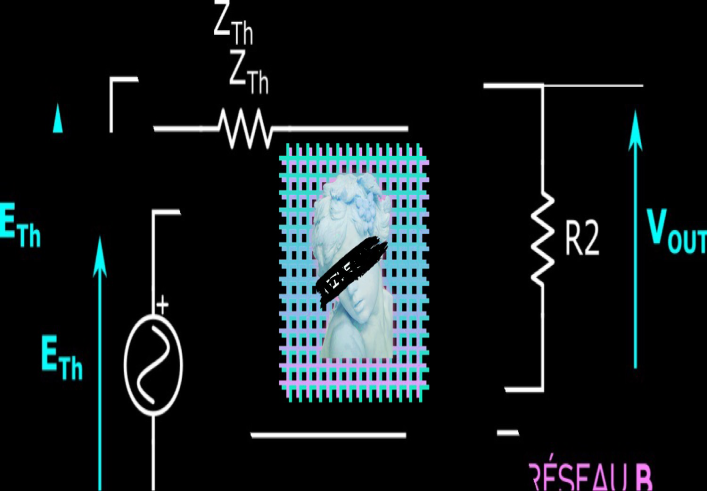
La méthode de Thévenin consiste à séparer le circuit en 2 sous-circuits. On s’intéresse à la tension en R2. La résistance R2 constituera donc un de nos 2 sous-circuits. Et le 2e sous-circuit, c’est le reste !
Ainsi, appelons réseau A le réseau à gauche de la ligne pointillée verte de la figure précédente et réseau B le circuit constitué par la résistance de charge R2.
Puis, on observe que dans le réseau A on a une source de tension et des impédances. On va chercher à remplacer tout ça par une source unique (dont la tension dépendra de VIN mais ne sera pas exactement VIN) et une résistance équivalente.
On appelle alors générateur de Thévenin de tension ETh la tension à vide du réseau A et résistance de Thévenin RTh la résistance équivalente du réseau A inactif.
Mais vu qu’on travaille avec des nombres complexes et que l’on note les impédances avec la lettre Z, on calculera ici une impédance équivalente de Thévenin que l’on notera ZTh [2].
1.3 Cherchons l’équivalent de Thévenin du réseau A : ETh et ZTh
1.3.1 Tension de Thévenin
On trouve la tension de Thévenin en calculant la tension à vide du réseau A. C’est-à dire qu’on fait fonctionner le réseau A, et on calcule la tension en sortie lorsqu’il n’y a rien de connecté :

Puisqu’il n’y a rien de branché en sortie, aucun courant généré par la source ne peut sortir, ni passer par C2.
Si aucun courant ne passe par C2, il y a 0 V à ses bornes. C2 est donc équivalent à un fil et on peut donc le sortir de notre problème, ce que je représente ici pour plus de visibilité :
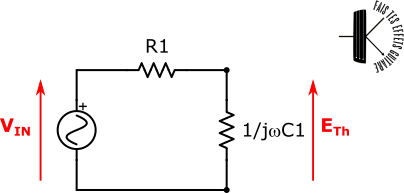
Et là c’est fastoche, on cherche ETh, tension aux bornes de C1. La tension totale vaut VIN et on a une chute de tension en R1 et en C1. C’est typiquement la configuration d’un pont diviseur de tension, il suffit d’appliquer la formule :
$$E_{Th}=\frac{\frac{1}{j\omega C_1}}{R_1 + \frac{1}{j\omega C_1} }V_{IN}=\frac{1}{1+j\omega R_1 C_1}V_{IN}$$
On obtient ainsi ETh en fonction des données du problème : VIN, R1, C1, donc c’est parfait.
ω est la pulsation (ou la fréquence à un facteur 2π près) et $j$ est le nombre complexe tel que $j^2=-1$.
1.3.2 Impédance de Thévenin
Cherchons maintenant l’impédance équivalente de Thévenin. Pour cela, la méthode consiste à laisser les sources inactives. On a dans le circuit une source de tension, la laisser inactive signifie la remplacer par un fil. Ainsi elle donne 0 V. C’est ce que je représente sur la figure suivante :

On obtient un circuit où R1 est parallèle à C1. Pour s’en convaincre j’ai redessiné la figure précédente comme cela :
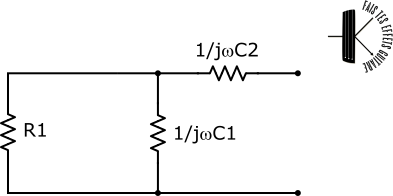
Redessinons ce circuit avec R1 et C1 en parallèle (j’utilise le symbole // pour signifier parallèle) :

Cette résistance parallèle est en série avec C2. On peut donc redessiner le circuit précédant avec un seul symbole d’impédance :
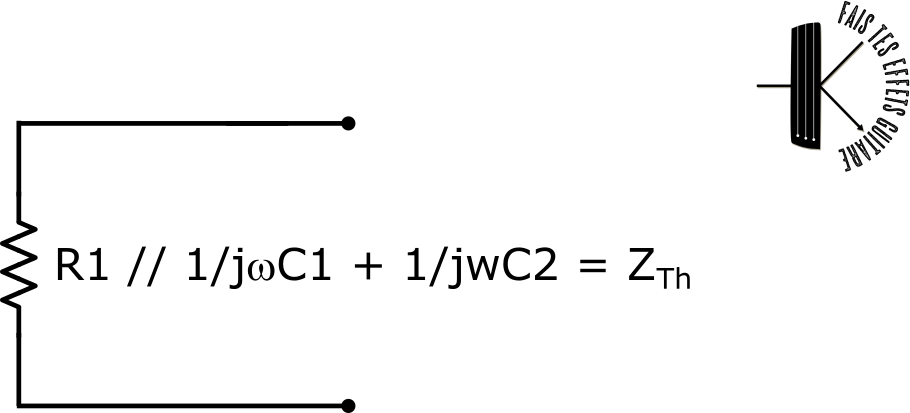
C’est l’impédance équivalente ZTh de notre circuit, ou impédance de Thévenin. Le raisonnement précédant nous aide à comprendre qu’il suffit de calculer l’impédance de R1 et C1 en parallèle et d’ajouter l’impédance de C2.
On obtient donc pour ZTh :
$$Z_{Th}=R_1 // \frac{1}{j\omega C_1} + \frac{1}{j\omega C_2} =\frac{R_1 / j\omega C_1}{ R_1 + 1/j\omega C_1}+ \frac{1}{j\omega C_2}$$
Par conséquent :
$$Z_{Th}=\frac{R_1}{ 1 + j\omega R_1 C_1}+ \frac{1}{j\omega C_2}$$
1.3.3 Équivalent de Thévenin du réseau A
Voilà ! On a trouvé l’équivalent Thévenin du réseau A, une source de tension ETh en série avec une impédance ZTh :

On peut maintenant brancher R2 au réseau A et calculer facilement ce qui nous intéresse depuis le début, VOUT. On se rend compte que comme précédemment on est dans le cas d’un pont diviseur de tension, on applique donc la formule pour trouver VOUT :
$$V_{OUT}=\frac{R_2}{R_2+ Z_{Th}}E_{Th}$$
Et on remplace ETh et ZTh par les expressions qu’on a trouvé plus haut :
$$V_{OUT}=\frac{R_2}{R_2+ \frac{R_1}{ 1 + j\omega R_1 C_1}+ \frac{1}{j\omega C_2}}\times \frac{1}{1+j\omega R_1 C_1}V_{IN}$$
On peut réarranger un peu tout :
$$ V_{OUT}= \frac{R_2}{R_2 (1 + j\omega R_1 C_1) + R_1 + \frac{1}{ j\omega C_2}(1+j\omega R_1 C_1)}V_{IN}$$
$$= \frac{R_2}{R_2+j\omega R_1 R_2 C_1 + R_1 + \frac{1}{j\omega C_2}+ \frac{R_1 C_1}{C_2}}V_{IN}$$
$$= \frac{1}{1+j\omega R_1 C_1 + \frac{R_1}{R_2} + \frac{1}{j \omega R_2 C_2} + \frac{R_1 C_1}{R_2 C_2}}V_{IN}$$
On peut mettre $j$ en facteur dans le dénominateur et on va poser $\omega_1=\frac{1}{R_1 C_1}$ et $\omega_2=\frac{1}{R_2 C_2}$. Ce sont les pulsations de coupure des 2 filtres (le passe-bas et le passe-haut). On obtient finalement pour VOUT :
$$V_{OUT}= \frac{1}{1+\frac{R_1}{R_2} + \frac{\omega_2}{\omega_1}+ j\left(\frac{\omega}{\omega_1} -\frac{\omega_2}{\omega}\right) }V_{IN}$$
Et là miracle, on retrouve la formule obtenue en utilisant les lois de Kirchhoff et d’Ohm de l’article sus-cité !!!
J’ai quand même bien détaillé, mais avec un peu de pratique on aurait pu y arriver en moins de lignes de calcul.
2 Résumé
Nous avons fabriqué un filtre passe-bande composé de 2 filtres RC en cascade. Nous voulons savoir quelle sera la forme du signal de sortie en fonction des paramètres du filtre qui sont la valeur des résistances R1 et R2 et les valeurs de capacité C1 et C2.
Pour cela, nous avons utilisé une technique d’analyse de circuit qui s’appelle le théorème de Thévenin. Le théorème de Thévenin dit qu’on peut remplacer tout réseau linéaire par un générateur de tension idéal en série avec une résistance.
Une des principales applications de ce théorème est la substitution d’une grande partie d’un circuit qui souvent peut être compliquée en un équivalent très simple : un générateur et une résistance.
Comme on l’a vu, le nouveau circuit permet de calculer ensuite très simplement la tension, le courant ou la puissance délivrée à une charge (la résistance R2 dans notre cas).
Notons finalement que nous avons utilisé le théorème de Thévenin en régime alternatif (AC). On a donc utilisé le concept d’impédance complexe.
Nous avons trouvé la fonction de transfert suivante :
$$H(j\omega)=\frac{V_{OUT}}{V_{IN}}= \frac{1}{1+\frac{R_1}{R_2} + \frac{\omega_2}{\omega_1}+ j\left(\frac{\omega}{\omega_1} -\frac{\omega_2}{\omega}\right) }$$
Si vous avez des questions ou des commentaires, n’hésitez pas à les écrire dans la zone « Laisser un commentaire » en dessous !!
Références
[1] https://fr.wikipedia.org/wiki/Nombre_complexe
[2] http://hyperphysics.phy-astr.gsu.edu/hbase/electric/acthev.html

On pourrait poursuivre l’exercice en faisant une représentation avec les fonctions de transfert
Oui tout à fait, diagramme de Bode etc…!